To measure the performance of the proposed method, experimental validation was conducted using two datasets described in
Section 2.1: the Vaihingen point cloud data from ISPRS and the Indianapolis_points_GTv1 dataset from STPLS3D. The former represents real data from a German region, while the latter is a simulation of an urban environment. These datasets differ in point cloud resolution, point spacing, and topographic and surrounding conditions.
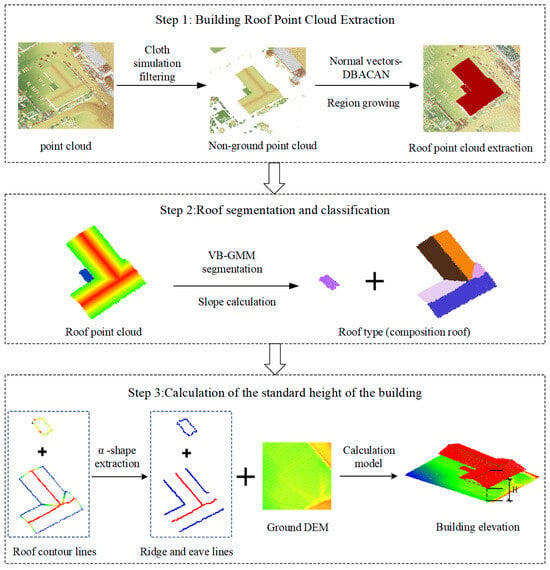
3.1. Building Roof Extraction
To enhance roof extraction performance, two building roof extraction experiments were conducted on the experimental areas from the two datasets (shown in the first column of
Figure 9). The neighborhood radius
Eps, minimum point threshold
, and dot product threshold
were configured for extraction. In this study,
Eps is set to 4,
to 60, and
to 0.9. The roof extraction results for the entire experimental area are shown in the second column of
Figure 9. Additionally, three smaller areas, labeled Area 1, Area 2, and Area 3, were selected from each dataset’s experimental area. These regions, marked by wireframes in the roof extraction results shown in
Figure 9, were chosen for detailed analysis.
As shown in
Figure 9, the method demonstrates strong overall performance in extracting roofs across large areas, with more complete extraction for individual roofs. It effectively captures most planar surfaces in the scene. Roofs with larger planar areas and more points are extracted more accurately. Simple flat and sloped roofs are captured precisely, even complex roofs show good performance. This result highlights the method’s effectiveness in handling diverse roof structures and processing complex point cloud data. In the Vaihingen dataset, extraction results were affected by varying levels of tree shading. Area 1 is impacted by surrounding trees, leading to missing and incomplete roof extractions. In contrast, Area 2 shows the best results due to fewer obstructions and larger, flatter roof surfaces. The accurate extraction of roof types in Area 3, despite the complexity and variation in its roof structures, further underscores the method’s adaptability in processing diverse architectural forms. Despite the method’s overall strong performance, roofs obscured by trees remain partially extracted due to missing point cloud data. In the STPLS3D dataset, the buildings are evenly distributed, trees are sparse, and the roof types are diverse, with many having complex structures. Although fewer non-ground points are removed by fabric simulation filtering, roof extraction remains relatively complete. In Area 1, the scarcity of trees and shading around the building, combined with a relatively flat roof surface, leads to a more complete extraction. In Area 2, the roofs are predominantly complex, with smaller areas and multiple planes. Despite this, the extraction is more effective due to reduced shading. In Area 3, the lack of shading, along with the larger and simpler roof structure, results in the best extraction performance.
While the extraction method presented in this paper generally performs well, it faces challenges in scenarios involving tree occlusions or significant height variations. In particular, when point cloud density is low or contains noise, the extraction completeness may be reduced. Overall, the method shows strong performance, especially in extracting large and simple building types, but there remains potential for optimization in more complex scenes.
3.2. Roof Surface Division
In order to achieve accurate segmentation of the roof surface, we adopt the VB-GMM method. This approach allows the model parameters to be adjusted for various segmentation outcomes and enhanced interpretability. In the experiment, the initial mixing coefficient
of the GMM is set to be uniformly distributed, meaning each component initially has equal probability. The coefficients automatically adjust during model training. The covariance matrix
is set as a multiple of the identity matrix, and the variational parameter is uniformly distributed, the GMM parameters are updated during variational inference. Roof segmentation is performed on the three experimental areas in both datasets, with the results shown in
Figure 10. Different colors represent the point clouds of distinct roof surfaces.
The segmentation results for the selected areas in the Vaihingen data, as shown in
Figure 10, are generally good. Various roof types are segmented accurately, including complex combined roofs. In Area 1, the roof types are primarily flat and sloped roofs, and the overall segmentation accuracy is better with precise boundary delineation for each plane. The roof types in Area 2 typically consist of fewer planes. The segmented surfaces are clear and complete, with strong differentiation between individual planes. Area 3 contains more complex and diverse roof types. Some edge point clouds were misclassified, resulting in slightly lower segmentation performance than in Areas 1 and 2. The three areas of complex roofs (I, II, III) in
Figure 10 consist of both sloped and flat roofs, segmented into eight, six, and seven planes, respectively. The segmentation results are ideal. The edge point clouds between planes are well categorized, and the planar structure is clearly differentiated, ensuring accurate segmentation while preserving the integrity of the roof structure. The results demonstrate that the method achieves high accuracy and stability when segmenting roof surfaces with complex structures.
In the STPLS3D dataset’s Indianapolis_points_GTv1 data, the segmentation results are better for regions with dense building distribution and complex roof structures. The segmentation of roofs with fewer surfaces is mostly complete, while roofs with more surfaces also show satisfactory results. The roofs in Area 1 are predominantly sloped, with numerous surfaces, making it difficult to accurately categorize the boundary point clouds between these surfaces. Although the roof structures in Area 2 are complex, their regularity allows for relatively accurate segmentation of each surface. Despite the increased complexity of roofs in Area 3, the overall segmentation performance is better. The segmentation of complex roofs (IV, V, VI), as marked by the black wireframe, which has up to 10 roof surfaces, is well executed, with each roof surface accurately categorized, ensuring the completeness of the planes. For roofs with many features and subtle differences, boundary segmentation at the intersections is less effective, and some edge point clouds are not accurately categorized.
Overall, the segmentation performance of this method across both datasets is highly satisfactory, particularly for large and flat roofs, where the results are outstanding. Even when handling roofs with complex structures, the overall performance remains excellent, although some boundary processing still requires optimization.
3.3. Building Height Calculation
In this experiment, the building height is calculated based on roof extraction and roof segmentation. The calculation focuses on determining the roof type and extracting ridge and eave lines. A slope threshold of 10% is used for roof classification: slopes below 10% are classified as Type I (flat roofs), slopes above 10% as Type II (sloped roofs), and buildings with both as Type III (combined roofs). For Type I (flat roofs) and Type II (sloped roofs), ridge and eave lines are extracted for sloped roofs, and only eave lines for flat roofs. The height of each section is calculated accordingly. For Type III combined roofs, the height of each section is calculated, with the maximum height taken as the final building height.
After segmentation, roof classification is performed for both datasets. The results are shown in the second row of
Figure 11, where blue represents Type I (flat roof), red represents Type II (sloped roof), and green represents Type III (combined roof). The building height results for each experimental area are shown in the third row of
Figure 10, rounded to two decimal places in meters. Yellow numbers indicate buildings taller than 9 m, while black numbers indicate buildings shorter than 9 m. The blue roof color gradient, ranging from light to dark, represents the gradual increase in building height from low to high. The results highlight representative areas.
As shown in
Figure 11, all three regions in the Vaihingen dataset feature various roof types, with fewer Type III combined roofs and a higher proportion of flat and sloped roofs overall. The calculated building heights show relatively small variations in the Vaihingen experimental area, with an overall even distribution. The minimum heights in the three regions are 4.22 m, 4.37 m, and 2.30 m, while the maximum heights are 12.65 m, 7.30 m, and 10.41 m, respectively. This suggests that in the Vaihingen experimental area, the building heights are relatively low, with minimal variation. The height differences are minor, reflecting a relatively uniform building structure across the region. In contrast, the experimental results for the STPLS3D dataset reveal distinct characteristics. Areas 1 and 3 consist of only Type I (flat roofs) and Type II (sloped roofs), with sloped roofs being more complex. No Type III combined roofs are present. The minimum building heights in the three regions of the STPLS3D dataset are 3.08 m, 5.08 m, and 3.35 m, while the maximum heights are 32.99 m, 32.84 m, and 24.33 m, showing a large height variation. Compared to the Vaihingen data, the STPLS3D region exhibits more pronounced variations in building height. This indicates that the STPLS3D dataset features a broader range of building types, likely including high-rise structures or buildings serving different functions.
In summary, the experimental results demonstrate the strong adaptability of this method for extracting various roof types and building heights. The Vaihingen data reveal relatively low and consistent building heights, while the STPLS3D data show highly varied building heights. Moreover, the method performs well in extracting roofs with complex structures, highlighting its effectiveness in handling complex scenarios.
3.4. Precision Evaluation
To assess the applicability and accuracy of the proposed method in this paper, a comparison between the automatic calculation and manual measurement results is conducted. The error between the two was analyzed using the method outlined in the literature [
34]. We calculate
R,
RMSE, and
MAE to evaluate the accuracy of building height calculations. The accuracy of the proposed method is evaluated using a least squares regression model. The formulas for calculating
R,
RMSE, and
MAE are as follows:
where is the number of data samples, represents the building heights calculated in this paper, represents the building heights measured manually, and is the mean value of the heights calculated in this paper.
The difference between the manual measurements and the calculated results from this paper is recorded as an error. The building height error for the three areas in the Vaihingen and STPLS3D regions is shown in
Figure 12 and
Figure 13, respectively. The roof colors, from light to dark, represent the error range, with lighter colors indicating smaller errors and darker colors indicating larger errors in the height calculations.
The results show that the proposed method has high accuracy with relatively small errors. In the Vaihingen region, the maximum errors for the three experimental areas are 1.92 cm, 1.72 cm, and 1.80 cm, while the minimum errors are 0.65 cm, 0.64 cm, and 0.44 cm, respectively. For the STPLS3D region, the maximum errors are 1.79 cm, 1.45 cm, and 1.01 cm, while the minimum errors are 0.11 cm, 0.11 cm, and 0.10 cm, respectively. Overall, the errors in the building height calculations across both datasets are small (less than 2 cm), demonstrating the reliability and applicability of the proposed method. The error in the STPLS3D dataset is smaller compared to the Vaihingen dataset, mainly due to the higher density of point cloud in STPLS3D. The closer spacing of points in STPLS3D results in higher accuracy in its experimental outcomes compared to Vaihingen.
The R, RMSE, and MAE between the manually measured and automatically calculated building heights are computed using the least squares regression model for both datasets. The results of regions and roof types are shown in
Table 1 and
Table 2, respectively. As shown in
Table 1, the number of buildings in the three areas of the Vaihingen dataset varies slightly. However, the R values for all areas are close to 1, indicating a strong correlation between the automatically calculated building heights and actual measurements, with an overall error of less than 2 cm. Among the three areas, Area 1 shows the largest maximum error, RMSE, and MAE, with an RMSE of 1.18 cm, indicating a relatively large height calculation error in this area. Nevertheless, the RMSE and MAE remain within acceptable limits, indicating that the overall building height calculation accuracy in the Vaihingen area is high. In the STPLS3D dataset, the buildings are uniformly distributed, and the R values are approximately 1, indicating high accuracy in height calculations. The RMSE values are 0.82 cm, 0.70 cm, and 0.76 cm, and the MAE values are 0.57 cm, 0.49 cm, and 0.68 cm, respectively. Area 1 exhibits the largest difference between maximum and minimum errors, resulting in the highest RMSE. Conversely, Area 2 has the highest computational accuracy, with the smallest RMSE and MAE.
The calculation results, categorized by roof type, and the corresponding error and accuracy evaluations are presented in
Table 2. From
Table 2, the number of roofs across the three types in the Vaihingen data varies significantly, with Type III containing only five samples. However, Type III exhibits the smallest RMSE and MAE, suggesting that the computational method offers stability and accuracy when handling complex roof structures. The RMSE and MAE for Type I and Type II are slightly higher, but remain within a narrow range, with the maximum error not exceeding 2 cm, validating the method’s reliability across different roof types. In the STPLS3D dataset, the maximum and minimum errors for different roof types vary significantly, especially for Type II, which has a maximum error of 1.79 cm and a minimum error of 0.11 cm, reflecting notable height variations. Nevertheless, the RMSE and MAE remain low, particularly for Type III, with an RMSE of 0.61 cm and an MAE of 0.60 cm, demonstrating the method’s adaptability in this dataset.
In summary, the automatic building height calculation method proposed in this paper demonstrates high accuracy, both when assessing building heights by region and by roof type. In both regions with significant building height variations and roof types of varying complexity, calculation errors remain within 2 cm, and R values are close to 1. The observation demonstrates that the calculated building heights are close to the measured values, confirming the applicability and reliability of the proposed method.
Source link
Yuehuan Wang www.mdpi.com