A Hybrid Mamba–CNN UNet for Infrared Small Target Detection

1. Introduction

Due to the ability of infrared sensors to capture infrared radiation emitted or reflected by objects and convert it into visible images, infrared small target detection is widely applied across military reconnaissance, security surveillance, forest fire prevention, and assistance systems for night driving [1], contexts in which target identification in low-light or dark environments is required [2]. Infrared small target detection has advantages over radar and visible light detection, such as good concealment, strong penetration, and a passive detection mechanism. However, despite these many advantages, infrared small target detection also faces some challenges in practical applications. Firstly, due to the long detection distances and actual sizes of the small targets involved, these small targets are represented by very few pixels in the images, complicating effective feature extraction. Additionally, the signal-to-noise ratio (SNR) is often very low because the signals from small targets are typically weak and easily masked by background noise. These difficulties affect the accuracy of detection. There are high requirements for real-time performance in infrared small target detection scenarios, especially in applications such as vehicle night vision systems, where potential hazards need to be identified quickly and accurately in dynamic scenes, leading to high demands in terms of the processing speed of the algorithms. On these bases, further developments in infrared small target detection (ISDT) are pivotal [3,4].

The traditional methods for detecting small targets in infrared imagery have followed a model-driven approach, in which mathematical models for problem-solving are established based on theory. These include several representative methods. Filter-based methods [5,6,7,8,9] enhance the target features and suppress the background through the filter design, thereby improving the signal-to-noise ratio. Methods that utilize local contrast mechanisms [10,11,12,13,14] increase the intensity of weak signals to enhance the contrast, thus highlighting the targets. Methods involving the decomposition of sparse and low-rank tensors

The application of deep learning to the field of infrared detection of weak and small targets has become a popular direction within the research. Unlike the traditional model-driven methods, neural networks are data-driven and offer many advantages: end-to-end learning without the need for manually designed features, strong generalization, hardware acceleration, parallel processing capabilities, high precision, and robustness. Given their suitability for feature encoding and decoding, CNN networks excel at extracting hierarchical feature information. Their weight-sharing design makes them particularly good at handling translation invariance and recognizing local features. Within this field, the concept of target segmentation using a UNet has inspired many representative works. For example, Wang et al. [15] utilized the concept of adversarial learning in Generative Adversarial Networks (GANs) to achieve a balance between the two subtasks of missed detections (MDs) and false alarms (FAs). With each network focused on one subtask, task flexibility is improved. Weak and small target detection is also aided using semantic segmentation techniques, such as using a symmetrical encoder–decoder structure. Dai et al. published several important works in this vein. ACMnet [16] employs asymmetric contextual modulation, integrating low-level texture information and high-level semantic information to alleviate the issue of low-level feature loss. ALCnet [17] uses the method of cyclically shifting the feature maps, thus surpassing the limitations of the receptive field of the convolutional kernels to facilitate long-distance contextual interactions. Li et al. proposed DNAnet [18], which enhances the robustness of the network through the dense, nested UNet architecture to promote interaction and fusion of the features between layers. Wu et al. introduced UIUnet [19], in which the feature integration in the original UNet was improved by replacing its feature-extraction blocks with residual U-blocks. In addition, to ensure sufficient training data are available and promote the development of the field, certain research teams have provided public and open-source infrared target detection datasets [15,16,18,20,21].

Nevertheless, where CNNs are applied within this domain, the challenge of lower-level feature loss arises, leading to poorer performance in deeper networks and a tendency towards overfitting. Transformers, on the other hand, are increasingly popular neural network architectures that have also been successfully applied to image processing despite being conceived for natural language processing purposes initially. For example, Vision Transformers (ViTs) have been used for image recognition [22], the Swin Transformer serves as a universal backbone network in various visual tasks [23], and they have also found extensive applications for processing remote sensing images [24]. Unlike CNNs, transformers treat images as a sequence of patches instead of naturally considering their spatial hierarchical structures. They are better at capturing global information, and the introduction of global dependencies somewhat mitigates the issue of lower-level information being diluted by higher-level information, thus addressing the aforementioned shortcomings of CNNs. Many studies have explored the use of hybrid transformer–CNN network architectures in image segmentation tasks [25,26,27,28]. IAAnet, proposed by Wang et al., employs a transformer encoder to model the attention relationships within the target regions, utilizing a range from coarse to fine [29]. Despite their improved capacity to handle long-range dependencies, transformers typically incur high computational costs; as the self-attention mechanism grows quadratically with the size of the input, high-resolution image processing requires a sharp increase in computational complexity.

Recently, state space models (SSMs), particularly the Structured State Space Column Model (S4), have served as an effective backbone for constructing deep networks, achieving optimal performance in analyzing continuous, long sequences [30]. Mamba further improves upon S4 by introducing a selection mechanism that allows the model to choose information that is relevant to the input. Where it has been coupled with a hardware-aware implementation, Mamba has surpassed transformers in tackling dense modalities such as language and genomics. Moreover, state space models have shown promising results in visual tasks, including image and video classification [31,32]. In the field of infrared small target detection, Chen et al. proposed MIM [33], which uses a nested Mamba model with inner and outer layers to extract the global information ingeniously. Given that image patches and image features can also be considered sequences [22,23], we have been inspired to explore the potential to use the Mamba model to enhance the capability of CNNs to model long distances.

Thus, we designed HMCNet, a UNet that integrates a hybrid Mamba–CNN module. This network adopts the symmetric encoder–decoder design within the UNet, where feature layers of the same depth in the encoder and the decoder are connected through skip connections to facilitate context interactions. For each feature extraction block, we designed a Hybrid Vision State Space Module (HY-SSM) to integrate the convolutional branch and the Mamba branch. The convolutional branch uses multi-scale hybrid modules and focus-aware modules to increase the receptive field and enhance the local feature extraction, while the Mamba branch imbues the model with efficient global attention capabilities. Thus, the model’s design not only retains the power of CNNs in feature extraction from local receptive fields but also introduces more computationally friendly global attention modules. Our experiments on both public and private datasets show this method’s effectiveness in achieving the best results and a faster inference speed.

The main contributions of this work can be summarized as follows:

We propose HMCNet: a UNet that combines a CNN and the Mamba backbone network for small target segmentation using infrared, unifying the characteristics of CNNs in enhancing the local receptive fields and the advantages of state space models in terms of their low computational complexity and linear scalability.
We designed a multi-scale fusion block (MSFB) and a focus-aware block (FAB). These modules enhance the extraction of the local features while increasing the local receptive field.
The experimental results on the public IRSTD-1k dataset and the MISTD dataset we built indicate that the method proposed achieves superior detection accuracy and retains high-speed inference capabilities, thus validating the rationality and effectiveness of this research.

3. Methods

3.1. Preliminaries

3.1.1. The State Space Model

State space models (SSMs) [53] are utilized to depict the representation of the state of a sequence at various time steps and predict its subsequent state based on the input. They are commonly employed for linear time-invariant systems. A one-dimensional input signal

x (t) \in R

is transformed into the predicted output signal

y (t) \in R

through a hidden state

h (t) \in R^{N}

. A differential equation representing the process above is as follows:

$\begin{matrix} \{\begin{matrix} h^{'} (t) & = A h (t) + B x (t) \\ y (t) & = C h (t) + D x (t) \end{matrix} \end{matrix}$

(1)

where $A \in R^{N \times N}$ is the state matrix, while $B \in R^{N \times 1}$ and $C \in R^{N \times 1}$ represent the projection parameters. The skip connection term $D \in R$ can be regarded as a residual connection; thus, the SSM does not necessarily need to include item D.

3.1.2. Discretization

Given that they are continuous-time systems, challenges are faced in integrating SSMs with modern deep-learning frameworks designed for discrete-time operations. They need to be discretized to run efficiently on hardware, allowing deep-learning algorithms like gradient descent and backpropagation to be applied. Discretization also aligns with the discrete nature of real-world data, and it enables the model’s complexity to be adjusted by varying the time steps to balance its computation and accuracy.

For the input vector

x_{k} \in R^{L \times D}

sampled from a signal of length L, we discretize the continuous parameter matrices A and B into

\bar{A}

and

\bar{B}

by introducing the time scale parameter

Δ

according to the zero-order hold principle [54]. The final results of discretization are as follows:

$\begin{matrix} \{\begin{matrix} h_{k} & = \bar{A} h_{k - 1} + \bar{B} x_{k} \\ y_{k} & = C h_{k} \\ \bar{A} & = e^{Δ A} \\ \bar{B} & = (e^{Δ A} - I) A^{- 1} B \\ \bar{C} & = C \end{matrix} \end{matrix}$

(2)

where B, $C \in R^{D \times N}$ , and $Δ \in R^{D}$ . We can only use first-order Taylor series to approximate $\bar{B}$ :

$\bar{B} = (e^{Δ A} - I) A^{- 1} B = (Δ A) {(Δ A)}^{- 1} Δ B = Δ B$

(3)

Therefore, we can transform the expressions above into the following matrix multiplication form:

$\begin{matrix} \{\begin{matrix} \bar{K} & = (C \bar{B}, C \bar{A B}, \dots C \bar{A^{L - 1} B}) \\ y & = x \bar{K} \end{matrix} \end{matrix}$

(4)

where $K \in R^{L}$ represents the convolution kernel, which we can then integrate into the neural network.

3.2. Architecture

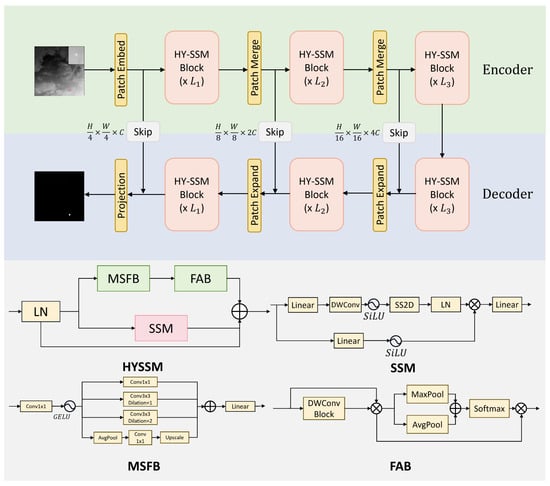
Figure 1 illustrates the overall architecture of HMCNet. Overall, HMCNet consists of a patch embedding layer, an encoder, a decoder, a projection layer, and skip connections between the encoder and the decoder. We adopted a symmetric structure. The patch embedding layer divides the input image

x \in R^{H \times W \times 3}

into non-overlapping patches of size

4 \times 4

and then maps the image dimensions to C, where we set C to 32 by default. This process results in the embedded image

x^{'} \in R^{\frac{H}{4} \times \frac{W}{4} \times C}

. Subsequently, before the patches are input into the encoder for feature extraction, we normalize the input patches using layer normalization [55]. Both the encoder and the decoder consist of three stages, with patch merging operations applied at the end of the first two stages to reduce the height and width of the input features while increasing the number of channels. For example, the output feature map of the first HY-SSM block has dimensions of

\frac{H}{4} \times \frac{W}{4} \times C

. After the first patch merging operation, its dimensions change to

\frac{H}{8} \times \frac{W}{8} \times 2 C

. We use [2, 2, 2] HY-SSM blocks in the three stages, with the channel count for each stage being

[C, 2 C, 4 C]

The structure of the decoder is very similar to that of the encoder. The output of the SSM block from the last stage enters the decoder. While the output of each block undergoes patch merging in the encoder, in the decoder, a patch expanding operation is applied to the output of each block to halve the number of feature channels and increase its width and height. We use SSM blocks at a ratio of [2, 2, 2], with the channel counts for each stage being [4C, 2C, C], respectively. Subsequent to the processing of the decoder, the final projection layer is used to restore the size of the feature map to the same dimensions as those of the input image, resulting in the final segmentation image.

In addition to the overall structure of the encoder and the decoder mentioned above, we also used skip connections between the encoder and the decoder. To maintain a simple network structure and reduce the number of parameters, we used an addition operation.

3.3. The HY-SSM Block

The HY-SSM module is composed of two branch modules: one is the SSM module branch derived from Vmamba [50], and the other is the CNN branch, consisting of a multi-scale feature fusion block (MSFB) and a focus-aware block (FAB). The input feature map first undergoes layer normalization and is then split into the aforementioned two branches for processing, after which the outputs of the two branches are fused with the input feature map.

The CNN branch consists of a multi-scale feature fusion block (MSFB) and a focus-aware block (FAB). The MSFB module consists of a 1 × 1 convolutional layer, a GeLU [56] activation layer, and an Inception module. The Inception module comprises four branches: a 1 × 1 convolutional layer branch, two 3 × 3 convolutional layer branches with dilation coefficients of 1 and 2, and an average pooling branch. After the four branches are added together, they pass through a linear layer to obtain the output of the MSFB module. The output of the FAB module is generated by sequentially merging two attention branches with the main branch. The first spatial attention branch obtains feature map attention in the width and height dimensions via a depthwise separable convolutional block. The depthwise separable convolutional block consists of a 3 × 3 depthwise separable convolutional layer, a batch normalization layer, and a GeLU activation layer. The second channel attention branch combines average pooling and max pooling of the feature maps, followed by passing them through a SoftMax layer. The two attention branches are sequentially multiplied and merged with the feature map to produce the final output.

The SSM module branch uses SiLU [57] as the activation function. The SSM module is divided into two branches, one of which consists of only two layers—a linear layer and an activation function. The other branch comprises a linear layer, a depthwise separable convolutional layer, and an activation function, after which the input enters the 2D-Selective-Scan (SS2D) module for feature extraction. Subsequently, the extracted features undergo layer normalization and are multiplied element-wise with the output of the first branch to integrate the features from both paths. Finally, the features from the two branches are mixed using a linear layer. The outputs of the two modules are then combined with the original input content to finally generate the output of the HY-SSM module.

The SS2D module is the core module in Mamba and consists of three parts: a scan-expanding operation, an S6 module, and a scan-merging operation. As shown in Figure 2, the scan-expanding operation unfolds the input feature map into independent sequences in four different directions. The scanning strategies in these four directions ensure that each element can interact with the previously scanned samples, thereby integrating information from all the other directions and involving a global receptive field without increasing the linear computational complexity. The S6 module, derived from the Mamba model [53], introduces a selection mechanism on the basis of S4 [30], enhancing its ability to distinguish and retain useful information while filtering out useless information. The S6 module is used to perform feature extraction on the unfolded feature map sequences, obtaining features from the sequences in different directions, and finally, to merge the output sequences through a scan-merging operation to produce an output feature map with the same dimensions as the input feature map.

Assuming the feature input into the SS2D module is z, the feature output can be represented as follows:

$\begin{matrix} \begin{matrix} z_{i} & = e x p a n d (z, i) \\ \bar{z_{i}} & = S 6 (z_{i}) \\ \bar{z} & = m e r g e (\bar{z_{1}}, \bar{z_{2}}, \bar{z_{3}}, \bar{z_{4}}) \end{matrix} \end{matrix}$

(5)

Here, $i \in {1, 2, 3, 4}$ represents the four scanning directions, and expand() and merge() represent the scan-expanding and scan-merging operations, respectively. A more in-depth explanation of this concept is provided in [50].

3.4. The Loss Function

When segmenting small targets in infrared, the targets occupy a very small proportion of the images, while the background takes up a large proportion. The number of negative background samples is several orders of magnitude greater than the number of positive target samples, leading to a severe imbalance between the number of positive and negative samples. This imbalance predisposes the classifier to make predictions for the majority class and ignore the minority class, thereby reducing the overall performance of the model and its ability to make predictions for the minority class. To alleviate this imbalance in the samples, we use the SoftIoU loss function and the focal loss function.

Focal loss (FL) [58] is a loss function used to address imbalances between classes, which are particularly prevalent in object detection and image segmentation tasks. The formula for focal loss is as follows:

$F L = - α_{t} {(1 - p_{t})}^{γ} l o g (p_{t})$

(6)

where $p_{t}$ is the probability predicted by the model; $α_{t}$ is the balancing factor for the samples, which adjusts the proportions of different samples; and $γ$ is a tunable parameter for balancing the importance of samples that are easy and hard to classify. When the probability $p_{t}$ approaches 1, a sample is considered easy to classify, and it is assigned a smaller weight. Conversely, when $p_{t}$ is lower, this indicates a sample is harder to classify, and it is given a higher weight.

SoftIoU loss [59] is a smoothed IoU-based metric designed to optimize the training process more effectively. Compared to traditional IoU loss, SoftIoU loss manages imbalances between classes better and updates the gradients more smoothly, thereby preventing oscillations during training.

$L_{s o f t i o u} = 1 - I o U = 1 - \frac{\sum_{i}^{N} P_{i} \cdot T_{i}}{\sum_{i}^{N} (P_{i} + T_{i} - P_{i} \cdot T_{i})}$

(7)

In this formula, N is the total number of pixels in an image, $P_{i}$ represents the probability predicted at the i-th pixel position, and $T_{i}$ denotes the ground-truth label at the i-th pixel position.

SoftIOU loss is used to stabilize the training process, while focal loss is used to mitigate the problem of class imbalances in samples. The final expression for the loss function is as follows:

$L o s s = F L + L_{S o f t I o U}$

(8)

4. Experiments

In this section, we will comprehensively introduce the details of the experiment, the dataset, the specifics about the experimental equipment and environment, the evaluation metrics, and the specifics of the design, along with outlining the visual and quantitative results of comparative experiments and the quantitative results of ablation studies.

4.1. The Dataset

Our experiments were conducted on the renowned IRSTD-1K dataset [20] and the MISTD dataset we built ourselves. IRSTD-1K consists of 1000 infrared images of real scenes, each with a resolution of 512 × 512 pixels, and all these images are annotated. This dataset features a variety of small targets, including drones and vehicles, within complex backgrounds, such as urban, rural, and river environments. Due to its inclusion of high-resolution, cluttered background noise and diverse types of targets, IRSTD-1K stands out as a benchmark dataset in the field of infrared small-target detection. The MISTD dataset we built ourselves includes 489 infrared images with a land background captured using the Qilu-1 satellite, and 1173 images with an urban background taken with an infrared mid-wave camera. To simulate small targets, we utilized Gaussian kernels. To introduce more randomness, we applied multiple Gaussian kernels that had undergone random elliptical scaling for random directional translations and concatenations. The peak and standard deviation of the Gaussian kernels were randomly generated. We integrate the NUDT-SIRST [18] public dataset into it, resulting in a hybrid dataset. In this study, we divided the above two datasets into training, validation, and test sets at a ratio of 5:3:2. Statistical information on the dataset is shown in Table 1.

4.2. Evaluation Metrics

P d

indicates the model’s ability to identify targets correctly, and it is defined as the ratio of the sum of correctly detected targets

T_{c o r r e c t}

to the sum of all targets

T_{a l l}

$P_{d} = \frac{T_{c o r r e c t}}{T_{a l l}}$

(9)

F a

indicates the model’s tendency to incorrectly classify negatives as positives, and it is defined as the ratio of false positive pixels

P_{f a l s e}

to the sum of all pixels

P_{a l l}

$F_{a} = \frac{P_{f a l s e}}{P_{a l l}}$

(10)

The ROC curve is a tool for evaluating the performance of binary classification models, with the probability of detection ( $P d$ ) and the false alarm rate ( $F a$ ) used as the y and x axes here. The curve being closer to the top-left corner represents a better model performance, and the area under the curve (AUC) indicates the overall performance of the model. The ROC curve is helpful for determining the optimal classification threshold and is widely applied in fields such as detection and segmentation.

The IoU (Intersection over the Union) is a commonly used metric for measuring the accuracy of the bounding boxes in object detection algorithms. It is defined as the ratio of the area of the intersection of two bounding boxes to the area of their union. In the field of image segmentation, the IoU is used to evaluate a model’s accuracy in classifying each pixel. By calculating the IoU between a model’s predicted segmentation result and the ground-truth labels, its segmentation accuracy can be quantified. In this paper, both the Intersection over the Union and the normalized Intersection over the Union [17] are used as evaluation metrics, both of which are pixel-level evaluation metrics.

The IoU is a metric used to measure the degree of overlap between two sets, typically between two regions (i.e., masks in this work). It is defined as follows:

$IoU = \frac{T P}{T + P - T P}$

(11)

where TP, T, and P denote the true positive pixels, true pixels, and positive pixels, respectively.

The nIoU was specifically tailored to the SIRST dataset to provide a more equitable metric that bridges the gap between model-driven and data-driven approaches. It is defined as follows:

$nIoU = \frac{1}{N} \sum_{i}^{N} \frac{T P [i]}{T [i] + P [i] - T P [i]}$

(12)

where N is the total number of targets.

Floating-point operations (FLOPs) and parameters (Params) are metrics used to assess the complexity of deep-learning models. FLOPs indicates the number of floating-point operations a model performs per second, while Params indicates the number of parameters the model needs to learn. These metrics help us to understand the computational demands and scale of a model, thereby aiding in model selection, optimization, and deployment. The magnitude of FLOPs reflects the complexity of a model; models with a higher number of FLOPs are more computationally complex. The number of Params reflects the size of a model, and smaller models involve lower computational burdens.

4.3. Implementation Details

We conducted sufficient experiments on the model proposed in this paper, including comparative experiments using the IRSTD-1k dataset and our own MISTD dataset, as well as ablation studies. The details of our training equipment are as follows: an NVIDIA RTX 2080 GPU (8 GB), 32 GB of RAM, an Intel Core i7-10700K CPU (3.8 GHz), the WSL operating system (Windows Subsystem for Linux), the deep-learning framework PyTorch 2.2, and Python 3.10. The experimental setup is as follows: images were uniformly resized to 256 × 256, the optimizer used was Adaptive Gradient (AdaGrad), the weight initialization method was Xavier initialization, the learning rate was set to 0.004, the number of training epochs was 500, the batch size was 8, and the loss functions used were focal and SoftIoU loss. Table 2 shows the details of the experimental configuration of the traditional methods in the comparative models.

4.4. Comparison with Various Methods

The quantitative results of the comparison given in Table 3 show that our method achieved the best performance on the IRSTD-1k and MISTD datasets while also achieving a balance between accuracy and the number of parameters. Traditional-model-based methods tend to perform poorly when dealing with complex backgrounds and datasets containing varying sizes and shapes, whereas data-driven deep-learning methods generally adapt well to the sizes of the targets and can effectively suppress background noise. Compared to other deep-learning approaches, our model has an advantage in capturing very small targets due to the combination of the powerful attention mechanism of the Mamba module and the capabilities of CNNs in local feature integration. Figure 3 shows an intuitive comparison of model performance.

To test whether the IoU values of our proposed method are superior to those of other high-performing methods, we designed significance tests for three other high-performing methods, as shown in Table 4. We applied the Student’s paired two-sample t-test, where each experiment fixed the same random seed to initialize different model parameters, retrained the models, and repeated the experiments 10 times to obtain 10 sets of IoU values. Subsequently, we conducted the Student’s t-test on these 10 sets of IoU values to examine whether the differences in IoU values were significant. The significance level was set at

α = 0.05

. The results of the significance tests indicate that our method outperforms the other methods in terms of IoU values, with p-values being less than 0.05. This demonstrates that the superiority of our method over the other comparison methods in terms of IoU values is significant.

A visual comparison of using our proposed method and other methods on the IRSTD-1k and MISTD datasets is presented in Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10. In these figures, we use red square boxes to frame detected targets, blue circles to frame missed targets, and yellow boxes to frame false detections. We also show a local amplification of the detection target. The traditional methods (RLCM, MPCM, and PSTNN) can detect brighter targets, but brighter noise from non-targets will also be detected, resulting in a higher false detection rate. For weak targets, the missed detection rate is too high. This is because the detection mechanism in the traditional methods is based on the difference in the intensity between the target and the background without considering information on the target’s shape and structure information; thus, the adaptability of this kind of scheme is poor. The scheme of the CNN is obviously superior to that of the traditional methods in dealing with the background. It adapts well to the background and provides good detection results in most scenarios. However, in the presence of complex backgrounds, missed detections and false detections still arise. The lightweight RDIAN model performs well in scenes with simple backgrounds but performs poorly where complex backgrounds and weak targets are concerned. Similar phenomena apply in several of the other models. In terms of retaining the shape features of targets, our method also exhibits a better performance than that of the other models, as well as better adaptability to complex backgrounds. As shown in the figures, our method yields good detection results in different scenarios. This is due to its combined ability to model the global context and capture local features, suppressing complex backgrounds, extracting targets from these complex backgrounds, and preserving the targets’ shape information well.

Table 5 shows the computational performance of the deep-learning-based models on the IRSTD-1k and MISTD datasets. It can be seen from the table that most of the models involve a large amount of calculation, making it difficult for them to meet the needs of real-time processing. The UIUnet model represents a particularly extreme example of this in that both its accuracy and number of parameters are high. The accuracy of the RDIAN lightweight model is lower than that of the other heavyweight models, but its real-time performance is very good. Our model achieves a good balance between the amount of calculation required and its accuracy, maintaining high accuracy and involving a lower amount of calculation.

4.5. The Ablation Study

To evaluate the contribution of each component to our model, we conducted a series of ablation studies. After systematically removing or modifying specific parts of the model, we then observed the resulting changes in its performance. This approach helped us understand the significance of each component and its impact on the model’s overall effectiveness.

4.5.1. The Ablation Study on the SSM Branch

To verify the contribution of the SSM branch to the detection accuracy, we conducted ablation experiments on the SSM branch separately using the two datasets IRSTD-1k and MISTD. The results in Table 6 show that removing the SSM module had a significant negative impact on the model’s accuracy, with its IoU and nIoU decreasing by

12.0 %

and

16.0 %

, respectively, for the IRSTD-1k dataset and Pd decreasing by

8.8 %

and Fa increasing by

10.74 \times 10^{- 5}

. For the MISTD dataset, its IoU and nIoU decreased by

9.1 %

and

6.8 %

, respectively; Pd decreased by

6.9 %

; and Fa increased by

5.37 \times 10^{- 5}

. These results demonstrate the SSM module’s ability to handle complex backgrounds and noise, as well as the effectiveness of its global attention mechanism in improving detection accuracy.

4.5.2. The Ablation Study on the CNN Branch

The CNN branch is divided into two modules, namely the FAB and the MSFB. We conducted ablation studies on these two modules to explore their impact on the model’s detection accuracy. The results in Table 6 show that when using the FAB module alone, the model’s IoU and nIoU on the IRSTD-1k dataset decreased by

6.7 %

and

9.1 %

, respectively; Pd decreased by

8.0 %

; and Fa increased by

13.54 \times 10^{- 5}

. When using the MSFB module alone, the model’s IoU and nIoU on the IRSTD-1k dataset decreased by

3.4 %

and

5.6 %

, respectively; Pd decreased by

7.2 %

; and Fa increased by

9.94 \times 10^{- 5}

. Similar trends were observed for the MISTD dataset. These results indicate that the capabilities of the FAB and MSFB modules in local feature extraction contribute to the model’s improvement in detection accuracy.

4.5.3. The Ablation Study on Loss Function

We conducted an ablation experiment to compare the selection of loss functions to verify the contribution of the loss function used in this method to the training effect. We selected two loss functions, Focal loss and SoftIoU loss, respectively, and obtained the comparison results on the data set, as shown in Table 7. As can be seen from the table, each evaluation indicator has a certain degree of loss. Therefore, we conclude that using two loss functions alone is not as good as using two loss functions at the same time for the final training results. This result verifies the contribution of the two loss functions, Focal loss and SoftIoU loss, to the training results. Their combination in use can achieve the best training accuracy.

Source link

Bolin Li www.mdpi.com

Greenberg News

A Hybrid Mamba–CNN UNet for Infrared Small Target Detection

1. Introduction

3. Methods

3.1. Preliminaries

3.1.1. The State Space Model

3.1.2. Discretization

3.2. Architecture

3.3. The HY-SSM Block

3.4. The Loss Function

4. Experiments

4.1. The Dataset

4.2. Evaluation Metrics

4.3. Implementation Details

4.4. Comparison with Various Methods

4.5. The Ablation Study

4.5.1. The Ablation Study on the SSM Branch

4.5.2. The Ablation Study on the CNN Branch

4.5.3. The Ablation Study on Loss Function

Greenberg

1. Introduction

3. Methods

3.1. Preliminaries

3.1.1. The State Space Model

3.1.2. Discretization

3.2. Architecture

3.3. The HY-SSM Block

3.4. The Loss Function

4. Experiments

4.1. The Dataset

4.2. Evaluation Metrics

4.3. Implementation Details

4.4. Comparison with Various Methods

4.5. The Ablation Study

4.5.1. The Ablation Study on the SSM Branch

4.5.2. The Ablation Study on the CNN Branch

4.5.3. The Ablation Study on Loss Function

Related Posts

China built out record amount of wind and solar power in 2024

Using Healthcare Redesign to Identify Medication Management Issues in Parkinson’s Disease

Trump wants Greenland. But what does Greenland want?

Greenberg