Greenberg News

    Green Futures: Innovate, Sustain, Thrive

    A Localized Scalable DNA Logic Circuit System Based on the DNA Origami Surface

    Greenberg     February 26, 2025 in News - 32 Minutes


    1. Introduction

    DNA (Deoxyribonucleic Acid) computing has an excellent ability to process information in parallel, benefiting from liquid-phase biomolecular interactions and the highly programmable nature of DNA molecules [1,2,3]. A seminal study in this field is that of Adleman, who solved the seven-city Hamilton path problem using DNA coding in 1994 [4]. DNA molecules have been used as computing substrates for computation and information processing and have evolved from the silicon-based computing paradigm to the parallel biocomputing paradigm. In DNA computing, DNA logic circuits are essential arithmetic architectures for digital computing, neural networks, molecular machines and algorithmic decision-making [5,6,7,8]. Concurrently, the excellent biocompatibility and nanoscale size of DNA molecules have facilitated the application of DNA logic circuits in the fields of biosensors, disease diagnosis and intelligent drug delivery [9,10,11,12]. Overall, DNA logic circuit systems have emerged as a quality interface for the cross-fusion of biotechnology and information technology.
    Over the past few decades, the strand displacement reaction (SDR) has been frequently employed as a reaction protocol to implement logical operations and information interactions in a DNA logic circuit system due to it being enzyme-free, programmable and high-efficiency [13,14,15,16,17,18]. In a DNA logic circuit system, single-stranded DNA is commonly used to represent the input of the binary digits 0/1, random collisions occur between DNA logic elements based on Brownian motion, the interactions between DNA molecules are triggered based on SDR protocol, and the logic outputs are read through signals such as fluorescence. However, the operation of discrete DNA logic systems in a solution is entirely dependent on the interactions between the discrete DNA logic components mediated by complex sequences. Such factors cause scalable discrete DNA logic circuit systems to suffer from slow dynamics and non-reusable sequences.
    To counter such issues, researchers have begun to introduce spatial constraints to construct fast and modular spatially localized DNA logic circuit systems. Several theoretical studies on the construction of spatially localized DNA circuit systems have been proposed [19,20,21]. With the development of DNA nanotechnology, particularly DNA origami, new design concepts for localized DNA circuit systems have been established [22,23,24,25,26,27]. DNA origami involves folding a long DNA scaffold strand into a two-dimensional rectangular platform. These DNA origami platforms provide an ideal surface for the construction of localized DNA logic systems, as the platforms are accompanied by uniformly distributed addressable sites and spatial constraints. In recent studies, several representative works have been proposed, such as a cargo sorting robot based on a two-dimensional DNA origami platform, single-molecule DNA navigators capable of performing maze searches, a spatially localized modular DNA circuit architecture based on the threshold strategy, a spatially localized DNA linear classifier for cancer diagnosis, and a strategy for high-speed sequential DNA computing using a solid-state DNA origami register [28,29,30,31,32].

    Despite these advances, constructing localized scalable DNA logic circuit systems remains a challenge. Here, we first constructed elementary two-input AND and OR logic circuits on a DNA origami surface, where logic operations were realized by triggering the SDR. We then showed that the constructed elementary logic circuits can be scaled up to form localized DNA logic circuit systems that perform arbitrary digital computing tasks, including square root functions, full adder and full subtractor. Lastly, we programmed and designed the elementary logic circuits and realized the application of the localized DNA logic circuit systems in three-satisfiability (3-SAT) problem solving and disease classification. In this work, we employed Visual DSD software (version “v2015-0325”) to simulate all the constructed DNA logic circuit systems, and the results showed that all the systems exhibit good stability and feasibility.

    2. Results

    2.1. Construction and Implementation of Elementary Logic Circuits and Cascades on the DNA Origami Surface

    In localized scalable DNA logic circuit systems, elementary logic circuits can be programmed and cascaded as the smallest logic units on the DNA origami surface to achieve the desired function (Figure 1a). One reported approach to designing elementary logic circuits on the DNA origami surface is the “threshold strategy”, which involves the use of a threshold DNA strand to compete with the output DNA strand to block signal propagation [29]. The toehold of the output DNA strand (3 nt (nucleotide)) was designed to be a truncated version of the threshold DNA strand (6 nt), which resulted in the signal preferentially binding to the threshold DNA strand until two signals were present. However, the “threshold strategy” requires four DNA strands to be anchored on the DNA origami surface to implement the elementary AND logic circuits (the anchoring efficiency of circuit components on the DNA origami surface impacts the performance of localized DNA logic circuit systems, Supplementary Text S1.1, Table S1 and Figure S1) and purposefully reduces the speed of signal propagation (the difference in signal propagation speed can cause the input strand to preferentially bind to the threshold hairpin strand, resulting in signal blocking). To more succinctly implement an elementary two-input AND logic circuit, we used only a DNA complex formed by base-pairing a hairpin DNA with a single strand of DNA (Figure 1b and Supplementary Figure S2). The DNA complex possessed two toeholds (A* and B*) that bind specifically to the input strands and that are confined to the origami surface by extending the poly 5T linker through staples within the DNA origami. When at most one input strand was added, the hairpin of the DNA complex could not be opened and could not react with the reporter molecule, resulting in a low output signal. When the two input strands were added, signal strand A first bound to toehold A*, and toehold B* was exposed with the SDR. Signal strand B bound to toehold B*, the hairpin of the DNA complex was turned on, and the exposed toehold R bound to the toehold R* of the reporter molecule, resulting in a high output signal (Supplementary Figure S3a). To implement an elementary two-input OR logic circuit, we used two simple hairpin DNA strands with two toeholds (A* and B*) that bind specifically to the input strands (Figure 1c). Once an input strand was added, the hairpin of the DNA strand was opened, and the exposed toehold R bound to the toehold R* of the reporter molecule, resulting in a high output signal (Supplementary Figure S3b).
    The elementary two-input AND logic circuit system based on the threshold strategy had seven circuit components, four of which were anchored on the DNA origami surface (Supplementary Figure S4a). The constructed elementary two-input AND logic circuit system had two components (a nearly 71% reduction of the circuit components, Supplementary Figure S4b,e), with only one component anchored to the DNA origami surface (nearly 75% reduction, Supplementary Figure S4f). Compared to the threshold strategy, the constructed elementary two-input OR logic circuit had a total of three components (a nearly 40% reduction, Supplementary Figure S4c–e), of which only two components are anchored to the DNA origami surface (a nearly 33% reduction, Supplementary Figure S4f).
    The cascadability of DNA logic circuits is a prerequisite for elementary logic circuits to be combined into large-scale DNA logic circuit systems. We first showed how two hairpin DNA strands cascade and interact on the DNA origami surface. As shown in Figure 2a, the fuel strand was designed to assist in the information interaction between the two hairpin DNA strands. When an input strand was added, it reacted with the first hairpin strand, and the exposed toehold R1 bound specifically to the toehold R1* of the fuel strand. The displaced single-strand DNA reacted with the second hairpin, and the exposed toehold R bound specifically to the toehold R* of the reporter molecule, resulting in a high output signal and completing the cascade interaction between the two hairpins. We demonstrated a localized OR–AND logic circuit system consisting of one elementary OR circuit, one AND circuit, one fuel strand and one reporter molecule (Figure 2b). For the localized OR–AND logic circuit system based on the threshold strategy, it was necessary to anchor roughly six circuit components on the DNA origami surface; in our work, however, it was only necessary to anchor three circuit components, reducing the required number of strands by nearly 50% (Supplementary Figure S5a,c,e). We tested all input combinations using Visual DSD software, with the outputs moving to the correct signals. The simulation results showed that all the reactions were completed in a short time span, and the constructed elementary logic circuits can effectively cascade and interact.

    2.2. Scaling up the Localized DNA Logic Circuit Systems for Digital Computing

    To exemplify that scaling up elementary DNA logic circuits can realize arbitrary digital computation tasks, we demonstrated a circuit system that computes the floor of the square root of a four-bit binary number, a full adder circuit system and a full subtractor system. DNA logic circuit systems may produce a false output before all inputs have been added, as a result of the NOT gate having already generated a signal without inputs. Therefore, dual-rail logic is necessary in scalable DNA logic circuit systems. Dual-rail logic refers to the fact that each input X in a logic gate is replaced by a pair of inputs, X1 and X0, representing the binary numbers “1” and “0”, respectively. The layout of the localized circuit system for computing the floor of the square root of a four-bit binary number on the DNA origami surface is shown in Figure 2c. The entire circuit system had two layers, including the cascade of two OR circuits and two AND circuits, one fuel strand and two reporter molecules. For the circuit system based on the threshold strategy to compute the floor of the square root of a four-bit binary number, it was necessary to anchor roughly 12 circuit components on the DNA origami surface; in our work, however, it was only necessary to anchor 6 components, reducing the number of required strands by nearly 50% (Supplementary Figure S5b,d,f). We tested all 16 possible four-bit inputs from 0000 to 1111 using Visual DSD software, and all the outputs moved to the correct signals (Supplementary Figure S6). Four representative examples are shown in the right column of Figure 2c.
    We further scaled up the circuit systems to implement the addition and subtraction of binary numbers. A full adder is a circuit system that implements binary addition operations with an additional Carry input, Cin, as the third input, producing two outputs, a sum (S) and a Carry (Cout). The layout of the DNA full adder circuit system on the DNA origami surface is shown in Figure 3a. The entire full adder circuit system had two layers, including nine AND circuits, three fuel strands and two reporter molecules. We tested all input combinations using Visual DSD software, and all the outputs went to the correct signals (Figure 3b). A full subtractor is a circuit system that implements the binary subtraction operations with a borrowed input from the lower bit, Bin, as the third input, producing two outputs, a difference (Di) and a borrowed output to the higher bit (Bout). The layout of the DNA full subtractor circuit system on the DNA origami surface is shown in Figure 4a. The entire full subtractor circuit system had two layers, including seven AND circuits, two fuel strands and four reporter molecules. We tested all input combinations using Visual DSD software, and all the outputs moved to the correct signals (Figure 4b).
    Notably, we attempted to place the full adder and full subtractor circuit systems on the same DNA origami surface (Supplementary Figure S7a). The placement of the full adder and full subtractor on the same DNA origami surface can realize parallel computation because of the high parallelism of the biochemical reaction; put simply, the same set of binary numbers can be added and subtracted simultaneously (Figure 4c and Supplementary Figure S7b,c). Here, DNA origami can be similarly viewed as a liquid-phase biochip, and the DNA strands anchored to the DNA origami surface are analogous to circuit components on a semiconductor chip. Unlike semiconductor chips, DNA-based biochips have high parallelism, and this change from the underlying computing mode provides DNA computing with strong computing power.

    2.3. Integrated Localized DNA Logic Circuit Systems for Solving the 3-SAT Problem

    To further demonstrate the power of the constructed DNA circuits in solving complex NP (Non-deterministic Polynomial)-complete problems, we used the constructed elementary logic circuits to integrate a DNA logic circuit system for solving the 3-SAT problem with four variables (Figure 5a and Supplementary Text S1.2). The layout of the integrated DNA logic circuit system on the DNA origami surface is shown in Figure 5a. The integrated circuit system was more complex than the circuit systems of square root, full adder and full subtractor, and the entire circuit system had four layers, including 8 OR circuits, 3 AND circuits, 10 fuel strands and 1 reporter molecule. We tested all 16 possible input combinations, and the integrated DNA logic circuit system was able to accurately acquire 10 solutions to the 3-SAT problem from the data pool of 16 possible solutions (Figure 5b).
    Considering that 19 localized circuit components were required to solve the 3-SAT problem with 4 clauses and that there are nearly 100 addressable sites on the DNA origami surface, we estimated that up to 60 (20 clauses, 60 variables) variables of the 3-SAT problems were allowed to be solved (Supplementary Figure S8), making it possible to solve the larger scale 3-SAT problem with the integrated DNA circuit system.

    2.4. Localized DNA Logic Circuit Systems for Disease Classification

    DNA logic circuit systems have excellent analysis and decision-making capabilities. We scaled up the constructed elementary logic circuits into a localized DNA logic circuit system for germ cell tumor (GCT) state classification (healthy or diseased). A strong correlation exists between microRNA (miRNA) expression levels and cancer. We used the miRNA expression data of GCT samples from The Cancer Genome Atlas (TCGA) and the random forest algorithm to train the model (263 GCT and 23 healthy samples), and screened out the characteristic miRNAs (miRNA-345, miRNA-17, miRNA-139, miRNA-210, miRNA-7705 and miRNA-1-1) associated with GCT (Figure 6a). We used a localized
    DNA logic circuit system containing 1 OR circuit, 10 AND circuits, 4 fuel strands and 2 reporter molecules to map the decision tree of miRNAs (Figure 6b,c), and then classified the state of GCT samples based on the miRNA expression levels. The miRNA expression level below the threshold was set as the logical signal X0, and above the threshold was set as the logical signal X1. We used 25 randomized miRNA expression samples from GCT samples from TCGA to test the constructed localized DNA logic circuit system for performing disease classification. Visual DSD software was used to test the analysis and classification of each dataset. The results showed agreement between the actual disease states labeled in TCGA, the random forest model and the constructed localized DNA logic circuit system (Figure 6d,e and Supplementary Figure S9).

    3. Discussion

    Herein, we demonstrated a strategy for constructing localized scalable DNA logic circuit systems based on the DNA origami surface. We first constructed elementary two-input AND and OR logic circuits on the DNA origami surface using only one and two circuit components, respectively. We then showed that the constructed elementary logic circuits can be scaled up to an arbitrary localized circuit system to implement functions such as square root circuit, full adder and full subtractor. The constructed localized scalable DNA logic circuit system based on the DNA origami surface has several advantages as follows: (1) The first is scalability, whereby the elementary two-input AND and OR logic circuits can be scaled up into large-scale localized DNA logic circuit systems. In addition, compared with the threshold strategy, our strategy involved the use of fewer circuit components on the DNA origami surface, which effectively avoids signal attenuation caused by having many components. (2) The second is modularity, which allows circuit components to be embedded anywhere in the system, and different logic functions are realized through reasonable cascading design. (3) The third is strong functionality; the constructed localized DNA logic circuit system can be effectively applied to digital computing and disease diagnosis (such as solving 3-SAT problems and classification of disease states).

    We believe that the programmability and scalability of the constructed localized DNA logic circuit systems can be extended in the fields of digital computation, disease diagnosis and NP-complete problem solving. However, there are challenges that need to be addressed as the size of the problem or the amount of data associated with the disease increases. Such challenges include the following: (1) Further scaling of the size of the localized DNA logic circuit systems is constrained by the size of the DNA origami, and DNA origami of a larger size is required. (2) When performing disease diagnosis, the logic circuit system can only passively receive the 0/1 signal (for example, the miRNA expression level is set to 1 above the threshold concentration and 0 below the threshold concentration) and realize a classification decision, and logic circuit system cannot directly read the miRNA expression level above/below the threshold concentration from the samples, which impacts the efficiency and integration of disease diagnosis. Introducing a DNA chemical reaction network that can directly read the expression level of miRNA represents a potential future direction.

    4. Materials and Methods

    4.1. Simulation Experiments Based on Visual DSD Software

    Visual DSD is a programming language and software tool for simulating DNA computing systems based on SDR. It was originally proposed by Andrew Phillips and coworkers in 2009 and has been extended with modeling, embedding biochemical experimental data and analysis capabilities [33,34,35,36,37,38,39]. Visual DSD can automatically demonstrate all possible displacement reactions between all kinds of DNA without the need to manually construct a reaction network. Visual DSD has become a powerful tool for visualizing and simulating DNA computing systems based on SDR. The Visual DSD software version used in this paper is ‘v2015-0325’. The user manual for the Visual DSD software is available online at “UPL: https://www.microsoft.com/en-us/research/uploads/prod/2009/02/Visual_DSD_Manual.pdf (accessed on 1 February 2025).
    To analyze the process of SDR and predict the performance of the DNA circuits, the parameters in the Visual DSD simulation programs were set as shown in Table 1, which are able to simulate all the possible reactions between the DNA molecules.

    4.2. Silicon-Based Training of Germ Cell Tumor (GCT) Data

    We used the miRNA expression data of GCT samples from The Cancer Genome Atlas (TCGA) and the random forest algorithm to train the model (263 GCT and 23 healthy samples), with 60% of samples used for training and 40% of samples used for testing. Random forests achieve classification or regression by integrating multiple decision trees based on different sample subsets and feature subsets, and the classification results are determined by majority voting:

    y ∧ = arg max c ∑ t = 1 T ∐ ( h t ( X ) = c )

    or by the mean of the regression tree:

    y ∧ = 1 T ∑ t = 1 T h t ( X )

    The experimental environment was Windows 10 operating system and Intel Core i5. We screened out the characteristic miRNAs (miRNA-345, miRNA-17, miRNA-139, miRNA-210, miRNA-7705 and miRNA-1-1) associated with GCT, achieving 94% accuracy in GCT identification.

    5. Conclusions

    DNA origami provides a nanoscale addressable surface for the construction of DNA logic circuit systems. These localized DNA logic circuit systems constrained on the DNA origami surface have faster reaction dynamics than discrete DNA logic circuit systems. Therefore, in this paper, we proposed a strategy for constructing localized scalable DNA logic circuit systems based on a DNA origami surface and further implemented complex logic circuit systems such as square root circuit, full adder, full subtractor and logic circuit systems for solving 3-SAT problems and disease classification. This strategy involved the use of fewer circuit components on the DNA origami surface to achieve the construction of DNA logic circuit systems. We verified the feasibility, scalability and stability of the constructed localized DNA logic circuit systems through simulation experiments based on Visual DSD software. This work is expected to provide a solid foundation for intelligent integrated DNA computing systems.

    Supplementary Materials

    Author Contributions

    Conceptualization, Z.T. and Z.Y.; methodology, Z.T.; software, Z.T., S.L. and C.C.; validation, Z.T., Z.Z. and Z.Y.; formal analysis, S.L.; investigation, Z.T.; resources, Z.Y.; data curation, Z.Y.; writing—original draft preparation, Z.T.; writing—review and editing, Z.Y.; visualization, S.L., C.C. and Z.Z.; supervision, Z.T.; project administration, Z.Y.; funding acquisition, Z.T. and Z.Y. All authors have read and agreed to the published version of the manuscript.

    Funding

    This research was funded by the National Natural Science Foundation of China (grant numbers: 22307072 and 62272005) and sponsored by the Chenguang Program supported by the Shanghai Education Development Foundation and Shanghai Municipal Education Commission.

    Institutional Review Board Statement

    Not applicable.

    Informed Consent Statement

    Not applicable.

    Data Availability Statement

    Conflicts of Interest

    The authors declare no conflicts of interest.

    Abbreviations

    The following abbreviations are used in this manuscript:

    SDRStrand Displacement Reaction
    3-SATThree-Satisfiability
    miRNAMicroRNA
    GCTGerm Cell Tumor
    TCGAThe Cancer Genome Atlas
    NPNon-deterministic Polynomial
    DNADeoxyribonucleic Acid
    ntnucleotide

    References

    1. Seelig, G.; Soloveichik, D.; Zhang, D.Y.; Winfree, E. Enzyme-free nucleic acid logic circuits. Science 2006, 314, 1585–1588. [Google Scholar] [CrossRef] [PubMed]
    2. Qian, L.L.; Winfree, E. Scaling up digital circuit computation with DNA strand displacement cascades. Science 2011, 332, 1196–1201. [Google Scholar] [CrossRef] [PubMed]
    3. Lv, H.; Xie, N.L.; Li, M.Q.; Dong, M.K.; Sun, C.Y.; Zhang, Q.; Zhao, L.; Li, J.; Zuo, X.L.; Chen, H.B.; et al. DNA-based programmable gate arrays for general-purpose DNA computing. Nature 2023, 622, 292–300. [Google Scholar] [CrossRef]
    4. Adleman, L.M. Molecular computation of solutions to combinatorial problems. Science 1994, 266, 1021–1024. [Google Scholar] [CrossRef] [PubMed]
    5. Santini, C.C.; Bath, J.; Turberfield, A.J.; Tyrrell, A.M. A DNA network as an information processing system. Int. J. Mol. Sci. 2012, 13, 5125–5137. [Google Scholar] [CrossRef] [PubMed]
    6. Cherry, K.M.; Qian, L.L. Scaling up molecular pattern recognition with DNA-based winner-take-all neural networks. Nature 2018, 559, 370–376. [Google Scholar] [CrossRef]
    7. Wang, J.; Zhang, X.K.; Shi, P.J.; Cao, B.; Wang, B. A DNA finite-state machine based on the programmable allosteric strategy of DNAzyme. Int. J. Mol. Sci. 2023, 24, 3588. [Google Scholar] [CrossRef]
    8. Xiong, X.W.; Zhu, T.; Zhu, Y.; Cao, M.Y.; Xiao, J.; Li, L.; Wang, F.; Fan, C.H.; Pei, H. Molecular convolutional neural networks with DNA regulatory circuits. Nat. Mach. Intell. 2022, 4, 625–635. [Google Scholar] [CrossRef]
    9. Wang, Z.C.; Pu, J.; Cao, L.L.; Tian, J. A parallel biological optimization algorithm to solve the unbalanced assignment problem based on DNA molecular computing. Int. J. Mol. Sci. 2015, 16, 25338–25352. [Google Scholar] [CrossRef] [PubMed]
    10. Zhang, C.; Zheng, T.T.; Ma, Q.; Yang, L.L.; Zhang, M.Z.; Wang, J.Y.; Teng, X.Y.; Miao, Y.Y.; Lin, H.C.; Yang, Y.; et al. Logical analysis of multiple single-nucleotide-polymorphisms with programmable DNA molecular computation for clinical diagnostics. Angew Chem. Int. Ed. Engl. 2022, 4, e202117658. [Google Scholar] [CrossRef] [PubMed]
    11. Yin, F.F.; Zhao, H.P.; Lu, S.S.; Shen, J.W.; Li, M.; Mao, X.H.; Li, F.; Shi, J.Y.; Li, J.; Dong, B.J.; et al. DNA-framework-based multidimensional molecular classifiers for cancer diagnosis. Nat. Nanotechnol. 2023, 18, 677–686. [Google Scholar] [CrossRef]
    12. Yin, J.; Wang, S.Y.; Wang, J.H.; Zhang, Y.W.; Fan, C.H.; Chao, J.; Gao, Y.; Wang, L.H. An intelligent DNA nanodevice for precision thrombolysis. Nat. Mater. 2024, 23, 854–862. [Google Scholar] [CrossRef] [PubMed]
    13. Benenson, Y.; Paz-Elizur, T.; Adar, R.; Keinan, E.; Livneh, Z.; Shapiro, E. Programmable and autonomous computing machine made of biomolecules. Nature 2001, 414, 430–434. [Google Scholar] [CrossRef] [PubMed]
    14. Wang, F.; Lv, H.; Li, Q.; Li, J.; Zhang, X.L.; Shi, J.Y.; Wang, L.H.; Fan, C.H. Implementing digital computing with DNA-based switching circuits. Nat. Commun. 2020, 11, 121. [Google Scholar] [CrossRef]
    15. Liu, C.J.; Liu, Y.; Zhu, E.Q.; Zhang, Q.; Wei, X.P.; Wang, B. Cross-Inhibitor: A time-sensitive molecular circuit based on DNA strand displacement. Nucleic Acids Res. 2020, 48, 10691–10701. [Google Scholar] [CrossRef] [PubMed]
    16. Lapteva, A.P.; Sarraf, N.; Qian, L.L. DNA strand-displacement temporal logic circuits. J. Am. Chem. Soc. 2022, 144, 12443–12449. [Google Scholar] [CrossRef] [PubMed]
    17. Xie, N.L.; Li, M.Q.; Wang, Y.; Lv, H.; Shi, J.Y.; Li, J.; Li, Q.; Wang, F.; Fan, C.H. Scaling up multi-bit DNA full adder circuits with minimal strand displacement reactions. J. Am. Chem. Soc. 2022, 144, 9479–9488. [Google Scholar] [CrossRef] [PubMed]
    18. Bucci, J.; Irmisch, P.; Grosso, E.D.; Seidel, R.; Ricci, F. Timed pulses in DNA strand displacement reactions. J. Am. Chem. Soc. 2023, 145, 20968–20974. [Google Scholar] [CrossRef] [PubMed]
    19. Teichmann, M.; Kopperger, E.; Simmel, F.C. Robustness of localized DNA strand displacement cascades. ACS Nano 2014, 8, 8487–8496. [Google Scholar] [CrossRef]
    20. Dalchau, N.; Chandran, H.; Gopalkrishnan, N.; Phillips, A.; Reif, J. Probabilistic analysis of localized DNA hybridization circuits. ACS Synth. Biol. 2015, 4, 898–913. [Google Scholar] [CrossRef]
    21. Ruiz, I.M.; Arbona, J.M.; Lad, A.; Mendoza; Aiméa, J.P.; Elezgaray, J. Connecting localized DNA strand displacement reactions. Nanoscale 2015, 7, 12970–12978. [Google Scholar] [CrossRef]
    22. Seeman, N.C. Nucleic acid junctions and lattices. J. Theor. Biol. 1982, 99, 37–47. [Google Scholar] [CrossRef]
    23. Bui, H.; Shah, S.; Mokhtar, R.; Song, T.Q.; Garg, S.; Reif, J. Localized DNA hybridization chain reactions on DNA origami. ACS Nano 2018, 12, 1146–1155. [Google Scholar] [CrossRef]
    24. Petersen, P.; Tikhomirov, G.; Qian, L.L. Information-based autonomous reconfiguration in systems of interacting DNA nanostructures. Nat. Commun. 2018, 9, 5362. [Google Scholar] [CrossRef]
    25. Liu, L.; Hong, F.; Liu, H.; Zhou, X.; Jiang, S.X.; Sulc, P.; Jiang, J.H.; Yan, H. A localized DNA finite-state machine with temporal resolution. Sci. Adv. 2022, 8, eabm9530. [Google Scholar] [CrossRef] [PubMed]
    26. Sarraf, N.; Rodriguez, K.R.; Qian, L.L. Modular reconfiguration of DNA origami assemblies using tile displacement. Sci. Robot. 2023, 8, eadf1511. [Google Scholar] [CrossRef] [PubMed]
    27. Tikhomirov, G.; Petersen, P.; Qian, L.L. Fractal assembly of micrometre-scale DNA origami arrays with arbitrary patterns. Nature 2017, 552, 67–71. [Google Scholar] [CrossRef] [PubMed]
    28. Thubagere, A.J.; Li, W.; Johnson, R.F.; Chen, Z.; Doroudi, S.; Lee, Y.; Izatt, G.; Wittman, S.; Srinivas, N.; Woods, D.; et al. A cargo-sorting DNA robot. Science 2017, 357, eaan6558. [Google Scholar] [CrossRef] [PubMed]
    29. Chatterjee, G.; Dalchau, N.; Muscat, R.A.; Phillips, A.; Seelig, G. A spatially localized architecture for fast and modular DNA computing. Nat. Nanotechnol. 2017, 12, 920–927. [Google Scholar] [CrossRef] [PubMed]
    30. Chao, J.; Wang, J.; Wang, F.; Ouyang, X.Y.; Kopperger, E.; Liu, H.J.; Li, Q.; Shi, J.Y.; Wang, L.H.; Hu, J.; et al. Solving mazes with single-molecule DNA navigators. Nat. Mater. 2019, 18, 273–279. [Google Scholar] [CrossRef] [PubMed]
    31. Yang, L.L.; Tang, Q.; Zhang, M.Z.; Tian, Y.; Chen, X.X.; Xu, R.; Ma, Q.; Guo, P.; Zhang, C.; Han, D. A spatially localized DNA linear classifier for cancer diagnosis. Nat. Commun. 2024, 15, 4583. [Google Scholar] [CrossRef] [PubMed]
    32. Zhang, Q.; Li, M.Q.; Tang, Y.Q.; Zhang, J.Y.; Sun, C.Y.; Hao, Y.Y.; Cheng, J.N.; Xie, X.D.; Jia, S.S.; Lv, H.; et al. High-speed sequential DNA computing using a solid-state DNA origami register. ACS Cent. Sci. 2024, 10, 2285–2293. [Google Scholar] [CrossRef] [PubMed]
    33. Phillips, A.; Cardelli, L. A programming language for composable DNA circuits. J. R. Soc. Interface 2009, 6, S419–S436. [Google Scholar] [CrossRef]
    34. Lakin, M.R.; Youssef, S.; Polo, F.; Emmott, S.; Phillips, A. Visual DSD: A design and analysis tool for DNA strand displacement systems. Bioinformatics 2011, 27, 3211–3213. [Google Scholar] [CrossRef] [PubMed]
    35. Lakin, M.R.; Paulevé, L.; Phillips, A. Stochastic simulation of multiple process calculi for biology. Theor. Comput. Sci. 2012, 431, 181–206. [Google Scholar] [CrossRef]
    36. Chen, Y.; Dalchau, N.; Srinivas, N.; Phillips, A.; Cardelli, L.; Soloveichik, D.; Seelig, G. Programmable chemical controllers made from DNA. Nat. Nanotechnol. 2013, 8, 755–762. [Google Scholar] [CrossRef]
    37. Yordanov, B.; Kim, J.; Petersen, R.L.; Shudy, A.; Kulkarni, V.V.; Phillips, A. Computational design of nucleic acid feedback control circuits. ACS Synth. Biol. 2014, 3, 600–616. [Google Scholar] [CrossRef]
    38. Spaccasassi, C.; Lakin, M.R.; Phillips, A. A logic programming language for computational nucleic acid devices. ACS Synth. Biol. 2019, 8, 1530–1547. [Google Scholar] [CrossRef] [PubMed]
    39. Lakin, M.R.; Youssef, S.; Cardelli, L.; Phillips, A. Abstractions for DNA circuit design. J. R. Soc. Interface 2012, 9, 470–486. [Google Scholar] [CrossRef]
    40. Jungmann, R.; Avendaño, M.S.; Dai, M.; Woehrstein, J.B.; Agasti, S.S.; Feiger, Z.; Rodal, A.; Yin, P. Quantitative super-resolution imaging with qPAINT. Nat. Methods 2016, 13, 439–442. [Google Scholar] [CrossRef] [PubMed]
    41. Strauss, M.T.; Schueder, F.; Haas, D.; Nickels, C.P.; Jungmann, R. Quantifying absolute addressability in DNA origami with molecular resolution. Nat. Commun. 2018, 9, 1600. [Google Scholar] [CrossRef] [PubMed]
    42. Lipton, R.J. DNA solution of hard computational problems. Science 1995, 268, 542–545. [Google Scholar] [CrossRef]
    43. Braich, R.S.; Chelyapov, N.; Johnson, C.; Rothemund, P.W.K.; Adleman, L. Solution of a 20-variable 3-SAT problem on a DNA computer. Science 2002, 296, 499–502. [Google Scholar] [CrossRef] [PubMed]
    44. Rothemund, P.W.K. Folding DNA to create nanoscale shapes and patterns. Nature 2006, 440, 297–302. [Google Scholar] [CrossRef] [PubMed]
    Figure 1.
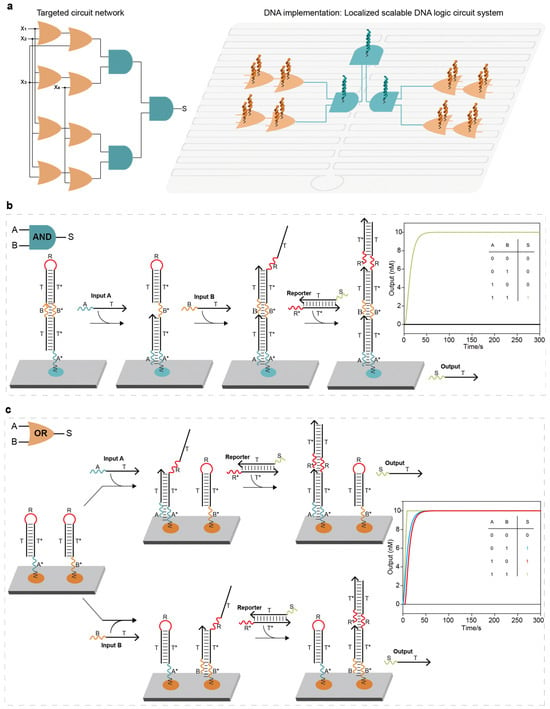
    Construction of the localized elementary DNA logic circuit: (a) An abstraction of a localized DNA logic circuit system. Scaling up elementary logic circuits into localized DNA logic circuit systems through deliberate programming allows for the realization of a targeted circuit network. (b) Elementary two-input AND logic circuit. The entire system consisted of a localized DNA complex (with two toeholds A* and B*) and a reporter molecule. The base sequences of domain and domain* of the same letter were completely complementary. When two signal strands were added, the hairpin of the DNA complex was opened and reacted with the reporter molecule, displacing the output strand and producing a high signal. (c) Elementary two-input OR logic circuit. The entire system consisted of two localized hairpin DNA strands with two toeholds (A* and B*) and a reporter molecule. Once an input strand was added, the hairpin of the DNA strand was opened and reacted with the reporter molecule, displacing the output strand and producing a high signal. The colorful lines corresponded to reaction kinetics curves with the same color numbers.

    Figure 1.
    Construction of the localized elementary DNA logic circuit: (a) An abstraction of a localized DNA logic circuit system. Scaling up elementary logic circuits into localized DNA logic circuit systems through deliberate programming allows for the realization of a targeted circuit network. (b) Elementary two-input AND logic circuit. The entire system consisted of a localized DNA complex (with two toeholds A* and B*) and a reporter molecule. The base sequences of domain and domain* of the same letter were completely complementary. When two signal strands were added, the hairpin of the DNA complex was opened and reacted with the reporter molecule, displacing the output strand and producing a high signal. (c) Elementary two-input OR logic circuit. The entire system consisted of two localized hairpin DNA strands with two toeholds (A* and B*) and a reporter molecule. Once an input strand was added, the hairpin of the DNA strand was opened and reacted with the reporter molecule, displacing the output strand and producing a high signal. The colorful lines corresponded to reaction kinetics curves with the same color numbers.

    Figure 2.
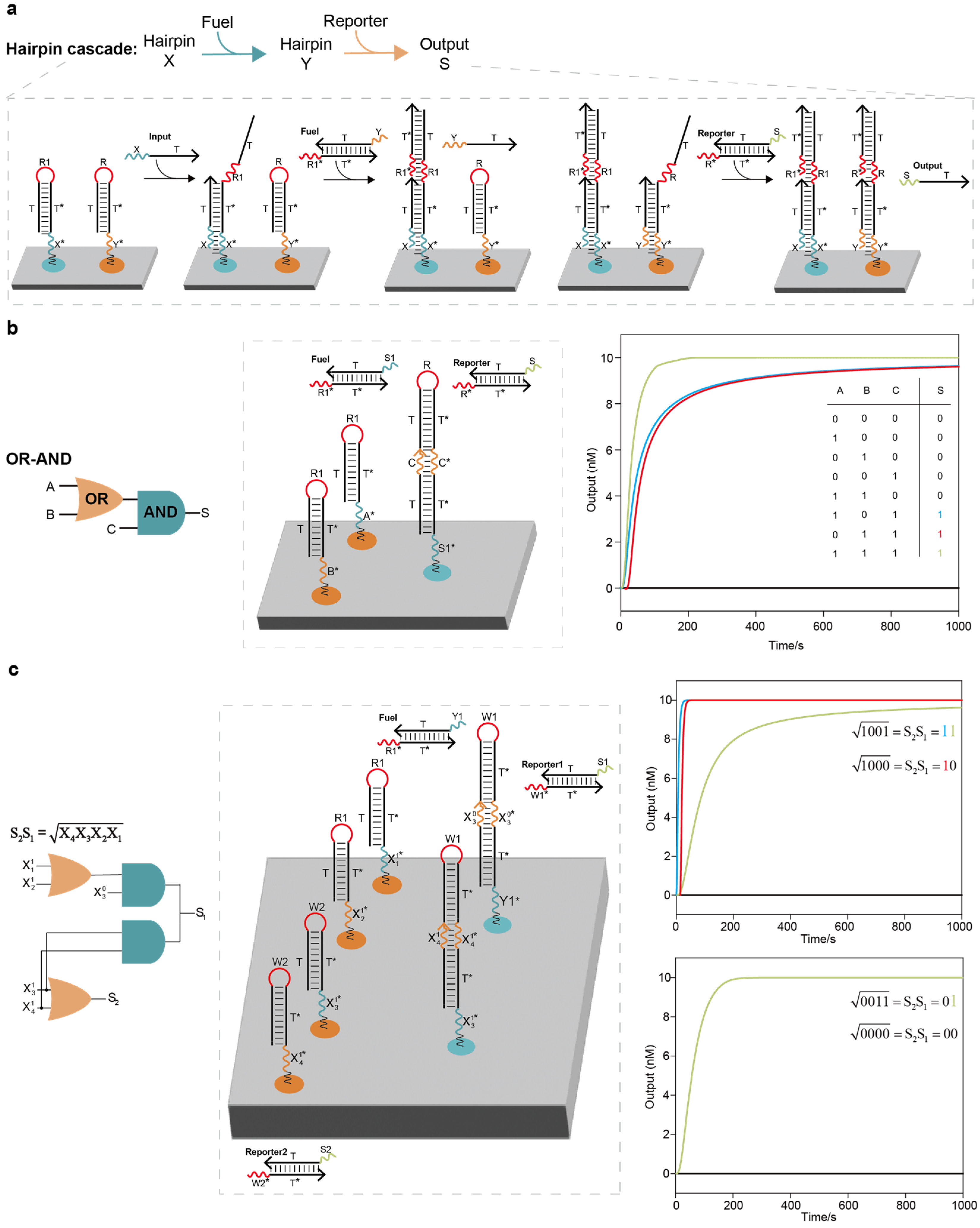
    Implementation of the localized elementary DNA logic circuit cascade and localized DNA logic circuit system for computing the floor of the square root of a four-bit binary number: (a) Hairpin cascade. The two hairpin DNA strands were cascaded with the assistance of the fuel strand. (b) OR–AND circuit cascade. The entire system consisted of 1 elementary OR circuit, 1 AND circuit, 1 fuel strand and 1 reporter molecule. For the localized OR–AND logic circuit system based on the threshold strategy, it was necessary to anchor roughly 6 circuit components on the DNA origami surface; in our work, however, it was only necessary to anchor 3 circuit components, reducing the required number of strands by nearly 50%. (c) Localized DNA logic circuit system for computing the floor of the square root of a four-bit binary number. The entire circuit system had two layers, including the cascade of 2 OR circuits and 2 AND circuits, 1 fuel strand and 2 reporter molecules. For the circuit system based on the threshold strategy to compute the floor of the square root of a four-bit binary number, it was necessary to anchor roughly 12 circuit components on the DNA origami surface; in our work, however, it was only necessary to anchor 6 components, reducing the required number of strands by nearly 50%. Four representative examples are shown in the right column.

    Figure 2.
    Implementation of the localized elementary DNA logic circuit cascade and localized DNA logic circuit system for computing the floor of the square root of a four-bit binary number: (a) Hairpin cascade. The two hairpin DNA strands were cascaded with the assistance of the fuel strand. (b) OR–AND circuit cascade. The entire system consisted of 1 elementary OR circuit, 1 AND circuit, 1 fuel strand and 1 reporter molecule. For the localized OR–AND logic circuit system based on the threshold strategy, it was necessary to anchor roughly 6 circuit components on the DNA origami surface; in our work, however, it was only necessary to anchor 3 circuit components, reducing the required number of strands by nearly 50%. (c) Localized DNA logic circuit system for computing the floor of the square root of a four-bit binary number. The entire circuit system had two layers, including the cascade of 2 OR circuits and 2 AND circuits, 1 fuel strand and 2 reporter molecules. For the circuit system based on the threshold strategy to compute the floor of the square root of a four-bit binary number, it was necessary to anchor roughly 12 circuit components on the DNA origami surface; in our work, however, it was only necessary to anchor 6 components, reducing the required number of strands by nearly 50%. Four representative examples are shown in the right column.

    Ijms 26 02043 g002
    Figure 3.
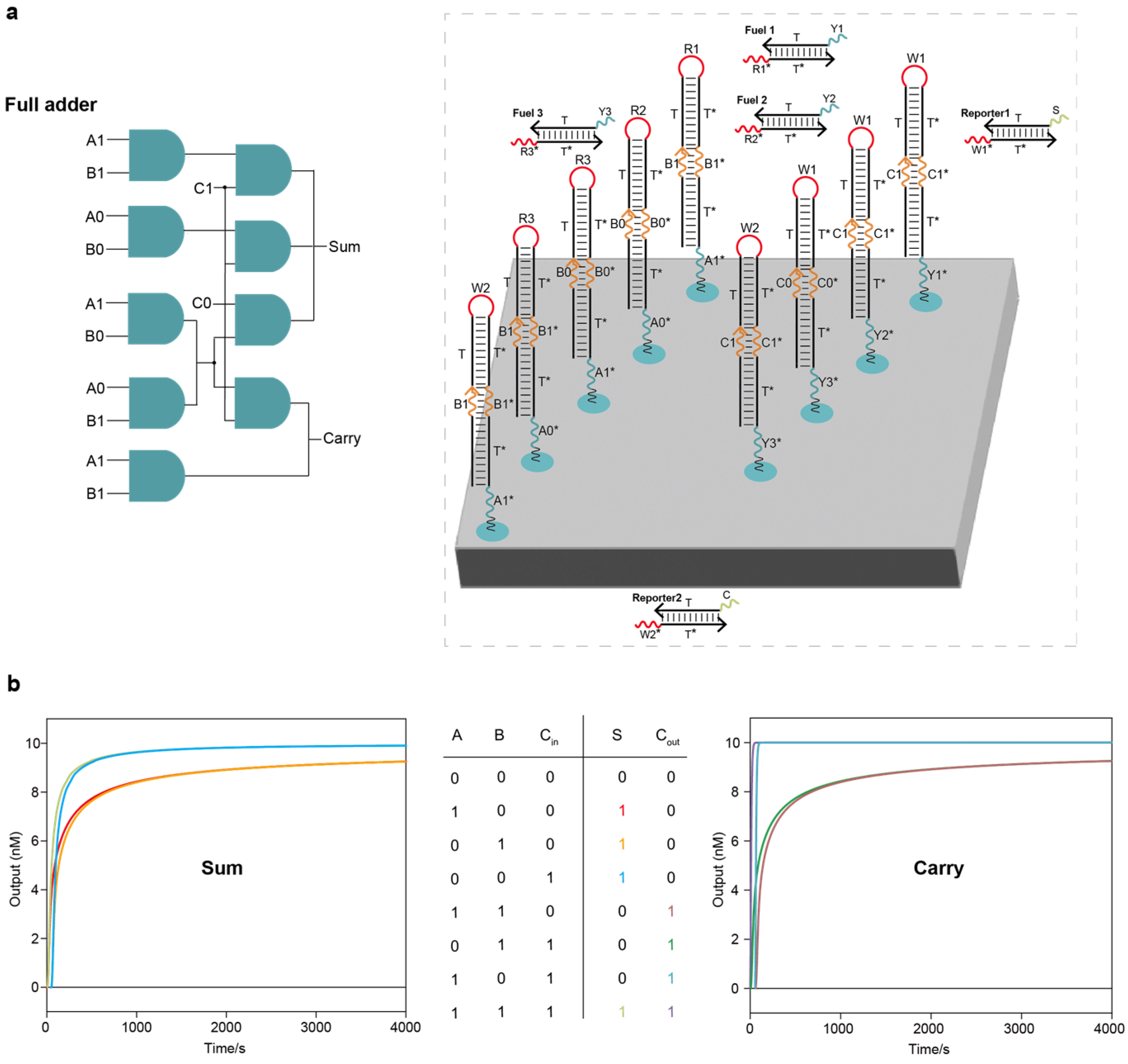
    Localized DNA full adder circuit system: (a) The layout of the DNA full adder circuit system on the DNA origami surface. The entire full adder circuit system had two layers, including 9 AND circuits, 3 fuel strands and 2 reporter molecules. (b) Test results under all input combinations using Visual DSD software.

    Figure 3.
    Localized DNA full adder circuit system: (a) The layout of the DNA full adder circuit system on the DNA origami surface. The entire full adder circuit system had two layers, including 9 AND circuits, 3 fuel strands and 2 reporter molecules. (b) Test results under all input combinations using Visual DSD software.

    Ijms 26 02043 g003
    Figure 4.
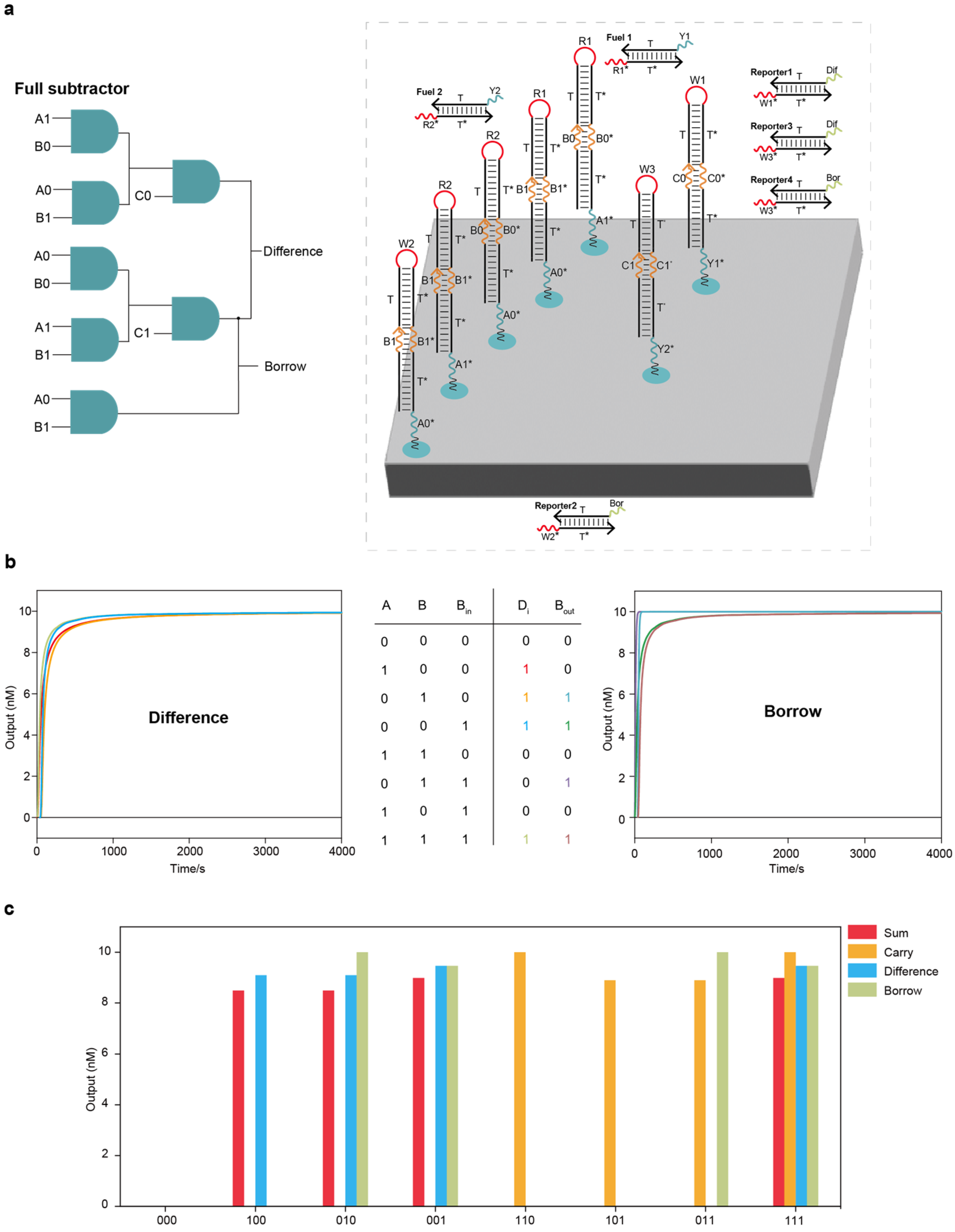
    Localized DNA full subtractor circuit system and parallel computing of full adder and full subtractor circuit systems: (a) The layout of the DNA full subtractor circuit system on the DNA origami surface. The entire full subtractor circuit system had two layers, including 7 AND circuits, 2 fuel strands and 4 reporter molecules. (b) Test results under all input combinations using Visual DSD software. (c) Test results of parallel computing of full adder and full subtractor circuit systems using Visual DSD software.

    Figure 4.
    Localized DNA full subtractor circuit system and parallel computing of full adder and full subtractor circuit systems: (a) The layout of the DNA full subtractor circuit system on the DNA origami surface. The entire full subtractor circuit system had two layers, including 7 AND circuits, 2 fuel strands and 4 reporter molecules. (b) Test results under all input combinations using Visual DSD software. (c) Test results of parallel computing of full adder and full subtractor circuit systems using Visual DSD software.

    Ijms 26 02043 g004
    Figure 5.
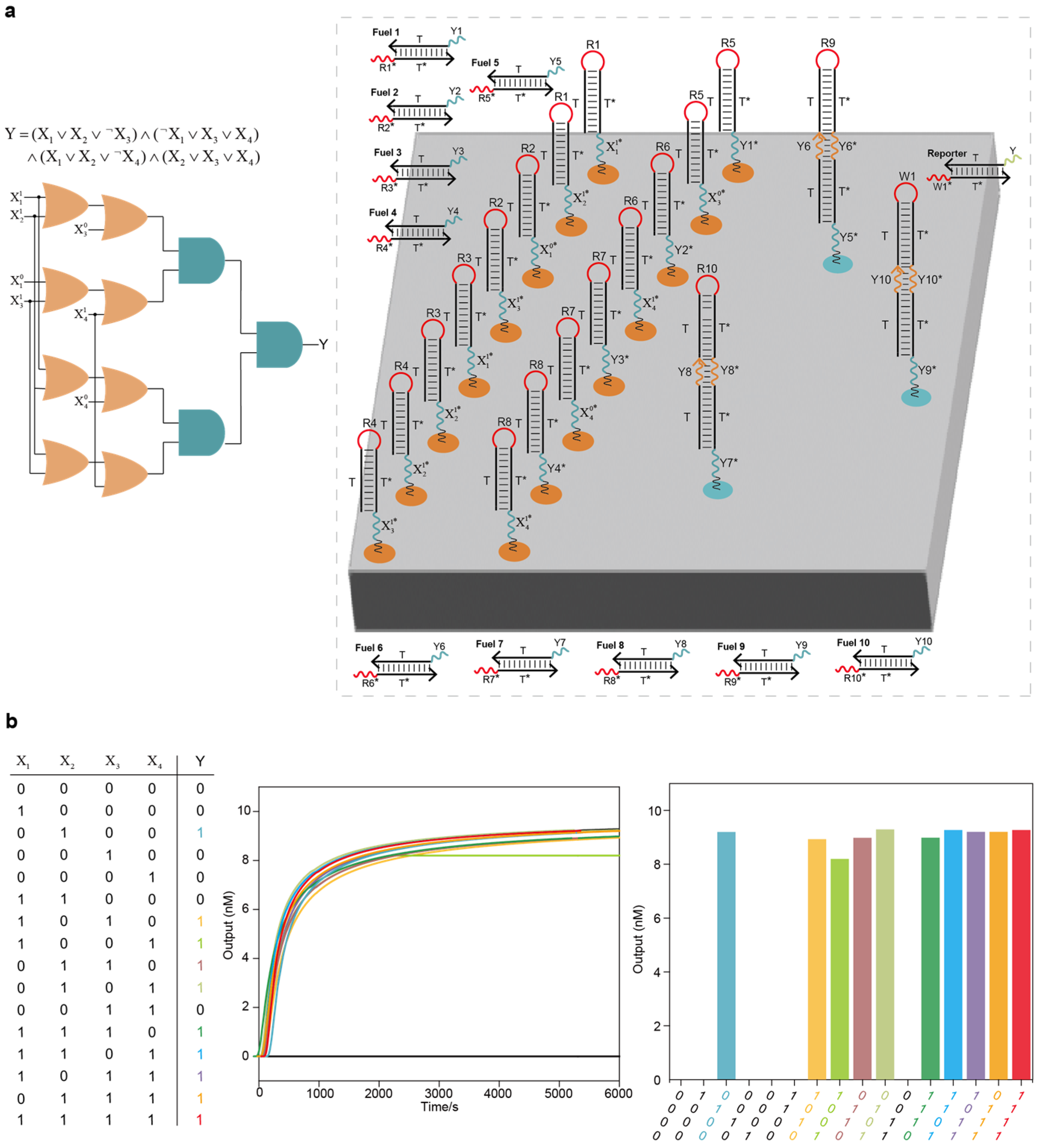
    Integrated DNA logic circuit system for solving the 3-SAT problem: (a) The 3-SAT problem with 4 variables and the layout of the integrated DNA logic circuit system on the DNA origami surface. The entire system had 4 layers, including 8 OR circuits, 3 AND circuits, 10 fuel strands and 1 reporter molecule. (b) Test results under all input combinations using Visual DSD software. There were 10 solutions to this 3-SAT problem in the data pool of 16 possible solutions.

    Figure 5.
    Integrated DNA logic circuit system for solving the 3-SAT problem: (a) The 3-SAT problem with 4 variables and the layout of the integrated DNA logic circuit system on the DNA origami surface. The entire system had 4 layers, including 8 OR circuits, 3 AND circuits, 10 fuel strands and 1 reporter molecule. (b) Test results under all input combinations using Visual DSD software. There were 10 solutions to this 3-SAT problem in the data pool of 16 possible solutions.

    Ijms 26 02043 g005
    Figure 6.
    Localized DNA logic circuit systems for disease classification: (a) A decision tree model for GCT classification based on miRNA expression data of GCT samples from TCGA and the random forest algorithm. (b) The decision tree model mapping into the logic circuit system. (c) The layout of the localized DNA logic circuit system for GCT classification. (d) Confusion matrix analysis of the 87 samples. (e) Testing of the GCT classification for all 25 randomized samples showed agreement between the actual disease states labeled in TCGA, the random forest model and the constructed localized DNA logic circuit system.

    Figure 6.
    Localized DNA logic circuit systems for disease classification: (a) A decision tree model for GCT classification based on miRNA expression data of GCT samples from TCGA and the random forest algorithm. (b) The decision tree model mapping into the logic circuit system. (c) The layout of the localized DNA logic circuit system for GCT classification. (d) Confusion matrix analysis of the 87 samples. (e) Testing of the GCT classification for all 25 randomized samples showed agreement between the actual disease states labeled in TCGA, the random forest model and the constructed localized DNA logic circuit system.

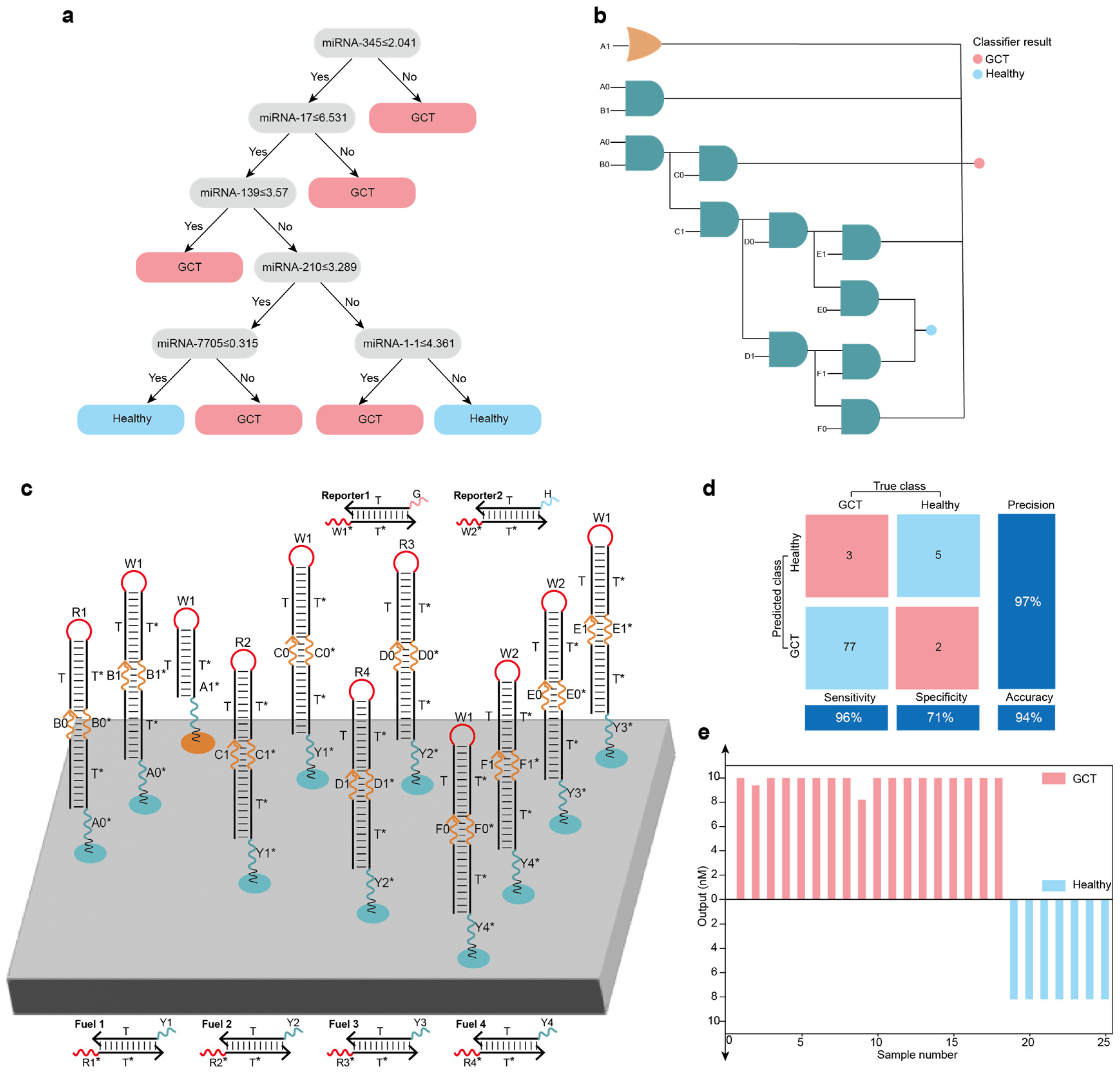
    Ijms 26 02043 g006

    Table 1.
    The main parameters of the Visual DSD simulation programs.

    Table 1.
    The main parameters of the Visual DSD simulation programs.

    SpeciesParameters
    The lengths of all toeholds6 nt
    The lengths of all recognition domains20 nt
    Binding and unbinding rates0.003 s−1 for the binding rate
    0.1 s−1 for the unbind rate
    Directive (defined using the directive keyword and determine how the DSD program should be executed)Simulator deterministic
    Compilation infinite
    Polymers

    Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.



    Source link

    Zhen Tang www.mdpi.com

    Related Posts

    U.S. had its 2nd-warmest October on record
    February 26, 2025
    Simultaneous Removal of Chlorides and Calcium from EAF Dust Wastewater
    February 26, 2025
    Pipeline companies deliver most of the U.S. electric power sector’s natural gas
    February 26, 2025

    Greenberg

    Learn More →
    This website uses cookies to improve user experience. By continuing to use the site, you consent to the use of cookies.