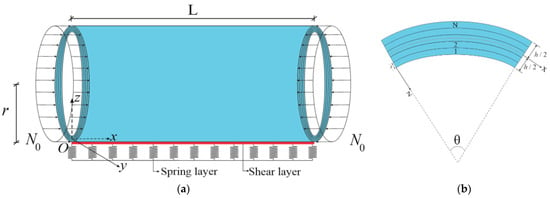
5.1. Initial Data
This section aims to explain the stability behavior of axially loaded cylindrical shells consisting of FG nanocomposite layers resting on the two-parameter elastic foundation and in thermal environments within the FOST and CT based on numerical analysis and interpretations.
The effective material properties of two-phase composites consisting of the mixture of CNTs and PMMA, whose short name is poly (methyl methacrylate), are estimated according to the modified extended rule of the mixture rule method. The PMMA properties in each layer are as follows:
and
. At the reference temperature,
[
26,
33]. (10, 10) armchair single-walled carbon nanotubes (SWCNTs), with properties
in each layer, are used as reinforcements, and the temperature-dependent material properties in the layers are evaluated as follows:
The magnitudes of the material properties and thermal expansion coefficients for
of (10, 10) SWCNTs using Equation (25) are tabulated in
Table 1.
The efficiency parameters
are determined from the extended rule of the mixture method, and molecular dynamics simulation techniques were taken from the studies of [
16,
17,
18,
19], which are tabulated in
Table 2. Since both PMMA/CNT and poly{(
m-phenylenevinylene)-
co-[(2,5-dioctoxy-
p-phenylene) vinylene]} (PmPV)/CNT nanocomposites are used in the comparisons, the efficiency parameters of both are given in
Table 2. At
, the Young modulus of PmPV is
, and other properties are the same as PMMA. The posteriori specified shape functions are defined by
[
8].
5.2. Validation and Verification
In this subsection, the accuracy of the formulas obtained analytically is verified by comparing them with the results obtained using different theories and solution methodologies. The magnitudes of the axial buckling load of unconstrained single-layer cylindrical shells modeled with U- and X-shaped CNTs are listed in
Table 3 for a comparison with the results of Shen [
26] in thermal environments. It should be emphasized that in Shen’s study [
26], Reddy’s higher-order shear deformation theory (HOST) is used [
9]. A comparison was made with Shen’s study [
26]. Since the axial buckling load in thermal environment is used as
in Ref. [
26], expression (24) in our study is multiplied by
at
The shell characteristics are
,
[
26]. The elastic and thermal properties of the nanocomposite containing PMMA/CNT at different temperatures are presented in
Table 1 and
Table 2. As can be seen from
Table 3, the minimum values of the axial buckling load of the U- and X-shaped CNT cylindrical shells within FOST obtained in our study at
T(K) = 300, 500, and 700 are in good agreement with the results of Shen [
26]. The numbers in parentheses
are the wave numbers.
The axial buckling load of the single-layer cylindrical shell panels consisting of FG nanocomposite material with the X shape on the elastic foundation and in thermal environments within the ST is compared with the results of Shen and Xiang [
36] who used the HOST proposed by Reddy [
9] in
Table 4. The dimensionless ground coefficients are defined as
and geometric data are , and [36]. Since the axial buckling load on the elastic foundation and in thermal environments is used as in Ref. [36], expression (22) in our study is multiplied by . The elastic and thermal properties of the nanocomposite containing PMMA/CNT at = 300, 400, and 500 are presented in Table 1. A comparative assessment of the results is presented in Table 4. The good agreement between our results and the predictions in the literature confirms the robustness and accuracy of the proposed formulation.
Table 5 compares the nondimensional axial buckling load (
) of the uniaxially loaded laminated flat panel consisting of U nanocomposite material (PmPV/CNT) plies with the (0°/90°/90°/0°) stacking sequence without elastic foundation with the results of Lei et al. [
37] and Chakraborty et al. [
38] using different solution methodologies for different
, and the necessary parameters are set to be (
). It is seen that our results are in good agreement with the results of Lei et al. [
37], who used the FOST and the meshless kp-Ritz method, and with the results of Chakraborty et al. [
38], who used the HOST proposed by Reddy [
9].
The unique micromechanical model developed for laminated FG nanocomposite (PMMA/CNT) cylindrical shells is applied to investigate the nondimensional axial buckling load values depending on the variation in parameters such as soil, material, shear stress, temperature, stacking sequences, and geometry together and separately:
Since the wave number in the
direction is equal to one (
), it is not included in the tables. The shells with (0°) or SL
1, (0°/90°/0°) or L
31, (90°/0°/90°) or L
32, (0°/90°/90°/0°) or L
41, or (90°/0°/0°/90°) or the L
42 array are used in the next step (
Figure 3).
5.3. Parametric Study
In this subsection, the influences of various factors such as layer arrangement and number, pattern models in each layer, thermal environment, and elastic foundation on the axial buckling load in the framework of classical and shear deformation theories are discussed.
Table 6,
Table 7 and
Table 8 and
Figure 4,
Figure 5,
Figure 6 and
Figure 7 represent the influence of the
on the magnitudes of the
and corresponding circumferential wave number (
) for four types of laminated cylindrical shells with U-,
-, and X-shaped layers with and without elastic foundations in thermal environments within the FOST and CT. In this parametric study, the ST is used instead of the FOST. The necessary parameters are set to be
,
. The values of the nondimensional axial buckling load reduce as the
and
increase with and without an elastic foundation. In all
(=20, 30, 40, 50) ratios, as the values of the nondimensional axial buckling load in the grounded and groundless cases are compared at
= 300, 500, and 700, the presence of the ground significantly weakens the influence of the patterns on the nondimensional axial buckling load values within the ST and CT. In addition, when we examine the groundless and grounded cases within themselves for the fixed
and
,
+ 200 and
+ 400, the influences of the
and X shapes on the nondimensional axial buckling load values generally weaken with the increase in
.
As the
ratio rises from 20 to 50 in the grounded and groundless cases and these are compared with each other at
= 300, 500, and 700, the significant pattern effects on the
occur at different temperatures and alignments within the ST. For example, the most significant pattern effect on the nondimensional axial buckling within the ST occurs in the L
41 alignment shell with the
-shaped plies (−38.65%) in the case without soil at
= 500 and
= 50, while in the case with soil, that influence occurs in the L
31 alignment shell with the
-shaped plies (−35.57%) at
T0(K) = 300 and
= 30 in the case with soil (see
Figure 4a,b also).
With the increase in the
from 20 to 50, the influence of shear deformations on the
of all lay-up shells reduces, while the presence of soil supports reduces that decrease, considering that the increase in temperature weakens that decrease. When the
values of laminated shells in the
= 20, 30, 40, and 50 ratios are compared with each other in the grounded and groundless cases at
= 300, 500, and 700, the pronounced shear stress influences occur in the L
31 array shell in U,
, and X shapes at all values of
in ground and groundless cases (except for U shape, where it occurs in the L
41 array shell for
= 30 and 50). It is noted that most pronounced shear stress influences on the nondimensional axial buckling load occur in the L
31 array shell with X-shaped plies at
= 700 for
= 20. That influence is (+%82.5) in the case without a foundation, while the shear stresses effect on the
weakens by 2.02% in the presence of the elastic foundation (see
Table 6,
Table 7 and
Table 8 and
Figure 5 also).
As the
increases from 20 to 50, significant array effects occur at different
values but in the same arrangements when comparing the values of the
for all layered shells with the
values of the SL
1 shell with and without soil. For instance, the most significant array influence on the
occurs at the X shape (−61.8%) for
= 700 and the L
32 arrangement at
= 30 in the case without soil, while that influence occurs at the X shape (−55.9%) at
and L
32 arrangement at
= 20 in the case with soil within the ST (see
Figure 6 also).
In the grounded case and different
, as the nondimensional axial buckling load values for
= 500 and 700 are compared with the reference temperature (at
), the temperature influences on the nondimensional axial buckling load values for
= 20 and 30 are similar, while those influences for
= 40 and 50 differ according to the layer arrangement and shapes. For example, at
= 500 and 700, the most pronounced temperature effect at
= 20 occurs in the cylinder with the L
31 stacking sequence with U and X shapes, while it occurs in the cylinder for the L
32 stacking sequence with the
shape. At the same temperatures, the most pronounced temperature influence for
= 30 is observed in the L
32 array shell with U and
shapes, while it occurs in the L
31 array shell for X shapes. For
= 500 and
= 40, the most pronounced temperature influence occurs in the shell with the L
31 arrangement at the U,
, and X shapes. For
= 500 and
= 50, the most significant temperature influence occurs in the L
42 shell arrangement in U and X shapes (see
Figure 7 also), while it occurs in the cylinder with the L
32 arrangement in the
shape. For
= 700 and at
= 40 and 50, the most pronounced pattern influence in the U,
, and X shapes in the grounded condition always occurs in the L
32 arrangement cylinder (see
Figure 7 also).