Electrostatic solitary waves (ESWs) occur frequently in space plasmas, for example, planetary magnetospheres, solar wind, Lunar wake, etc. It was shown for the first time by Matsumoto et al. [1] that the broadband electrostatic noise (BEN) observed in the plasma sheet boundary layer by the Geotail spacecraft was composed of a series of bipolar pulses of electrostatic solitary waves (ESWs). After this discovery, the presence of ESWs was reported in the Earth’s magnetosheath [2,3,4,5,6], at the magnetopause [7,8], in the plasma sheet and polar cap boundary layers [9,10,11], on the auroral field lines [12,13,14,15,16], in outer radiation belts [17,18], in reconnection regions in the magnetotail [19,20,21,22,23,24], in solar wind plasma [25,26,27], and in the shock regions [28,29,30,31,32,33].

According to phase space hole models, small-scale holes in the electron or ion phase space give rise to positive- or negative-potential ESWs, respectively. Phase space holes are the Bernstein–Greene–Kruskal (BGK) modes which are generated during the nonlinear stage of some plasma instabilities, such as electron beam–plasma instability, two-stream instability, lower-hybrid instability, and Buneman instability [1,34,35,36,37]. The velocities of the electron holes (EHs) and ion holes (IHs), both observed and predicted by theoretical/simulation models, are found to be of ∼electron thermal velocity and ion thermal or ion-acoustic speed, respectively [1,3,9,10,13,14,36,38,39]. Support for electron (ion) phase space models for ESWs has come from the observations of the Cluster and MMS spacecraft [40,41,42,43,44]. Alternatively, according to nonlinear fluid (solitons) models, ESWs represent density enhancements or depletions generated by electron- and ion-acoustic instabilities [45,46,47,48,49,50,51,52]. In these models, the velocities of ESWs correspond to various electron- and ion-acoustic solitons supported by the plasma system. Lakhina et al. [53,54] have given an excellent review of the applications of nonlinear fluid modes to ESWs observed in space plasmas.

Observations by Cluster at the magnetotail reconnection site [24] and PSBL [55] show the presence of positive-potential slow electrostatic solitary waves (SESWs) with velocities close to ion thermal/ion-acoustic speeds. According to Norgren et al. [55], these ESWs are slow electron holes (SEHs) generated by the Buneman instability driven by a relative drift velocity between electrons and ions of ∼7000 km s⁻¹. However, during SESW events, the Cluster spacecraft did not observe such a large relative drift velocity [55]. Similar SEHs have been also observed in plasma sheet [56] and magnetosheath [57] regions by the Magnetospheric Multiscale (MMS) spacecraft. Kamaletdinov et al. [56] observed a large numbers of SEHs with speeds clustered near a local minimum of contra-streaming ion velocity distribution functions, which is needed to avoid the self-acceleration of SEHs [58]. Shaikh et al. [57] analyzed 645 magnetosheath solitary waves observed by the MMS spacecraft. They found that except for 15 structures, they all had positive polarity, half-widths of 1–10 Debye lengths, and amplitudes between 0.01 and 1.0% of electron temperature. They interpreted these ESWs as SEHs as their typical flow speeds in the plasma frame were ∼100 km s⁻¹ along B. They also found the electron drift speed relative to ions to be much less than the threshold value to excite either the Buneman or the ion-acoustic instability.

Kakad et al. [59] put forward a model, based on analytical nonlinear fluid theory as well as simulations, for the SESWs observed in the PSBL by Norgren et al. [55]. They considered the PSBL plasma region to be a magnetized four-component plasma comprising cold and hot electrons, and cold and hot protons. Three types of nonlinear waves, namely, slow ion-acoustic, fast ion-acoustic, and electron-acoustic waves, were predicted by the analytical model. The fluid simulations not only confirmed the existence of these waves, but also predicted an additional Buneman mode. The Buneman mode had a negative potential, while the other three modes were positive-potential structures. After carrying out a detailed comparison of the observed properties of SESWs and predictions of their model, Kakad et al. [59] concluded that the PSBL SESWs were slow ion-acoustic solitons.

Here, we develop a nonlinear kinetic-fluid model to explain the SESWs observed by MMS1 on 4 August 2017, when the MMS spacecraft were in the plasma sheet at a distance of 20 Earth radii from the Earth [56]. The properties of plasma sheet ESWs observed by the MMS spacecraft, as reported by Kamaletdinov et al. [56], are as follows: typical electric fields $E_{\Vert }$ of ∼10 mV m⁻¹; widths W of ∼a few to a few tens of ${\lambda }_D$ (Debye length); electrostatic potentials $\varphi$ of ∼10 V; and speeds $V_s$ of $\sim -700$ km s⁻¹ opposite to the $\mathbf{B}$ direction. The observed plasma parameters at the time of the ESWs were as follows: core protons with density of $N_c=0.94$ cm⁻³, temperature of $T_c=1700$ eV, and drift velocity of $V_c=105$ km s⁻¹ parallel to $\mathbf{B}$; beam protons with density of $N_b=0.31$ cm⁻³, temperature of $T_b=500$ eV, and drift velocity of $V_b=-1120$ km s⁻¹ opposite to $\mathbf{B}$; hot electrons with density of $N_h=1.25$ cm⁻³ (this is plasma density), temperature of $T_h=500$ eV, and nearly zero drift velocity, i.e., $V_h\sim$0 km s⁻¹. The properties of nonlinear ion-acoustic waves propagating along the magnetic field are studied by employing a hybrid model based on the Sagdeev pseudopotential technique [60] where core and beam protons are treated as adiabatic fluids and the hot electrons kinetically have a vortex-like velocity distribution [61]. We would like to point out that the Sagdeev pseudopotential technique [60] is applicable to the system when all the electrostatic instabilities have stabilized. Therefore, it is not possible to identify which were the initial free-energy sources which drive the instabilities leading to trapping of electrons in the waves. In fact, the Sagdeev pseudopotential method gives the nonlinear eigenmodes of the system when the free-energy sources and instabilities are saturated. Since we use the exact observed plasma parameters as input to the theoretical model, we can predict the final outcome. Four types of modes are predicted by the model, i.e., two fast ion-acoustic (FIA1 and FIA2) solitons propagating along and opposite to $\mathbf{B}$, respectively, and two slow ion-acoustic (SIA1 and SIA2) solitons both propagating opposite to $\mathbf{B}$. It will be shown that the properties of SIA1 and SIA2 solitons match very well with the properties of SESWs observed by the MMS spacecraft.

The hot electrons become trapped in the wave potential of the ESWs during their interaction. The hot electron distribution is considered to be a kinetic vortex-type velocity distribution [61,62,63]:

where v and $\varphi$ are the normalized velocity and potential, respectively. The velocity is normalized with the hot electron thermal speed $v_{th}=\sqrt{T_h/m_e}$, whereas the normalized potential $\varphi =e\Phi /T_h$ (e, $\Phi$, and $m_e$ are the electronic charge, electrostatic potential of the ESW, and mass of the electron, respectively). The shape of the distribution function is controlled by the trapping parameter, $\beta$; e.g., Equation (1) will reduce to a shifted Maxwellian or a flat-top distribution, respectively, for $\beta$ = 1 or 0. On the other hand, Equation (1) represents a situation with a deficit of trapped electrons in the wave potential for $\beta <0$. In the presence of trapped electrons, the normalized electron number density is obtained by integrating Equation (1) and is given by

where

and the error function, $erf\left(\varphi \right)$, and Dawson function, $W_D\left(\varphi \right)$, are defined by

It is to be noted that densities are normalized with total plasma density $N_0$. In the limit $\beta \to 1$, the Boltzmann–Maxwell equilibrium for hot electrons can be retrieved. The case where either $\beta >0$ or $(\beta <0)$ represents a vortex-like distribution. We shall consider the case of $\beta >0$ in Equation (2) corresponding to hot electrons trapped in an arbitrary large amplitude wave; then, the normalized density for electrons can be written as [61,64]:

where $erfc\left(\varphi \right)=1-erf\left(\varphi \right)$ is the complementary error function.

The dynamics of the core and beam protons are governed by the multifluid equations. Following the procedure outlined in Lakhina et al. [49,53,54], we study the ion-acoustic waves propagating along the magnetic field and transform these equations to a stationary frame, i.e., $\xi =(x-Mt)$, where $M=V/C_s$ is the Mach number, which is normalized phase speed of the ESWs. Here $C_s={(T_h/m_p)}^{1/2}$, where $m_p$ is the proton mass. The energy integral is obtained by solving for perturbed densities of core and beam protons, putting core proton, beam proton, and hot electron densities in the Poisson equation, and using appropriate boundary conditions for the localized disturbances along with the conditions that $\varphi =0$ and $d\varphi /d\xi =0$ at $\xi \to \pm \infty$, and is written as [53,61,65,66]:

The Sagdeev pseudopotential, $S(\varphi ,M)$, is given by [49,61,67]

The motion of a pseudo-particle of unit mass in a Sagdeev pseudopotential $S(\varphi ,M)$ where $\varphi$ and $\xi$ represent the displacement from the equilibrium and time, respectively, is described by Equation (5). Equation (5) predicts periodic ion-acoustic waves and solitary ion-acoustic waves as shown by Sagdeev [60]. However, under certain conditions satisfied by the Sagdeev pseudopotential $S(\varphi ,M)$ as stated below, ion-acoustic stable solitary wave or “soliton” solutions are possible [52,54,60,68]. The following are the conditions to be satisfied by $S(\varphi ,M)$ to yield ion-acoustic soliton solutions: $S(\varphi ,M)=0$, $dS(\varphi ,M)/d\varphi =0$, and $d^{2}S(\varphi ,M)/d{\varphi }^2<0$ at $\varphi =0$; $S(\varphi ,M)=0$ at $\varphi ={\varphi }_0$; and $S(\varphi ,M)<0$ for $0<\left|\varphi \right|<|{\varphi }_0|$, where ${\varphi }_0$ is the maximum soliton amplitude [52,54,60,68]. From Equation (6), it is noted that both $S(\varphi ,M)$ and its first derivative, d$S(\varphi ,M)$/d$\varphi$ vanish at $\varphi$ = 0. Further, at $\varphi =0$, the condition $d^{2}S(\varphi ,M)$/d${\varphi }^2<0$ is fulfilled when $M>M_0$, where $M_0$ is the critical Mach number which satisfies the following equation:

We obtain four roots from Equation (7), which is solved numerically for critical Mach numbers, $M_0$.

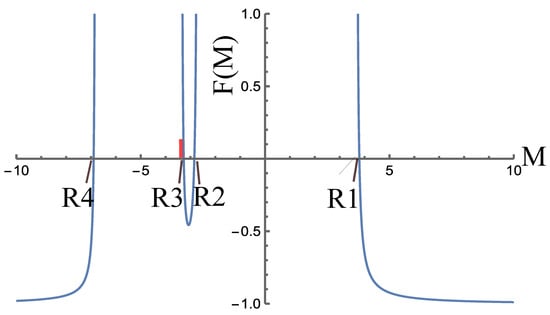
The variation in $F\left(M\right)$ with M is shown in Figure 1 for the normalized parameters of the plasma sheet region, as reported by Kamaletdinov et al. [56]: $n_{c0}=0.75$, $n_{b0}=0.25$, ${\sigma }_c=3.4$, ${\sigma }_b=1.0$, $v_{c0}=0.48$, and $v_{b0}=-5.09$. We obtain four real roots, R1, R2, R3, and R4, as shown in Figure 1, which represent the critical Mach numbers. The roots R1 ($M_0=3.79$) and R4 ($M_0=-6.89$) correspond to the fast ion-acoustic (FIA1) and (FIA2) modes propagating parallel and anti-parallel to $\mathbf{B}$, respectively. Further, roots R2 ($M_0=-2.845$) and R3 ($M_0=-3.271$) correspond to the slow ion-acoustic modes (SIA1) and (SIA2) propagating anti-parallel to $\mathbf{B}$. It is seen that both roots R2 and R3 occur close to the minimum of the proton VDF, shown as a short vertical red line.

Figure 2 shows the Sagdeev pseudopotential $S(\varphi ,M)$ (panel a) electrostatic potential $\varphi$ (panel b), and electric field E (panel c) of the slow ion-acoustic (SIA1) solitons determined from Equations (5) and (6) for the normalized parameters of the plasma sheet given in Figure 1 and for the case of trapping parameter $\beta$ = 0.5. Curves 1, 2, 3, and 4 in panel (a) show the variation in Sagdeev pseudopotential $S(\varphi ,M)$ versus the electrostatic potential $\varphi$ corresponding to the Mach numbers M = −2.87, −2.88, −2.9, and −2.91, respectively. The SIA1 solitons have positive potentials, and the maximum electrostatic potential ${\varphi }_0$ increases with an increase in the Mach number, M, as is obvious from curves 1, 2, and 3. There is no soliton solution for curve 4, which is an indication of an upper limit on M, say, $M_{max}$, beyond which the existence of slow ion-acoustic solitons is ruled out. The variation in SIA1 electrostatic potential $\varphi$ versus $\xi$ is shown in panel (b) for the same Mach numbers M for curves 1, 2, and 3 as in panel (a). It is obvious from the curves that with an increase in M, the amplitudes and widths of the SIA1 solitons tend to increase and decrease, respectively. The corresponding electric field profiles are shown in panel (c) and show a bipolar structure.

Figure 3 shows the properties of slow ion-acoustic (SIA2) solitons which propagate anti-parallel to $\mathbf{B}$ for $\beta =0.5$ and other plasma parameters of Figure 1. The slow ion-acoustic solitons, SIA2, have positive potentials, and the maximum electrostatic potential ${\varphi }_0$ increases with a decrease in the Mach number, M (see curves 1, 2, and 3). In this case, there is a minimum value for M, say, $M_{min}$, below which soliton solutions do not exist (refer to curve 4). The existence of a new class of slow ion-acoustic solitons below the critical Mach number, $M_0$, has been pointed out by researchers [66,69]. The corresponding electrostatic potential and electric field profiles are shown in panels (b) and (c) of Figure 3, respectively (refer to curves 1, 2, and 3).

The profiles of fast ion-acoustic (FIA1) solitons which propagate parallel to $\mathbf{B}$ are shown in Figure 4. Panels (a), (b) and (c) show the Sagdeev potential, electrostatic potential, and electric amplitudes of FIA1, respectively. FIA1 solitons have positive potentials. It is seen that with an increase in Mach number (refer to curves 1, 2, and 3), the maximum electrostatic potential ${\varphi }_0$ increases. A soliton solution does not exist for M = 3.84 (panel (a), curve 4) and beyond.

Fast ion-acoustic (FIA2) solitons which have positive potential and propagate anti-parallel to $\mathbf{B}$ are depicted in Figure 5. Curves 1, 2, and 3 show a trend of increasing maximum electrostatic potential with an increase in Mach number. The numerical computations reveal that for M = $M_{max}$ = −6.92 (see curve 4) and beyond, the existence of solitons is ruled out.

In Figure 6, we show the effects of the trapping parameter $\beta$ on the properties of slow ion-acoustic (SIA1) solitons with the Mach number $M=-2.89$. The effect of variation in $\beta$ on the properties of SIA2, FIA1 and FIA2 solitons is found to be similar. From panel (a) of Figure 6, it is clear from curves 1, 2, 3, and 4 that the maximum electrostatic potential ${\varphi }_0$ increases with an increase in $\beta$. Panels (b) and (c) of Figure 6 show that the amplitudes of both $\varphi$ and E increase and their widths tend to decrease with an increase in $\beta$ (cf. curves 1, 2, 3, and 4 of these panels).

The properties of the slow ion-acoustic SIA1 and SIA2 solitons associated with roots R2 and R3, respectively, and the fast ion-acoustic FIA1 and FIA2 solitons corresponding to roots R1 and R4, respectively, are summarized in Table 1. The velocity, V (in km s⁻¹, column 4); width, W (in m, column 5); electric field, E (in mV m⁻¹, column 6); and electric potential, $\varphi$ (in volts, column 7) are presented as un-normalized quantities. Here, the length between the negative and positive peaks of the electric field E profile is defined as the soliton width, W. The mode and its basic feature are described in Columns 1 and 2, respectively. The Mach numbers associated with curves 1, 2, and 3 of the respective figure corresponding to the mode are given in Column 3. Columns 2 and 3 of the Table 1 reveal that except for the fast ion-acoustic FIA1 solitons which propagate parallel to $\mathbf{B}$, the other three solitons, SIA1, SIA2, and FIA2, propagate anti-parallel to $\mathbf{B}$. All modes have positive potentials (refer to column 7). Columns 4–7 of Table 1 show that the electric fields, E, and potential, $\varphi$, are increased and the widths W are decreased with increasing soliton velocity V for the SIA1, FIA1, and FIA2 modes. However, an increase in soliton speed V leads to a decrease in the magnitudes of E and $\varphi$ and an increase in W for the SIA2 mode.

During the observations of SESWs [56], the plasma parameters give a Debye length of ${\lambda }_D$ = 150 m and an ion-acoustic speed of $C_s$ = 220 km s⁻¹ in the plasma sheet region.

From Table 1, we see that all slow and fast ion-acoustic solitons have positive potentials and the electric fields are in the range of E = (0.41–11.8) mV m⁻¹, which agree with the polarity and the electric fields of SESWs observed in the plasma sheet by the MMS spacecraft. Whereas both the slow ion-acoustic SIA1 and SIA2 solitons and fast ion-acoustic FIA2 solitons propagate anti-parallel to $\mathbf{B}$, the fast ion-acoustic FIA1 solitons propagate parallel to $\mathbf{B}$. The slow ion-acoustic SIA1 solitons have $\varphi$, E, W, and V values in the ranges of (4.5–7.7) V, (5–12) mV m⁻¹, (480–810) m, and (−631 to −638) km s⁻¹, respectively. The slow ion-acoustic SIA2 solitons have potentials, electric fields, widths, and velocities in the ranges of (1.1–3.3) V, (0.9–4.5) mV m⁻¹, (560–1280) m, and (−713 to −717) km s⁻¹, respectively. The fast ion-acoustic FIA1 solitons have $\varphi$, E, W and V in range of (1.5–6) V, (1–9.6) mV m⁻¹, (500–1240) m, and (836–843) km s⁻¹, respectively. The fast ion-acoustic FIA2 solitons have potentials, electric fields, widths, and velocities in the ranges of (0.6–2) V, (0.4–2.9) mV m⁻¹, (558–1299) m, and (−1518 to −1521) km s⁻¹, respectively. From Figure 6, it is clear that an increase in the trapping parameter $\beta$ leads to an increase in the amplitudes of both $\varphi$ and E and a decrease in the widths W of slow ion-acoustic SIA1 solitons.

The properties of the plasma sheet SESWs observed by the MMS spacecraft [56] are parallel electric fields $E_{\Vert }$ of ∼10 mV m⁻¹, electrostatic potentials of $\varphi \sim$10 V, widths W of ∼a few to a few tens of ${\lambda }_D$, and speeds $V_s$ of $\sim -700$ km s⁻¹ anti-parallel to $\mathbf{B}$.

From Table 1, it is clear that the predicted values of E = (5–12) mV m⁻¹, $\varphi$ = (4.5–7.7) V, W = (480–810) m = (3.2–5.4) ${\lambda }_D$, and soliton speed V= (−631 to −638) km s⁻¹ for the slow ion-acoustic SIA1 soliton match very well with the observed values of SESWs. The electric field and potentials associated with SIA2 solitons are less than those associated with SIA1 solitons, and therefore, their match with the observations is not as good. However, the speeds and widths of SIA2 solitons are larger than those of SIA1 solitons and thus provide a better match than the SIA1 solitons with the observations. The fast ion-acoustic FIA2 solitons propagate with speed $V\sim -1500$ km s⁻¹ anti-parallel to $\mathbf{B}$, which agrees with the propagation direction, but the speeds are too high. Their widths W = (3.7–8.7) ${\lambda }_D$ match with the observations, but the associated electric fields and potentials are even smaller than those of the SIA2 solitons. The fast ion-acoustic FIA1 solitons propagate parallel to $\mathbf{B}$, which does not agree with the observed properties of SESWs.

ESWs observed by many spacecraft have been found to obey a statistical relationship where the amplitude of their electrostatic potential usually tends to increase with their widths [4,14,40,70]. This amplitude–width relationship of ESWs is opposite to the properties of Korteweg–de Vries (KdV)-type solitons that have larger amplitudes associated with smaller widths [71]. That all weak solitons behave like KdV-type solitons is a misconception that has been prevailing in the space plasma community for the past several decades. Because of this misconception, the generation mechanisms for ESWs based on ion-acoustic or electron-acoustic solitons have been considered unfeasible and have therefore been ignored [4,14,40,70]. It is worth emphasizing that the properties of the arbitrary amplitude ion- and electron-acoustic solitons predicted by the Sagdeev pseudopotential [60] techniques are quite different from the KdV-type solitons. Nonlinear fluid models based on the Sagdeev pseudopotential methods clearly show that the soliton amplitudes can either increase or decrease with their width depending upon the parametric range of the plasma system [72,73]. These results have brought the soliton/double layer models to the forefront of viable models for the generation of ESWs in space plasmas [52,53,54,67,74,75,76,77,78,79,80]. In this paper, we used actual observed data for our theoretical model based on the Sagdeev pseudopotential [60] technique. It just so happens that the plasma parameters fall in the regime where the soliton amplitudes decrease with width, as seen from Table 1.

It is commonly believed that the slow electrostatic solitary waves (SESWs) observed by many spacecraft in the Earth’s magnetosphere [24,32,55,56,57] are slow electron holes (SEHs), but the mechanism by which SEHs are generated is not certain [55,57,58]. Here, we propose slow ion-acoustic solitons as an alternative mechanism for the occurrence of plasma sheet SESWs. A fluid-type model is developed for studying the evolution of nonlinear ion-acoustic waves using the Sagdeev pseudopotential technique in a magnetized plasma comprising core protons, beam protons, and hot electrons. The core and beam protons are characterized by drifted Maxwellian distributions. For hot electrons, we take a vortex-type distribution with a trapping parameter, $\beta >0$, which describes the distribution with trapped electrons. This pertains to the plasma sheet electrons when SESWs were observed by Kamaletdinov et al. [56]. When the exact plasma parameters reported by Kamaletdinov et al. [56] are taken as an input to the model, they yield two types of slow ion-acoustic SIA1 and SIA2 solitons propagating opposite to $\mathbf{B}$, and two types of fast ion-acoustic FIA1 and FIA2 solitons propagating along and opposite to $\mathbf{B}$, respectively. The electric potentials of all four types of solitons are positive, and the soliton electric fields have bipolar structures. However, we can rule out both fast ion-acoustic FIA1 and FIA2 solitons being responsible for plasma sheet SESWs, as the former propagate parallel to $\mathbf{B}$ and the latter have too low an amplitude of E and $\varphi$. It is interesting to note that the Mach numbers of slow ion-acoustic SIA1 and SIA2 solitons occur close to the minimum of the proton VDF as reported by Kamaletdinov et al. [56], as seen from Figure 1.

From Table 1, we notice that slow ion-acoustic SIA1 and SIA2 solitons have electric fields in the range of E = (0.9–12) mV m⁻¹, potentials of $\varphi$ = (1.1–7.7) V, widths of W = (480–1280) m = (3.2–8.5) ${\lambda }_D$, and speeds of V = (−631 to −717) km s⁻¹, which compare very well with the observations of plasma sheet SESWs with parallel electric fields $E_{\Vert }$ of ∼10 mV m⁻¹, electrostatic potential $\varphi$ of ∼10 V, widths W of ∼a few to a few tens of ${\lambda }_D$, and speeds $V_s$ of $\sim -700$ km s⁻¹ anti-parallel to $\mathbf{B}$. However, we would like to point out that a discrepancy by a factor of ∼2 between the width of ESW reported by Kamatetdinov et al. [56] and the predicted widths of slow ion-acoustic solitons (as seen from Table 1) may arise from variations in plasma parameters due to the relative time delay between observations of ESWs and measurements of plasma distributions. Furthermore, the widths predicted by the models (∼3–9 ${\lambda }_D$) are well within the range of SESW widths observed statistically, i.e., a few to a few tens of Debye lengths.

To sum up, slow ion-acoustic SIA1 and SIA2 solitons provide a plausible explanation for the occurrence of parallel propagating slow electrostatic solitary waves in the plasma sheet observed by the MMS spacecraft [56]. We did not conduct an analysis for the negative value of the trapping parameter $\beta$ which describes BGK hole-type solutions for hot electron distributions. Offhand, we cannot rule out the possibility of slow ion-acoustic solitons in this case also. Perhaps the parameters of the ion distributions need to be changed to obtain slow ion-acoustic solitons. We will explore this and report the results elsewhere.