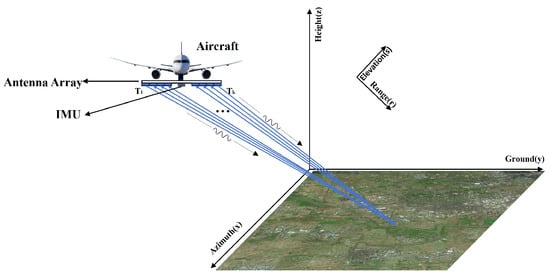
1. Introduction
Airborne array SAR represents an advanced earth observation system [
1]. Compared with traditional single-channel SAR and dual-channel interferometric SAR (InSAR), it can obtain multi-channel echo data via cross-track array antennas [
2]. Therefore, it can achieve the resolution of the third dimensional height and effectively solve the problem of layover and other problems that are not conducive to target interpretation [
3]. Different from the multi-pass tomographic SAR (TomoSAR) technology, the airborne array SAR only needs once flight to obtain multi-channel data for 3D processing, which improves the efficiency of data acquisition and also weakens the influence of time decorrelation [
4]. Benefiting from the great advantages of airborne array SAR technology, it has been widely studied and applied in the fields of disaster assessment [
5], environmental monitoring [
6,
7], and urban and mountain mapping [
8,
9,
10].
Airborne array SAR acquires multi-channel echo data via the multiple-input–multiple-output (MIMO) technique using array antennas [
11]. Because of the slight differences between antenna parameters and internal circuits, as well as the impact of the installation process and the structure of aircraft on the channel echo data, there exists parameter errors among the various channels, mainly reflected in amplitude and initial phase errors [
12]. Since there are many influencing factors that may change over time, it is not possible to accurately calibrate them through static calibration and internal calibration methods [
13]. Additionally, since the electrical phase center of the antenna does not coincide with the geometric location center, it is difficult to find the exact position of the antenna phase center when measuring the actual antenna position, resulting in measurement errors. Therefore, there is a certain error in the equivalent phase-center positions of the various channels. The height resolution of the airborne array SAR system is limited by the length of the antenna, and super-resolution algorithms are needed [
14]. However, super-resolution algorithms are sensitive to various parameter errors [
15]. In order to ensure the resolution in the height direction, the phase-center position is generally required to achieve sub-wavelength accuracy. The amplitude error of each channel is within 0.2 dB, and the phase error is within
. In addition, the phase-center position error and the initial phase error are coupled in the data. Separative calibration makes it difficult to achieve precise results, so it is necessary to calibrate these parameters together to reach higher accuracy.
In the domain of multi-channel SAR error calibration, significant research has also been conducted. In 2014, Yang et al. proposed the amplitude and phase error correction method for an array SAR system based on single special point target echo [
16]. In 2016, Tebaldini et al. calibrated the phase-center positions of the European Space Agency’s AlpTomoSAR by using the phase-center double localization (PCDL) method [
17]. In 2018, Aghababaee et al. used this method to estimate the phase error by optimizing the contrast or entropy of the vertical contour under the constraint of a zero phase derivative [
18]. In 2019, D.Feng et al. proposed a phase calibration method for the multi-channel residual phase error caused by uncompensated platform motion in airborne holographic SAR imaging [
19]. In 2020, Z. Jiao et al. used strong scattering points in two-dimensional (2D) SAR images to complete the amplitude–phase imbalance calibration between channels through two steps of calibration and reconstruction [
20]. In 2021 and 2022, H. Lu et al. designed the NC-PGA and BBN-PGA methods based on network construction and PGA to calibrate and compensate the phase error in multi-channel SAR [
21,
22]. In 2023, D. Wang et al. uesd a new method based on prominent points to calibrate spatially varying amplitude–phase imbalance errors in Airborne array TomoSAR [
23]. In 2024, F.Huang et al. proposed a PGA-based phase error compensation method for HoloSAR to address the vertical shift issue caused by linear phase errors [
24]. In 2024, Y. Cai et al. proposed an efficient method based on least spectrum difference to calibrate multichannel phase error in azimuth multichannel SAR [
25]. However, these methods still have some defects. First, they do not consider all the error parameters and calibrate them together. Furthermore, they only compensate for the errors and do not estimate the error parameters required for imaging. In 2018, Bu et al. used multiple corner reflectors placed on the ground, combined with the maximum likelihood estimation and the least squares method, to calibrate the multi-channel imbalance and phase-center positions of the array TomoSAR simultaneously [
26]. However, the method has poor robustness and cannot be applied when the initial value error is large.
Additionally, as the airborne array SAR operates with array antennas, calibration of parameter errors can draw upon the existing studies of antenna parameter error calibration in array radars. Regarding the calibration of antenna parameter errors in array radars, Weiss A. J et al. proposed a self-calibration method based on subspace fitting in 1989, which can estimate both the position of the antenna elements and the direction of arrival (DOA) of the source simultaneously [
27]. In 1999, Poh B. K et al., based on the maximum likelihood principle, presented a joint solution algorithm capable of estimating mutual coupling, amplitude and phase inconsistencies, phase-center positions, and the DOA of the source simultaneously [
28]. In 2009, Wijnholds et al. combined the maximum likelihood method and the subspace fitting method, proposing a weighted alternating least squares method [
29]. In 2020, Vasanelli et al. obtained multiple relative calibration target measurements through radar rotation, thus calibrating errors caused by amplitude and phase variations and mutual coupling in the channels of MIMO radars [
30]. In 2021, J. Geiss et al. proposed a cost-effective near-field calibration method using a sparse but unknown target scenario for the calibration of complex gain and mutual coupling in radar antenna arrays [
31]. However, the aforementioned methods are all aimed at small sensor array radars with small intervals between antenna arrays and minimal errors in phase-center location. They also only consider the radar in a stationary state, that is, the phase-center position is constant. In airborne array SAR, where the array antennas are moving, the phase-center locations of each channel can change due to motion errors. Additionally, SAR imaging is a comprehensive process that cannot receive multiple snapshots at fixed positions, making multi-channel phase-center calibration more challenging.
In summary, the existing methods cannot be well applied to the current multi-parameter calibration problem of airborne array SAR. Therefore, this paper proposes a multi-parameter calibration method for airborne array SAR based on the Newton method and the genetic algorithm. The method can jointly estimate and calibrate the multi-channel amplitude–phase imbalance error and phase-center position error in the airborne array SAR system. The fast convergence of the Newton method in least squares and the ability of the genetic algorithm to search for global optimization are used in the meantime. The estimation results of each parameter can be obtained efficiently and accurately, which provides a guarantee for the quality of 3D imaging results of airborne array SAR. Simulation experiments and actual data processing results verify the effectiveness of the proposed method.
This paper is organized as follows.
Section 2 introduces the echo signal model and multi-parameter calibration model of airborne array SAR.
Section 3 presents the specific steps of the proposed multi-parameter calibration method. In
Section 4, the simulation experiments are carried out first, then the processing results of actual flight data are shown. Discussions are given in
Section 5.
Section 6 presents the conclusions of the paper.
3. Method
In this section, based on the established least squares model for the multi-parameter calibration of airborne array SAR, the new calibration method based on the Newton method and the genetic algorithm is introduced; the parameters to be estimated are primarily the multi-channel amplitude–phase imbalance and the position of the phase center. Firstly, the nonlinear least squares method for estimating multiple parameters is introduced. In order to enhance iterative efficiency, the Newton method, which utilizes second-order information, is employed. Subsequently, to address the issue of the Newton method requiring high-quality initial parameter estimates, a new solution combined with the genetic algorithm is proposed to improve the stability of parameter estimation.
3.1. The Newton Method
Based on Equation (
12), it is evident that the parameter representing the amplitude–phase imbalance, denoted as
, and the phase-center position parameter, denoted as
, can be iteratively calibrated by employing a stepwise least squares approach. Initially fixing
, the least squares estimate of
is obtained as
Subsequently, substituting
into Equation (
12), the cost function is obtained as
Therefore, the estimation of
is equivalent to minimizing the cost function,
. When the initial value of the phase-center position,
, is sufficiently close to the true value, a second-order Taylor expansion is employed, resulting in the following expression:
where denotes the gradient vector obtained by taking the first derivative of and represents the Hessian matrix acquired by taking the second derivative of . The specific derivation and expressions of both can be found in [32]. When only a first-order term is employed, the least squares iteration is also known as the gradient descent method, and the iterative update quantity is expressed as
where denotes step size and is the norm of the vector. If a second-order term is utilized, the least squares method is referred to as the Newton method, and the iterative update quantity is represented as
The Newton method generally converges faster than gradient descent when it is close to the local minimum due to its quadratic order of convergence. The Newton method uses both the first and second derivative in its calculations. Hence, it estimates the function curvature, leading to potentially larger steps toward the function’s minimum.
According to the above derivation process, the basic steps of the parameter calibration method based on the Newton method in the least squares can be obtained. First, the initial value of the phase-center position,
, is substituted, and then the gradient vector,
, and the Hessian matrix,
, are calculated to obtain the iterative update,
, and update the value
X. Then, the above steps are repeated until the cost function and the parameter estimate converge to obtain the final estimate,
. Finally, the estimation of amplitude–phase imbalance,
, is calculated by nonlinear least squares. The detailed steps of the airborne array SAR multi-parameter calibration method using the Newton method are shown as Algorithm 1. Multi-look processing is the first step of data preprocessing. In array signal processing, multi-snapshot data are commonly used to obtain the estimation of the signal’s array manifold. In array SAR, similar multi-snapshot data of signal sources, as used in array radar DOA estimation, can be acquired by performing frequency domain or image domain multi-look processing on two-dimensional SAR images [
33].
| Algorithm 1: The Multi-parameter Calibration Method for Airborne Array SAR Based on Newton Method |
Input: Multi-channel echo data, initial values of parameters
Initialization: Multi-look processing of multi-channel data and preliminary registration.
Step 1: Extract the multi-channel complex values of each ground control point (GCP) in multi-look images;
Step 2: Estimate the values of the array manifold of GCPs according to the principle of spatial spectrum estimation;
Step 3: Construct the cost function according to Equation (14);
Utilize the nonlinear least squares method for iterative estimation of multiple parameters:
Step 4: Compute the gradient vector, , and the Hessian matrix, ;
Step 5: Employ the Newton method to acquire updated values of multi-channel phase-center positions, ;
Step 6: Calculate the cost function value. If it is less than the predetermined threshold, then terminate the iteration. Otherwise, update and repeat step 4∼6;
Step 7: Utilize Equation (13) to estimate multi-channel amplitude–phase imbalance, ;
Output: The final multi-parameter estimations and . |
3.2. The Genetic Algorithm
The genetic algorithm is a classical intelligent optimization method [
34]. Its fundamental principle is to imitate the evolutionary laws found in nature. The genetic algorithm encodes the parameters of a given problem into chromosomes and then employs iterative operations such as selection, crossover, and mutation to exchange information among the chromosomes within a population, ultimately generating chromosomes that meet the optimization objectives. In the context of the genetic algorithm, chromosomes correspond to data or arrays, commonly referred to as individuals. A specific number of individuals compose a population. The number of individuals within a population is referred to as the population size, while the degree of an individual’s adaptability to the environment is termed fitness. In optimization problems, the calculated value of the cost function is typically treated as the fitness of an individual. The basic flowchart of the genetic algorithm is shown in
Figure 3.
The genetic algorithm is a stochastic global search optimization method that simulates various phenomena occurring in natural selection and genetics. Starting from an arbitrary initial population, it employs random selection, crossover, and mutation operations to generate a group of individuals that are better adapted to the environment, thereby evolving the population towards increasingly favorable regions of the search space. Through this iterative process of evolution across multiple generations, the algorithm ultimately converges to a group of individuals that are most suited to the environment, facilitating the acquisition of high-quality solutions to the problem. The key to the genetic algorithm lies in the selection of coding method, genetic operator, and fitness function. At the same time, the algorithm will also be affected by various parameters. At present, the genetic algorithm has been widely used in combinatorial optimization, machine learning, signal processing, adaptive control, and other fields [
35].
3.3. The New Calibration Method Based on the Newton Method and the Genetic Algorithm
According to the above introduction in
Section 3.1, the Newton method can obtain the optimal parameter estimation by iterative optimization under the condition of a given initial value. However, in certain instances the Newton method can be relatively sensitive to the initial parameter values. It employs the first-order derivative and second-order derivative of the function to locate the optimal points; hence, its performance and ability to converge to a global optimum might be influenced by the choice of initial values. If the initial values are inappropriately chosen, it could result in convergence to local optima. Particularly when there are numerous parameters, the objective function often carries multiple extreme points, and the Newton method may converge to a local optimum instead of to a global one. Moreover, in some situations, if the Hessian matrix near the initial point is not positive-definite, or if the gradient changes steeply, the algorithm may fail to converge.
In summary, when the airborne array SAR system’s parameters contain significant errors, relying solely on the Newton method might not accurately calibrate all parameters. Genetic algorithms can effectively address this issue. Genetic algorithms possess global search capabilities and are not easily trapped in local optima. However, they are less capable of finding precise optimal solutions and typically yield approximate solutions. By leveraging the strengths of both the Newton method and genetic algorithms, one can use genetic algorithms to obtain a good initial solution and subsequently refine it with the Newton method for more accurate optimization, thereby enhancing the robustness of the algorithm. Based on the foregoing analysis, this paper proposes an airborne array SAR multi-parameter calibration method that amalgamates genetic algorithms with the Newton method. The specific details of the entire process are as follows:
Obtain sub-aperture complex images for each channel after multi-look processing of the array SAR multi-channel echo data;
Register multi-channel SLC images for next operation;
Extract the complex values of GCPs in the multi-channel SLC images;
Based on the principles of spatial spectrum estimation, obtain the array manifold estimate via eigenvalue decomposition of the covariance matrix of the observation vector shown in Equation (
10);
Initialize the genetic algorithm by setting the population range according to the initial values of the parameters and establish the population size. Calculate the cost function values corresponding to the parameters of each individual in the population, and then perform genetic iterative operations from steps 6 to 9;
Take the parameters of each individual in the population as initial values, employ the Newton method for nonlinear least squares iterative estimation to obtain new parameter estimates and calculate the corresponding cost function values;
Reorder the individuals in the population based on the cost function values;
Execute selection, crossover, and mutation genetic operations based on predetermined probabilities to obtain a new population;
When the minimum cost function value corresponding to the optimal individual in the population is less than the predetermined threshold, Q, or when the number of genetic iterations exceeds G, the iteration is terminated and the parameter estimate corresponding to the optimal individual in the final population is output.
The overall flow chart of the proposed method is shown in
Figure 4. In the proposed methodology, the selection of parameters for the genetic algorithm plays a critical role. Given the high precision requirements for the parameters to be calibrated, utilizing binary encoding may lead to an excessive number of encoding bits, thereby increasing computational complexity. Consequently, real-valued encoding is chosen to ensure the continuity of the variables. Regarding the selection of population size, the need to perform Newton iterations on each individual after every population update incurs a significant computational cost. However, larger population sizes can enhance the probability of locating the global optimum. Hence, a moderate population size is considered appropriate after careful consideration. The selection and crossover operations employ a monarch scheme to ensure that the best individuals in the population are not lost due to random selection or crossover mutation, thereby improving the convergence speed of the algorithm. In order to achieve rapid convergence, the crossover probability is generally set above 0.7. Additionally, due to the complexity of the fitness function, a relatively high mutation probability, such as 0.1, is recommended to avoid the risk of falling into local optima. Overall, the selection of parameters should be based on the specific situation or determined through multiple trials [
36].
5. Discussion
Simulation experiments and the processing results of actual airborne array SAR flight test data have verified the effectiveness of the method. Initially, in the simulation experiments, the results of a single experiment in
Figure 6 indicated that, when the initial parameter values were significantly different from the true values, the parameter calibration method using the Newton method would fall into local convergence and fail to approach the true values. The parameter calibration method based on the genetic algorithm still had significant errors after multiple iterations. In contrast, the proposed method was not influenced by the initial parameter values, with the calibrated parameter values being close to the true values. Furthermore, by setting random parameter errors and conducting multiple Monte Carlo simulation experiments, comparing the parameter calibration results of the Newton method and the proposed method under the same parameter error conditions, the phase-center position error results after calibration in
Figure 7 showed that the parameter calibration based on the Newton method could be unstable due to parameter errors. The proposed method demonstrated strong robustness, approaching the true values under different parameter error conditions. Subsequently, in the actual airborne array SAR flight test, ground-based corner reflectors were used as GCPs for calibration.
Figure 12 shows that the calibration result based on the Newton method could not converge, whereas the calibration result based on the proposed method was able to converge to a lower level of the cost function, and the authenticity of the result was verified by comparison with interferometric calibration results. Ultimately, the comparison of 3D imaging results before and after parameter calibration in
Figure 13 confirmed the effectiveness of the proposed method.
In summary, the method presented in this paper can effectively calibrate amplitude–phase imbalance and phase-center position errors in airborne array SAR, enhancing the quality of 3D imaging and exhibiting strong robustness when parameter errors are large. Although the proposed method can perform joint calibration of multiple parameters, there are still some tasks to be completed: Firstly, the method assumes that the amplitude–phase imbalance of each channel is a fixed constant, which is reliable in most cases. However, when the inter-channel errors are substantial, particularly when the antenna pattern errors are significant, the amplitude–phase imbalance may exhibit spatial variability, causing the model to fail and resulting in significant errors, even after calibration. Secondly, the method relies on ground control points, and when the number of channels is large the number of control points also increases, making the study of calibration methods without control points equally important. Finally, the method also receives the influence of SNR. How to ensure the calibration accuracy in the case of low SNR is also a problem.
6. Conclusions
The airborne array SAR system is capable of achieving 3D imaging of the observed scene. However, affected by various instability factors, the system also contains various error sources of SAR and array antenna. Under the influence of parameter errors, the quality of the 3D imaging results of the airborne array SAR system deteriorates, resulting in a large number of spurious points in the final point cloud output. The error parameters that significantly affect imaging are mainly multi-channel amplitude–phase imbalance and the phase-center position. The phase errors caused by phase imbalance and phase-center positional errors are coupled together, making separate calibrations less accurate. Therefore, to address the above issue, this paper proposes a multi-parameter calibration method for airborne array SAR based on the Newton method and genetic algorithms. By combining the fast convergence of the Newton iterative method in the nonlinear least squares and the global optimization capability of genetic algorithms through complementary advantages, it enables rapid and accurate effective calibration of multiple parameters. Simulation experiments compared the calibration results of the proposed method with other methods. The results of single simulations and multiple Monte Carlo simulations both demonstrated the superiority of the proposed method. Furthermore, experiments with real airborne flight data have shown that the proposed method can effectively calibrate multiple parameter errors in the airborne array SAR system, enhancing the quality of 3D imaging. Simulation and real-data experiment results confirm the robustness of the proposed method, which maintains good calibration accuracy even when parameter errors are significant, making it of great importance for ensuring high-resolution and high-precision imaging in airborne array SAR systems. In the future, we aim to provide more universal calibration methods for a wider range of applicable scenarios, such as distributed arrays, among others.