A Simple Framework for Contrastive Dictionary Learning

1. Introduction

Dictionary learning (DL) is a branch of signal processing and machine learning that aims to find a frame (or dictionary) for sparsely representing signals as a combination of few elements. The initial basis is unknown and is usually learned from the data. This method has been widely used in multiple fields, such as image and audio processing, inpainting, compression, feature extraction, clustering, and classification.

The DL problem can be formulated as follows:

$\begin{matrix} min_{D, X} & {∥ Y - D X ∥}_{F}^{2} \\ s . t . & {∥x_{ℓ}∥}_{0} \leq s, ℓ = 1 : N \\ ∥d_{j}∥ = 1, j = 1 : n, \end{matrix}$

(1)

where $Y \in R^{m \times N}$ is the matrix that contains N signals of size m, stored compactly as columns, $D \in R^{m \times n}$ is named dictionary and is usually overcomplete ( $m < n$ ), and $X \in R^{n \times N}$ is the coefficients’ matrix. The column vectors of matrix $D$ are named atoms and define the basis vectors used for the linear combination. For each signal sample, only s atoms are used for the representation. The matrix $X$ is a sparse matrix that contains the coefficients associated with the atoms used for the linear representation.

The DL problem is typically solved in two optimization stages: dictionary update and sparse coding. At the beginning of the algorithm, the dictionary

D

is randomly initialized with normalized atoms; random initialization does not favor obtaining the best results, but satisfactory results can still be obtained. In the sparse coding stage, the dictionary is considered fixed and all sparse coefficients (the elements of the matrix

X

) are computed for each sample signal. A popular method for sparse coding is Orthogonal Matching Pursuit (OMP) [1]. This greedy algorithm selects the atoms sequentially based on their correlation with the residual representation. In the next stage, the dictionary matrix,

D

, is updated, while the coefficient matrix is considered fixed. Several algorithms are available for updating the dictionary matrix [2]. The K-means Singular Value Decomposition (K-SVD) [3] and Approximate K-SVD (AK-SVD) [4] are among the most used update algorithms. The optimization continues by alternating between these two stages until a stopping criterion is met. In general, two different criteria are used: the maximum number of iterations or the representation error dropping off under a threshold value.

Dictionary learning (DL) can be used in various application problems. Considering the sparse representation capabilities and the light optimization procedure, relevant results can be obtained in practice. However, performance usually depends on the initialization of the dictionary and its properties. For example, in classification problems or discriminative learning, the incoherence of the atoms becomes relevant. Incoherence is the property of the atoms to be far apart one from another; equivalently, their scalar product is small in absolute value. Several methods include discriminative terms in the optimization procedure to meet the incoherence goal. On the other hand, a pre-trained dictionary can be advantageous when prior knowledge about the data is known. In this paper, we address the dictionary initialization problem using a previous problem validated for deep neural networks in a self-supervised manner. This initialization can be used for general problems or classification problems solved with DL.

Contrastive learning is a method that aims to learn similar and dissimilar representations from the data. This method can be used in supervised problems with known sample labels. However, the discrimination problem becomes untractable when dealing with large datasets. A straightforward method for learning instance discrimination is the use of categorical cross-entropy loss. As the dataset increases in size, performing the softmax operation to calculate class probabilities becomes excessively costly. The challenge of using categorical cross-entropy loss, such as discrimination, lies in its computational infeasibility when dealing with large datasets. Researchers have been searching for more efficient ways to approximate this loss. Recent advances are inspired by metric learning, as well as the work in [5,6].

A significant challenge within the instance discrimination framework is the lack of intraclass variability. In traditional supervised learning, there are typically hundreds or thousands of examples per class, which helps the algorithm to learn the inherent variation within each class. However, in many applications, there are only a few examples per class, which clearly hinders the learning process. This issue can be tackled through extensive data augmentation. By applying different transformations to a specific data point, we can generate slightly varied versions while maintaining its fundamental semantic meaning. This approach allows us to learn valuable representations without relying on explicit labels.

To set up the contrast between instances, several views of the inputs are produced using a process $T$ and then evaluated in the representation space. For a particular input $y_{i}$ , an anchor is calculated as $y^{(a)} \sim T (y_{i})$ and then compared to a positive sample $y^{(p)} \sim T (y_{i})$ , which is another transformation of the same input or a sample from the same class with the anchor. A negative sample, $y^{(n)} \sim T (y_{j})$ , which represents a transformation of a different input, is also contrasted with the anchor. In addition, the process $T$ is modified or updated so that it represents positive pairs in a compact form, while negative pairs are projected far apart.

In the general context of Self-Supervised Representation Learning (SSRL), this approach involves a pretext task generator $P$ that creates pretext inputs for multiple pairs of raw input instances. These inputs have pseudo-labels that indicate whether the pairs are matching or not.

The anchor and positive and negative samples are then processed by a feature extractor

h (\cdot)

to derive their respective representations:

x^{(a)} = h (y^{(a)})

for the anchor,

x^{(p)} = h (y^{(p)})

for the positive sample, and

x^{(n)} = h (y^{(n)})

for the negative sample. After this, a similarity function denoted by

Φ

is used to evaluate the similarity between pairs of projections. The whole model is subsequently trained to minimize the distance between positive pairs and to maximize the distance between negative pairs. A simple formulation of contrastive learning loss is formulated as follows:

$L_{con} = - E [log \frac{Φ (x^{(a)}, x^{(p)})}{Φ (x^{(a)}, x^{(p)}) + \sum_{j = 1}^{k} Φ (x^{(a)}, x^{(n)})}],$

(2)

where k represents the number of negative samples that have been used in contrast with the anchor. The training process can also include the transformation process $T$ or only the encoder $h (\cdot)$ .

Multiple versions of this strategy can be employed within this framework. The methods vary based on the similarity function, the family of transformations $T$ , the encoder function $h (\cdot)$ , and approaches to the sampling anchor, and positive and negative examples.

There are many unsupervised applications [7] that have been developed in the spirit of Self-Supervised Representation Learning (SSRL). These methods enable the development of generalizable models that have the potential to learn and recognize a wide variety of patterns in the data.

Several strategies are available, such as Momentum Contrast (MoCo) [8], Pretext-Invariant Representation Learning (PIRL) [9], and a Simple Framework for Contrastive Learning of Visual Representations (SimCLR) [10]. MoCo is a framework that uses a queue and a moving average encoder to learn visual representations. In PIRL, invariant representations are learned by solving pretext tasks. SimCLR uses a simple contrastive loss function to learn visual representations. The simple contrastive loss is applied by learning similar representations for augmented versions of the same input image while discriminating representations of dissimilar images.

Contributions. In this paper, we adapt the SimCLR framework to the dictionary learning problem, with the purpose of obtaining more incoherent atoms that are better adapted for DL applications (classification and anomaly detection). The learned atoms can then be used to improve sparse representations, leading to smaller representation errors and better discriminative performances.

The main contribution is reconfiguring the initial SimCRL algorithm in the context of dictionary learning. This includes the substitution of the base encoder network with a dictionary learning problem. The network projection head is no longer used since the encoding and projection are performed using the OMP algorithm. The augmentation procedure was adapted for n-dimensional vectors. For this, we only used four elementary operations, which were changed in the context of dictionary learning. This self-supervised framework is capable of building more incoherent dictionaries, which facilitates a better representation error and has an impact on further supervised and semi-supervised applications.

The use of SimCLR can be beneficial for dictionary learning applications from different perspectives. In many real-world applications, large amounts of unlabeled data are used. SimCLR can learn robust feature representations from the unlabeled data, which can then be used to initialize the dictionary. This initialization can improve the performance of downstream tasks, such as classification, anomaly detection, or clustering, even when labeled data are scarce. On the other hand, the initialization of the dictionary using the SimCLR framework can boost the optimization process. The learning process can start from a more informative and structured point, potentially leading to faster convergence and more stable solutions. This not only enhances the efficiency and effectiveness of the learning process, but also improves the interpretability and stability of the resulting model.

The content of this paper is organized as follows. In Section 2, we introduce the self-supervised contrastive framework in the context of dictionary learning. The augmentation methods required for this framework are included in Section 3. In Section 4, we include several algorithms that have been used for our experiments. These algorithms [11] also aim to respect a discriminatory representation using contrastive learning. Our tests demonstrate that the use of the SimCLR framework is beneficial for dictionary learning algorithms that promote contrastive learning. We then continue with the presentations of our experiments in Section 5. We conducted tests on two mainstream tasks, namely classification (Section 5.1) and anomaly detection (Section 5.2). In the last section, we end up with some conclusions.

2. Contrastive Dictionary Learning

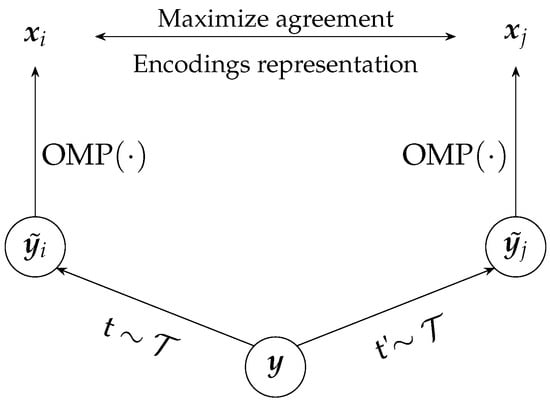
This section explains the Simple framework for Contrastive Dictionary Learning (SimCDL), which is used for dictionary initialization. This framework is developed in the spirit of SimCLR [10], a powerful approach to unsupervised representation learning. At the base of this framework lies the loss function, designed to learn rich and discriminative embeddings from unlabeled data. For the Contrastive Dictionary Learning framework, we consider the same loss function, but we propose a different logic for computing the encodings representation.

In the context of dictionary learning (DL), we apply stochastic data augmentation transformations to generate pairs of correlated signals from the same example, denoted $\tilde{y_{i}}$ and $\tilde{y_{j}}$ . These two samples are derived from an initial sample $y$ . Let $T$ represent the space of augmentation operations that can be applied to the samples. For two different random initializations of the augmentation operators, we have $t \sim T$ and $t^{'} \sim T$ . The next step is to follow an encoding process that aims to maximize the agreement between the two augmented samples in the representation space.

The SimCLR problem has been adapted without using a projection head or a base encoder. Instead, the dictionary $D$ is used directly to calculate the encodings using an OMP procedure. The embeddings are represented by the column vectors of the matrix $X$ .

To build a positive pair of encodings, denoted as $x_{i}$ and $x_{j}$ , we compute the representation coefficients of the two augmented samples, $\tilde{y_{i}}$ and $\tilde{y_{j}}$ . In addition, contrastive loss is calculated to measure similarities between positive pairs of encodings and discriminate them from negative pairs.

This setup leverages the principles of SimCLR, primarily contrastive learning, in a sparse coding problem. SimCLR is typically used to learn useful representations by maximizing the agreement between different augmented examples of the same data sample via a contrastive loss in the latent space. An example illustrating the SimCDL steps is shown in Figure 1.

To compute the loss function, we randomly select a mini-batch of K examples at each iteration. After that, we create pairs of augmented samples for each of the K examples, resulting in a total of $2 K$ data points. By doing so, we do not need to sample negative examples explicitly.

Additionally, we consider other augmented examples as negative samples in relation to the positive pair. After this, we calculate an embedding for each augmented sample using the OMP algorithm

$x_{i} = OMP ({\tilde{y}}_{i}, D, s),$

(3)

where $D$ is the dictionary matrix and s is the sparsity level.

OMP aims to find the best sparse representation of a signal by iteratively selecting the most relevant atoms from the dictionary $D$ . Iteratively, the algorithm selects the atom most correlated with the current residual. After the selection is made, the residual is updated by projecting the signal onto the subspace spanned by the selected atoms. This process is repeated until a stopping criterion is met (e.g., a desired sparsity level or error threshold). This whole process substitutes the encoding base network that was previously used in SimCLR.

The similarity of the encodings, obtained with OMP, is computed using the cosine similarity of their normalized feature vectors,

Φ (u, v) = u^{⊤} v / ∥ u ∥ ∥ v ∥

. In contrast, the negative encoding should use other atoms in their sparse representation, leading to incoherent embeddings. The loss for a positive pair of examples is calculated using a softmax function over the similarity scores of all pairs within the mini-batch, scaled by a temperature parameter

τ

$ℓ (i, j) = - log \frac{exp (Φ (x_{i}, x_{j}) / τ)}{\sum_{k = 1}^{2 K} [1_{[k \neq i]} exp (Φ (x_{i}, x_{k}) / τ)]} .$

(4)

The global loss function is summed across all positive pairs, representing the normalized temperature-scaled cross-entropy loss (NT-XEnt). The numerator $exp (Φ (x_{i}, x_{j}) / τ)$ encourages positive pairs to be closer, while the denominator $\sum_{k = 1}^{2 K} [1_{[k \neq i]} exp (Φ (x_{i}, x_{k}) / τ)]$ introduces competition with all other representations in the batch, treating them as negatives. The contrastive loss can be interpreted as the maximization of the similarity between positive pairs in relation to the similarity between negative pairs. This process effectively forms a distribution over possible pairs, emphasizing the relative similarity of positive pairs over negatives. The temperature parameter $τ$ controls the sharpness of the similarity scores. From a mathematical point of view, this parameter affects the relative weighting of similarities. A lower-value $τ$ leads to sharper distributions, which heavily penalizes dissimilarities between positive pairs, leading to a stronger focus on very close positives. On the other hand, a higher-value $τ$ treats similarities equally, which can lead to the avoidance of overemphasizing the few closest pairs. In general, the temperature term $τ$ can be seen as controlling the entropy of the similarity distribution.

Using the NT-XEnt loss function, the full dictionary is updated using a Stochastic Gradient Descent (SGD) procedure, where the gradient is computed using reverse-mode automatic differentiation. The optimization result leads to more diverse quasi-orthogonal atoms that can better represent all the samples available in the training set. This problem is similar to a frame design problem, in which the atoms are designed to represent the samples better. In the context of SimCDL, we want to randomly initialize a dictionary and optimize it following the SGD procedure. Our experiments demonstrate that relevant results can be obtained for small batch sizes and several iterations, leading to better representation errors. The idea of SimCDL is summarized in Algorithm 1.

The contrastive representation learning optimizes asymptotically two main properties: the alignment of features from positive pairs and uniformity of the induced distribution of the features on the hypersphere. In a theoretical study [12], the authors demonstrated that the NT-Xent loss inherently promotes uniformity on the hypersphere. The property of alignment ensures that a pair of positive samples

(x_{i}, x_{j})

pushes them closer together in the latent space. This can be seen as maximizing the similarity

E [Φ (x_{i}, x_{j})] \to \max

, encouraging the alignment of different augmentations from the same sample. The property of uniformity pushes negative pairs apart. In this way, the representations are spread over the entire space,

E_{k \neq i} [Φ (x_{i}, x_{k})] \to \min

, with the aim of achieving a uniform distribution over the unit hypersphere. These properties share similarities with the concept of the incoherence of atoms in dictionary learning. The underlying goal of the problem is the same, but applied in a different context. In dictionary learning, coherence refers to the similarity between different atoms. This suggests that the use of contrastive representation learning should lead to more incoherent dictionaries. The underlying mechanisms of building incoherent atoms is similar to the strategy of contrastive representation learning. Moreover, contrastive learning is related to maximizing the mutual information (MI) [13] between different augmentations of the same sample:

$MI (\tilde{x_{i 1}}; \tilde{x_{i 2}}) \geq E [log p (x_{i} | x_{j}) - log p (x_{i})],$

(5)

where $\tilde{x_{1}}$ and $\tilde{x_{2}}$ are different augmentations of $x_{i}$ . The maximization of mutual information for the data samples is related to the problem of reducing mutual coherence in the problem of dictionary learning. Since we want to enhance the representation capabilities (mutual information), more diverse atoms are needed, leading to a reduction in mutual coherence.

Algorithm 1 SimCDL: main learning algorithm

Require: batch size K, constant $τ$ , augmentation function T, dictionary $D$ , sparsity constraint s
for sampled minibatch ${y_{k}}_{k = 1}^{K}$ do
for all $k \in 1, \dots, K$ do
draw two augmentation functions $t \sim T$ , $t^{'} \sim T$
# the first augmentation
${\tilde{y}}_{2 k - 1} = t (y_{k})$
$x_{2 k - 1} = OMP ({\tilde{y}}_{2 k - 1}, D, s)$
# the second augmentation
${\tilde{y}}_{2 k} = t^{'} (y_{k})$
$x_{2 k} = OMP ({\tilde{y}}_{2 k}, D, s)$
end for
for all $i \in 1, \dots, 2 K$ and $j \in 1, \dots, 2 K$ do
$Φ (i, j) = x_{i}^{⊤} x_{j} / (∥ x_{i} ∥ ∥ x_{j} ∥)$
end for
compute gradient of $L = \frac{1}{2 K} \sum_{k = 1}^{K} [ℓ (2 k - 1, 2 k) + ℓ (2 k, 2 k - 1)]$ , where ℓ is defined in (4)
update dictionary $D$ using gradient descent
end for
return learned dictionary $D$

The use of SimCDL can be beneficial for the initialization of dictionaries with incoherent atoms or even incoherent sub-dictionaries. In classification problems, with $Y = [Y_{1}, \dots, Y_{c}, \dots, Y_{C}]$ representing a set of feature vectors, we want to learn local dictionaries, $D_{c}$ , for each class. In general, the initialization problem is not addressed; simple methods like random matrices or a random selection of signals are used for initialization; we will tackle the problem using SimCDL. Considering that a class dictionary, $D_{c} \in R^{m \times N_{c}}$ , should achieve good representations for its class, we will further adapt the SimCRL framework for the initialization of dictionaries in classification problems. Since we need C dictionaries, we will further optimize a wide dictionary, $D = [D_{1}, \dots, D_{c}, \dots, D_{C}] \in R^{m \times (C \cdot N)}$ . During optimization, the sparsity constraint s is set to N, which is the number of atoms per class. Since we need N atoms, we want to overspecialize enough atoms for each class.

After training the general dictionary, the problem of atom distribution must be solved; each atom of

D

must be assigned to a class c. For this task, we propose two different approaches. The first one is greedy: we loop over each class and search for the atoms that are most used in the sparse representation of the samples of the current class. Since class dictionaries do not have common atoms, once an atom is assigned to a class, it becomes unavailable for other classes. The second approach is based on the linear sum assignment problem [14]. This algorithm solves an optimization problem where the goal is to assign a set of workers to a set of tasks in a one-to-one manner while minimizing the total cost of the assignment. This scenario is similar to the problem of assigning the atom class with respect to their use. During our experiments, we tested both methods and decided to use the second approach.

Source link

Denis C. Ilie-Ablachim www.mdpi.com

Greenberg News

A Simple Framework for Contrastive Dictionary Learning

1. Introduction

2. Contrastive Dictionary Learning

Greenberg

1. Introduction

2. Contrastive Dictionary Learning

Related Posts

Buildings, Vol. 16, Pages 396: Modular Chain-of-Thought (CoT) for LLM-Based Conceptual Construction Cost Estimation

Sensors, Vol. 26, Pages 638: Multimodal Building Damage Assessment Method Fusing Adaptive Attention Mechanism and State-Space Modeling

Minerals, Vol. 16, Pages 89: Geochemical Framework of Ata&uacute;ro Island (Timor-Leste) in an Arc&ndash;Continent Collision Setting

Greenberg

Minerals, Vol. 16, Pages 89: Geochemical Framework of Ataúro Island (Timor-Leste) in an Arc–Continent Collision Setting