3.2.1. Hypothesis 1 (H₁): Grade 12 National Senior Certificate Mathematics Positively Predicts Student Performance in the Following University Mathematics Courses: MATM1534, MATM1622, and MATM1644

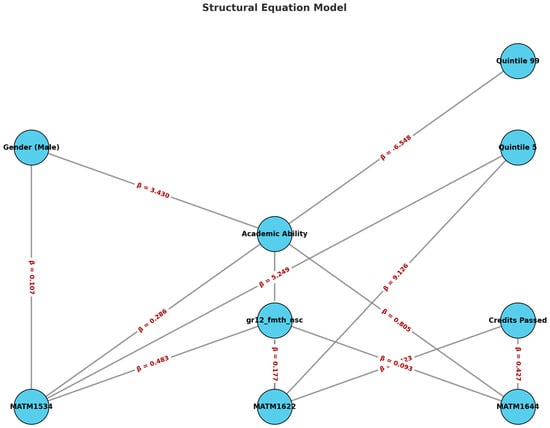
Grade 12 National Senior Certificate Mathematics significantly and positively predicted student performance in MATM1534, β = 0.483, SE = 0.082, z = 5.887, p < 0.001, thereby supporting Hypothesis 1 for this course. In contrast, the predictive effect of Grade 12 National Senior Certificate Mathematics on MATM1622 was non-significant, β = 0.177, SE = 0.181, z = 0.980, p = 0.327, which does not support Hypothesis 1 for this course. Similarly, Grade 12 National Senior Certificate Mathematics did not significantly predict performance in MATM1644, β = 0.093, SE = 0.188, z = 0.495, p = 0.620, failing to support Hypothesis 1 for this course.

Since Academic Ability was measured as National Senior Certificate (NSC) performance in Mathematics and utilised as a latent variable in the structural equation model, these findings suggest that NSC Mathematics performance is a robust indicator of preparedness for MATM1534. This implies that the NSC Mathematics curriculum effectively equips students with the necessary skills and knowledge to excel in MATM1534, whereas its predictive power diminishes for MATM1622 and MATM1644. The differential impact of Academic Ability across these courses may indicate that MATM1534 aligns more closely with the competencies assessed in the NSC Mathematics, highlighting the importance of curriculum alignment in educational preparation and student success.

3.2.2. Hypothesis 2 (H₂): Credits Passed Positively Predict Student Performance in MATM1534, MATM1622, and MATM1644 Courses

Credits Passed was found to significantly and positively predict student performance in MATM1622, β = 0.423, SE = 0.024, z = 17.505, p < 0.001 and MATM1644, β = 0.427, SE = 0.028, z = 15.094, p < 0.001, thereby supporting Hypothesis 2 for these courses. In contrast, the effect of Credits Passed on MATM1534 was non-significant, β = 0.013, SE = 0.010, z = 1.203, p = 0.229, which does not support Hypothesis 2 for this course. Since Credits Passed encompasses the three mathematics modules MATM1534, MATM1622, and MATM1644, as well as additional credits from other courses that students enrol in during their first year, these findings suggest that a higher overall credit accumulation is associated with better performance in the intermediate and advanced mathematics courses MATM1622 and MATM1644. This implies that students who engage in a broader range of coursework and complete more credits are likely to develop a more robust academic foundation, which enhances their ability to excel in these demanding mathematics modules. However, the lack of a significant relationship between Credits Passed and MATM1534 may indicate that this introductory course relies more on specific foundational knowledge and skills directly assessed during the National Senior Certificate (NSC) examinations rather than the cumulative credit load. Alternatively, it could suggest that other factors, such as the introductory nature of the course content or the teaching methodologies employed, influence performance in MATM1534. These differential impacts highlight the importance of considering the diverse academic experiences and course-specific requirements when evaluating the predictors of student success in university mathematics programmes.

3.2.3. Hypothesis 3 (H₃): Gender (Male) Is Associated with Student Performance in the Courses

Gender was examined as a predictor of student performance across three mathematics courses: MATM1534, MATM1622, and MATM1644. In MATM1534, being male was a significant positive predictor of performance, β = 3.197, SE = 1.190, z = 2.686, p = 0.007, thereby supporting Hypothesis 3 for this course. This suggests that male students outperformed their female counterparts in MATM1534. In contrast, the effect of gender on performance in MATM1622 was non-significant, β = −3.294, SE = 2.409, z = -1.367, p = 0.172, which does not support Hypothesis 3 for this course. Similarly, in MATM1644, gender had a negligible and non-significant effect, β = 0.121, SE = 2.691, z = 0.045, p = 0.964, failing to support Hypothesis 3 for this course.

These results indicate that while gender differences in performance are evident in MATM1534, they do not extend to the more advanced courses MATM1622 and MATM1644. The significant gender effect in MATM1534 may reflect differential preparation or engagement levels among male and female students at the introductory level of university mathematics. It is possible that MATM1534, being an introductory course, aligns more closely with the competencies and skills emphasised in earlier educational experiences where gender disparities have been documented. Conversely, the absence of significant gender effects in MATM1622 and MATM1644 suggests that as students progress to more advanced mathematics courses, factors other than gender become more salient in determining academic performance. This could be due to various reasons, including increased self-efficacy, targeted support mechanisms, or the nature of the course content that mitigates initial gender disparities. The findings highlight the importance of addressing gender-specific needs and promoting equitable learning environments, particularly in introductory courses where disparities are more pronounced. Future research should explore the underlying mechanisms contributing to gender differences in initial mathematics performance and investigate strategies to support all students in achieving academic success across all levels of university mathematics courses.

3.2.4. Hypothesis 4 (H₄): Socioeconomic Status (SES), as Indicated by Quintile Placement, Is Associated with Student Performance in the Courses

Quintile placement was examined as a predictor of student performance across three mathematics courses: MATM1534, MATM1622, and MATM1644. In MATM1534, students from the highest SES quintile (Quintile 5) significantly and positively predicted performance, β = 5.249, SE = 1.877, z = 2.796, p = 0.005, thereby supporting Hypothesis 4 for this course. This suggests that students from higher SES backgrounds perform better in MATM1534 than their lower SES counterparts. For MATM1622, both Quintile 5 and Quintile 99 (non-quintile schools) approached significance as positive predictors of performance, β = 9.126, SE = 4.049, z = 2.254, p = 0.024 and β = 10.604, SE = 5.717, z = 1.855, p = 0.064, respectively. While Quintile 5 significantly predicted better performance, Quintile 99 approached significance, partially supporting Hypothesis 4 in this course. This indicates that higher SES continues to be an important factor in predicting student success in MATM1622, and there is a trend suggesting that students from Quintile 99 may also experience enhanced performance. However, this relationship did not reach conventional levels of statistical significance. This makes sense in the context of Quintile 99, which has private schools not classified between 1 and 5 and is also made up of international students.

In MATM1644, Quintile 5 showed a positive trend in predicting performance, β = 6.193, SE = 3.948, z = 1.569, p = 0.117, but this effect was not statistically significant. Additionally, other quintiles did not significantly predict performance in this course, providing limited support for Hypothesis 4 for MATM1644. This suggests that while high SES may confer some advantages, its impact on performance in MATM1644 is not as pronounced as in the other courses studied.

Since SES was measured using school quintile placement, with Quintile 5 representing the highest SES and Quintile 1 representing the lowest SES, these findings highlight the role of socioeconomic factors in academic performance within university mathematics courses. The significant positive prediction of performance by Quintile 5 in MATM1534 and MATM1622 underscores the advantage that higher SES students may have, potentially due to better access to resources, support systems, and preparatory opportunities. The approaching significance of Quintile 99 in MATM1622 suggests that students from this SES background might also benefit in certain contexts, although further research is needed to confirm this trend.

The non-significant findings for MATM1644 indicate that SES may have a diminished impact on performance in more advanced mathematics courses or that other factors become more influential at this level of study. These differential effects across courses emphasise the complexity of SES influences on academic outcomes and suggest that interventions to reduce SES-related disparities may need to be tailored to each course level’s specific demands and contexts. The results support that SES, measured by quintile placement, is an important predictor of student performance in certain university mathematics courses. These findings advocate for continued attention to socioeconomic disparities in higher education and the implementation of strategies to support students from diverse SES backgrounds to achieve academic success across all levels of their studies.

The analysis revealed that both gender and SES significantly predicted Academic Ability. Specifically, being male was a significant positive predictor of Academic Ability (β = 3.430, SE = 0.949, z = 3.615, p < 0.001), while being in Quintile 99, representing the lowest SES quintile, significantly negatively predicted Academic Ability (β = −6.548, SE = 1.828, z = −3.582, p < 0.001). These findings suggest that male students and those from lower SES backgrounds exhibit variations in Academic Ability, potentially reflecting underlying differences in access to educational resources, support systems, or other sociocultural factors that influence academic performance. Furthermore, significant covariances were observed among the residuals of the mathematics courses, indicating that unmeasured factors influence performance across these courses. Specifically, the residuals of MATM1534 and MATM1622 were significantly correlated (r = 0.286, p < 0.001), as were the residuals of MATM1534 and MATM1644 (r = 0.267, p = 0.001) and MATM1622 and MATM1644 (r = 0.805, p < 0.001). These strong correlations suggest that shared unmeasured variables—such as teaching quality, student motivation, or institutional support—may concurrently affect student performance across multiple mathematics courses.

Regarding the explanatory power of the Model, substantial variance was accounted for in the dependent variables. The Model explained 79.9% of the variance in MATM1534, 40.5% in MATM1622, and 43.6% in MATM1644. Additionally, the Model accounted for 89.3% of the variance in Academic Ability and an impressive 99.8% of the variance in Credits Passed. These high levels of explained variance underscore the robustness of the constructs within the Model and highlight the critical role that Academic Ability and Credits Passed play in predicting student performance across different mathematics courses. The comprehensive variance explained also reflects the Model’s effectiveness in capturing the multifaceted factors contributing to academic success in university-level mathematics.

The SEM results provide detailed perspectives on factors influencing student performance across mathematics courses. Academic ability emerged as a significant predictor solely for MATM1534, indicating that inherent academic competencies may play a critical role in this specific course. However, Academic Ability did not predict performance in MATM1622 and MATM1644, suggesting that other factors may be more influential in these contexts. Credits Passed demonstrated a strong positive relationship with performance in MATM1622 and MATM1644, highlighting the importance of prior academic achievements in predicting future course outcomes. The lack of significance in MATM1534 suggests that course-specific factors or other unmeasured variables might mitigate the influence of credits passed in this setting.

Gender exhibited a significant positive effect only in MATM1534, where male students outperformed their female counterparts. This finding aligns with the existing literature that sometimes reports gender-based performance differences. However, the absence of such effects in other courses indicates that gender may interact with course-specific dynamics. SES, particularly in quintile 5, was a significant predictor for MATM1534, and marginally for MATM1622, underscoring the role of SES in academic performance. The negative association between quintile 99 and Academic Ability suggests that students from the lowest SES backgrounds may face challenges that impact their academic competencies.

The significant covariances among course performances imply that underlying, unmeasured factors, such as teaching quality, student motivation, or institutional resources, simultaneously influence multiple course outcomes. This interrelation underscores the complexity of academic performance and the need for comprehensive approaches in educational research and interventions. The Model substantiates the differential impacts of Grade 12 National Senior Certificate Mathematics, Credits Passed, Gender, and SES on student performance across various university mathematics courses. These findings advocate for targeted educational strategies that comprehensively consider individual attributes and contextual factors to enhance student achievement.