A Sub-Channel Spatial Homogeneity-Based Channel Estimation Method for Underwater Optical Densely Arrayed MIMO Systems

1. Introduction

Visible light communication (VLC) technology utilizes light waves within the visible spectrum for data transmission. Characterized by high bandwidth, low interference, and high security, VLC is emerging as a promising solution for a variety of applications, including but not limited to wireless communication, intelligent transportation, indoor positioning, and underwater communication. Especially in underwater communication scenarios, where the bandwidth for acoustic communication is limited and radio frequency communication experiences severe attenuation, VLC has emerged as one of the few viable options for short-range, high-bandwidth communication underwater [1,2]. To enhance the performance of VLC systems, a MIMO [3] structure is typically employed, featuring multiple light sources and photodetectors (PDs), which enrich the optical links and achieve higher diversity and multiplexing gains.

Currently, the modulation bandwidth of conventional photodetectors (PDs), such as avalanche photodiodes, and common light sources, like laser diodes, has long exceeded gigahertz and even reached terahertz. While the modulation bandwidth of a light-emitting diode (LED) is typically constrained by its inherent junction capacitance, those designed for illumination purposes generally achieve only a few megahertz [4]. To broaden the modulation bandwidth of LEDs to hundreds of megahertz or even gigahertz, one could employ pre-equalization technology [5,6] to optimize the power spectrum of the transmitted signal or modify the doping, structure, and materials of the LED itself, such as micro-LED and GaN-LED [7,8]. The deployment of high-speed light sources and PDs significantly elevates the symbol rate up to the Gbaud level for underwater optical communication systems.

In indoor optical communication scenarios, the effects of the air medium are commonly neglected, with the Lambert’s model [9] being utilized for sophisticated modeling. Conversely, in underwater optical communication, the water medium’s absorption, scattering, and refraction have substantial impacts, making the communication model notably more complex. In clear water and coastal regions with high water quality, the medium’s impact can be concisely and efficiently modeled using Beer’s law. Nonetheless, in turbid harbor waters where refraction and scattering are pronounced, the complexity of the optical communication model escalates significantly. Within these challenging environments, channel estimation and signal detection for optical communication systems confront serious challenges. This paper focuses on this scenario, with the goal of boosting the efficiency of channel estimation under these demanding circumstances.

The distribution of the scattering angle is predominantly described by phase functions, such as the Henyey–Greenstein (HG) and the fast Fourier transform (FFT) [10,11]. This scattering effect enriches propagation pathways for photons at the microscopic level, manifesting as a transmission delay of symbols at the macroscopic level. Enhanced communication distances or diminished water quality substantially augment the quantity of serpentine photons, consequently intensifying the observed transmission delay. At elevated symbol rates, the transmission delay can precipitate intersymbol interference, degrading the underwater optical channel into one that exhibits frequency-selective fading. This suggests that the DC gain alone is inadequate to comprehensively characterize the channel attributes in underwater visible light communication MIMO (UVLC-MIMO) systems.

In pursuit of acquiring comprehensive CIR or CFR information, numerous channel estimation methods have been put forward. The LS [12,13] and minimum mean square error (MMSE) [14] methods are popular for linear channel estimation. These methods enable the complete CFR to be obtained through interpolation and are part of the frequency-domain channel estimation strategies. Given the channel length beforehand, the estimates of the LS method can be converted to the time domain via discrete Fourier transform(DFT) for further noise reduction, which is known as the LS-DFT method [15]. However, the demand for pilots in linear channel estimation methods significantly rises with the expansion of MIMO array elements. The non-negative constraint for optical signals complicates the direct application of orthogonal frequency division multiplexing (OFDM) modulation techniques. Two widely used optical OFDM schemes are DC-biased OFDM (DCO-OFDM) [16] and asymmetric clipper optical OFDM (ACO-OFDM) [17]. Both schemes reduce the number of available subcarriers, cutting spectral efficiency and complicating channel estimation strategies. To enhance bandwidth utilization, researchers have superimposed multi-order pulse amplitude modulation (MPAM) streams on ACO-OFDM’s even subcarriers, creating a hybrid OFDM and MPAM structure, and used interference cancellation techniques [18,19] to separate these streams at the receiver. While these strategies partially address the bandwidth limitations of optical OFDM systems, they do not significantly change the incremental ratio of pilots to array elements (IR-PE). In other words, enlarging the array size still depletes the scarce data subcarriers rapidly. Thus, in UVLC-MIMO systems, curtailing the IR-PE is crucial for scaling up optical MIMO arrays.

In light of the time-domain sparsity of optical communication channels, CS-based channel estimation methods can be leveraged to reduce pilot overhead. The goal of CS-based channel estimation methods is to accurately capture the sparse distribution and intensity characteristics of the CIRs. OMP [20] is a classical method for CIR reconstruction in sparse channels, which is known for its straightforward process and effective performance in estimating CIR intensity. However, OMP necessitates prior insight into the sparsity level of the target signal, and its greedy strategy selects only the currently best-matching atom in each iteration, potentially overlooking other effective combinations. This tendency may cause OMP to become trapped in a local optimum. To achieve sparsity adaptation, regularized orthogonal matching pursuit (ROMP) [21], sparsity adaptive matching pursuit (SAMP) [22] and other improved methods for CIR length adaptation have emerged. To ensure that the results of the greedy search are globally optimal, numerous scholars have proposed corresponding backtracking search mechanisms, such as A*OMP [23] and subspace pursuit (SP) [24]. These methods significantly enhance the precision of channel estimation in MIMO systems with small arrays. However, as the size of the MIMO array increases, the number of sub-channels rises exponentially, necessitating a substantial increase in pilot overhead to ensure reconstruction accuracy. To address this issue, numerous researchers have proposed targeted strategies, including structured-compressed sampling matching pursuit (S-CoSaMP) [25] and joint orthogonal matching pursuit (JOMP) [26]. These methods exploit the structural sparsity of the sub-channels in centralized massive MIMO systems to enhance the estimation precision of the CIR distribution. Furthermore, the temporal correlation of the channel is leveraged to transform the reconstructed objectives into CIR variations, which are sparser, reducing the pilot overhead [27,28]. Unfortunately, factors such as water flow disturbances and the unpredictable motion of underwater vehicles introduce random fluctuations in the optical path direction. These fluctuations shorten the channel’s coherence time and diminish the sparsity advantage of CIR variations. Although the CS-based channel estimation methods exhibit a more pronounced suppression on the IR-PE compared to frequency-domain estimation strategies like the LS and MMSE methods, it is crucial to ensure the reconstruction probability of the CIRs by guaranteeing that the number of pilots exceeds twice the column rank of the sensing matrix, adhering to the SPARK criterion [28]. In optical OFDM systems, particularly in ACO-OFDM, the presence of limited pilot resources leads to an excessively high IR-PE, which poses a significant challenge for scaling up the array elements in UVLC-MIMO systems. Referring to the compensation mechanism that relies on CFR interpolation in linear channel estimation methods, it is anticipated that a further reduction in IR-PE will be realized by employing the reconstruction of sparser parameters derived from a prior CIR model rather than directly using CIR sample reconstruction.

To delineate the influence of scattering effects on symbol transmission delay in underwater settings, Tang et al. [29] and Zhang et al. [30], respectively, used a dual Gamma function (DGF) and a weighted dual Gamma function (WDGF) to model the CIR of an underwater optical channel. In [31], the DGF is utilized to model the channels of a relay-assisted optical wireless communication system under turbid water conditions. Subsequently, Li et al. [32] put forth a multi-Gamma function (MGF) to characterize the CIR in the scenario of underwater long-range laser communication, drawing on the two aforementioned models as a foundation. These CIR models, primarily composed of the product of linear and exponential terms, manifest a morphology characterized by enhancement followed by exponential decay at picosecond-level channel sampling intervals. In [33,34], a more complex power-quotient structure function is employed as the coefficient term in the CIR model to enhance the fitting accuracy. With the channel sampling interval extended to the nanosecond scale, the temporal resolution diminishes, consequently leading to the degradation of the CIR model into a simpler, monotonically decaying exponential form. Accordingly, a CIR model-based channel estimation method can be implemented with the goal of achieving a further reduction in the IR-PE.

Beyond the prior CIR model, the spatial correlation of sub-channels [35,36] in UVLC-MIMO systems also plays a pivotal role in further mitigating the IR-PE. Limited by surface area and structural constraints, compact underwater communication devices frequently face restrictions on the arrangement and spacing of array elements within UVLC-MIMO systems. The restricted spacing of array elements enhances the spatial correlation between sub-channels, particularly when employing divergent beams. In such scenarios, the sub-optical paths of UVLC-MIMO systems undergo significant aliasing, introducing considerable spatially correlated interference among the sub-channels. Space–time block coding (STBC) [37] and space–frequency block coding (SFBC) [38] are proven techniques for managing interference arising from spatially correlated sub-channels. These methods yield equivalent channel matrices that are orthogonal or quasi-orthogonal, despite the compromise in communication capacity. In contrast, the high spatial correlation of sub-channels, in turn, facilitates the channel estimation process. Particularly in UODA-MIMO systems, sub-optical paths share the identical water medium and the corresponding sub-channels exhibit SSH characteristics. The SSH in this paper is defined as CIRs or CFRs having identical morphologies but varying amplitudes. This implies that, armed with an a priori CIR model and the SSH characteristic, one needs only to estimate the intensity related to the CIR model, thereby reducing the dimensionality of the estimation target.

The primary objective of this study is to construct more sparse reconstruction targets for UODA-MIMO systems on the basis of CS channel estimation technology, further decrease the lower bound of pilot requirements and consequently diminish the IR-PE. To this end, we ingeniously merge the time-domain sparsity and sub-channel spatial homogeneity inherent to the UODA-MIMO systems, and we put forth a channel estimation method based on CS techniques and a prior CIR model. Within the SPARK criterion, the proposed method achieves a reduced pilot frequency requirement compared to traditional compressive sensing methods, including OMP, SAMP, and S-CoSaMP. The main work of this paper includes the following:

The present study analyzes the CIR characteristics of an LED-based underwater optical communication system at Gbaud symbol rates using Monte Carlo photon tracing simulations. Accordingly, a monotonically decaying exponential CIR model is established, and its effectiveness is subsequently evaluated through experimental analysis.
We pioneer the concept of SSH and subsequently affirm its applicability in UODA-MIMO communication contexts. This is achieved by dissecting the CIR’s morphological traits and the correlation coefficient derived from CIRs in photon tracking simulations.
A channel estimation method for UODA-MIMO systems, grounded in CS techniques and a prior CIR model, is proposed. Its performance is confirmed in an ACO-OFDM-MIMO system characterized by low pilot overhead and SNR.

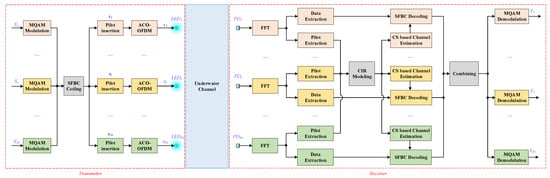
The rest of the paper is organised as follows. The architecture of the UODA-MIMO system, which incorporates the ACO-OFDM modulation scheme, the SFBC and the novel SSH-CE method, is presented in Section 2. Section 3 delves into the photon tracing methodology and the corresponding CIR modeling process. In Section 4, we provide an in-depth discussion on the specific implementation details of the SSH-CE method. Section 5 outlines the experimental setup and presents an exhaustive analysis of the established system along with the proposed SSH-CE method. Lastly, Section 6 offers discussions and a summary of our findings.

Notation: In this paper, $\oplus_{ν = 1}^{N} (\cdot)$ denotes the direct sum of N matrices or vectors. ⊗ is the Kronecker product operation. $\cup_{ν = 1}^{N} (\cdot)$ denotes the equivalent division of a set into N subsets, where ∪ is the union operation. $〈\cdot〉$ stands for the total number of elements contained within a set or table. ${∥\cdot∥}_{2}$ represents the Euclidean norm. $F (\cdot)$ is the DFT, and $F^{Ξ} (\cdot, N)$ denotes the set of N-point DFT results with column index set $Ξ$ . ${(\cdot)}^{T}$ and ${(\cdot)}^{H}$ are transpose and conjugate transpose operations, respectively. $I_{N}$ is an identity matrix of order N.

4. SSH-Based Channel Estimation Method Utilizing Compressive Sensing

The sub-channels of the UODA-MIMO system are highly spatially correlated and tend to be homogeneous; all sub-channels are considered to share an identical CIR model. In the equation discussed, the parameters of linear term in the CIR model differ across sub-channels, while the parameters of the exponential decay terms are uniform.

$\{\begin{matrix} {\overset{⇀}{R}}_{j} & = [C_{1_1 j}, \dots, C_{1_i j}, \dots, C_{1_N_{t} j}] \\ \overset{⇀}{ρ} & = [e^{- C_{1}^{[3]} Δ} + e^{- C_{2}^{[3]} Δ}, \dots, e^{- C_{1}^{[3]} L Δ} + e^{- C_{2}^{[3]} L Δ}] \end{matrix} .$

(16)

In this context,

C_{1_i j}

serves as a shorthand for the linear term parameter

C_{1_i j}^{[1]}

of the

i, j

-th sub-channel CIR.

C_{1}^{[3]}

and

C_{2}^{[3]}

represent the common parameters of exponential decay terms across all sub-channel CIRs. Given the spatial homogeneity of the sub-channels and the uniformity of all exponential decay terms, it becomes feasible to consolidate all sub-channel CIRs and the sensing matrix using the combining law. This approach leads to a significant reduction in sparsity of the reconstructed object from the original

N_{t} K

K

. Consequently, the reconstruction model for the parameters of the common exponential decay term is reformulated as

${\overset{⇀}{Y}}_{j}^{Ω} = {\dot{A}}_{j} {\dot{\overset{⇀}{h}}}_{j} + {\overset{⇀}{Z}}_{j}^{Ω},$

(17)

where ${\dot{A}}_{j} = \frac{1}{N_{t}} \sum_{i = 1}^{N_{t}} A_{i j}$ , $A_{j} = \oplus_{i = 1}^{N_{t}} A_{i j}$ . ${\dot{\overset{⇀}{h}}}_{j} = \frac{1}{N_{t}} \sum_{i = 1}^{N_{t}} {\overset{⇀}{h}}_{i j}$ represents the consolidated CIR of all sub-channels with a single linear term parameter ${\dot{C}}_{1_j} = \frac{1}{N_{t}} \sum_{i = 1}^{N_{t}} C_{1_i j}$ . The consolidated sub-channel CIR is reconstructed using the OMP method, and it is subsequently fitted to the prior CIR model described in Equation (15), thereby yielding

${\hat{\dot{\overset{⇀}{h}}}}_{j} = {\hat{\dot{C}}}_{1_j} \hat{\overset{⇀}{ρ}} .$

(18)

In this context, ${\hat{\dot{C}}}_{1_j}$ signifies the fitted value of the ${\dot{C}}_{1_j}$ . Similarly, $\hat{\overset{⇀}{ρ}}$ denotes the fitted result of $\overset{⇀}{ρ}$ , which is formulated as $\hat{\overset{⇀}{ρ}} = [e^{- {\hat{C}}_{1}^{[3]} Δ} + e^{- {\hat{C}}_{2}^{[3]} Δ}, \dots, e^{- {\hat{C}}_{1}^{[3]} L Δ} + e^{- {\hat{C}}_{2}^{[3]} L Δ}]$ . ${\hat{C}}_{1}^{[3]}$ , ${\hat{C}}_{2}^{[3]}$ are the fitted values of $C_{1}^{[3]}$ , $C_{2}^{[3]}$ . Nevertheless, the linear term parameters of sub-channel CIRs remain unidentified and necessitate further investigation.

The index set

Ω

of pilot subcarriers is divided equally into two sets,

Σ

and

Φ

. The former is employed for reconstructing the linear term parameters of sub-channel CIRs, while the latter is applied for the residual compensation of the sub-channel CIRs. Accordingly, the CS-based channel estimation model for the linear term parameters, as presented in Equation (3), is adjusted to

${\overset{⇀}{Y}}_{j}^{Σ} = {\tilde{A}}_{j} {\overset{⇀}{R}}_{j} + {\overset{⇀}{Z}}_{j}^{Σ} .$

(19)

Here, ${\overset{⇀}{Y}}_{j}^{Σ}$ denotes the received data corresponding to $Σ$ at the j-th PD, while ${\overset{⇀}{Z}}_{j}^{Σ}$ signifies the independently and identically distributed additive Gaussian white noise affecting the same group of subcarriers. ${\tilde{A}}_{j} = A_{j}^{Σ} \hat{γ}$ is the equivalent sensing matrix, $\hat{γ} = \hat{\overset{⇀}{ρ}} \otimes I_{N_{t}}$ , $A_{j}^{Σ} = [S_{1}^{Σ} F_{L}^{Σ}, \dots, S_{i}^{Σ} F_{L}^{Σ}, \dots, S_{N_{t}}^{Σ} F_{L}^{Σ}] \in C^{| Σ | \times N_{t} \cdot L}$ . By utilising the CS-based method, it is possible to ascertain the reconstructed vector ${\hat{\overset{⇀}{R}}}_{j}$ of linear term parameters, ${\hat{\overset{⇀}{R}}}_{j} = {[{\hat{C}}_{1_1 j}, \dots, {\hat{C}}_{1_i j}, \dots, {\hat{C}}_{1_N_{t} j}]}^{T}$ . The sub-channel CIRs are integrally reconstructed through the ${\hat{C}}_{1}^{[3]}$ , ${\hat{C}}_{2}^{[3]}$ and ${\hat{\overset{⇀}{R}}}_{j}$ as

${\hat{\bar{h}}}_{j} = {[{\hat{\overset{⇀}{h}}}_{1 j}, {\hat{\overset{⇀}{h}}}_{i j}, \dots, {\hat{\overset{⇀}{h}}}_{N_{t} j}]}^{T}, {\hat{\overset{⇀}{h}}}_{i j} = {\hat{C}}_{1_i j} [e^{- {\hat{C}}_{1}^{[3]} Δ} + e^{- {\hat{C}}_{2}^{[3]} Δ}, \dots, e^{- {\hat{C}}_{1}^{[3]} L Δ} + e^{- {\hat{C}}_{2}^{[3]} L Δ}] .$

(20)

Considering the observed discrepancy between the reconstructed CIRs from the prior model and the actual sub-channel CIR, a re-estimation procedure is essential to accurately rectify this deviation. By subtracting the reconstructed sub-channel CIRs from the received signal within the CS model, a more sparse representation is attained, namely, the CIR residuals of the sub-channels. By adopting the CIR residual as the focus of CS estimation, the pilot overhead is significantly reduced. Given that the energy in the trailing part of the CIR for short-range underwater optical communication links is inherently minimal and approximates zero, the CIR residuals predominantly concentrate on the first half of the sub-channel CIRs. Consequently, the estimation of CIR residuals is constrained to

[1, K / 2]

. The CIR residual compensation model is formulated as

$Δ {\hat{\overset{⇀}{Y}}}_{j}^{Φ} = A_{j}^{Φ} Δ {\hat{\bar{h}}}_{j} + {\overset{⇀}{Z}}_{j}^{' Φ} .$

(21)

Note that $A_{j}^{Φ} = [S_{1}^{Φ} F_{L}^{Φ}, \dots, S_{i}^{Φ} F_{L}^{Φ}, \dots, S_{N_{t}}^{Φ} F_{L}^{Φ}] \in C^{| Φ | \times N_{t} \cdot L}$ , where $Δ {\hat{\overset{⇀}{Y}}}_{j}^{Φ} = {\overset{⇀}{Y}}_{j}^{Φ} - Δ {\hat{\overset{⇀}{Y}}}_{j}^{Φ}$ and ${\overset{⇀}{Z}}_{j}^{' Φ}$ are representative of the pilot residual and the noise vector associated with $Φ$ received by the j-th PD. $Δ {\hat{\bar{h}}}_{j} = {\bar{h}}_{j} - {\hat{\bar{h}}}_{j}$ signifies the residual between the actual sub-channel CIR and the fitted one. Accordingly, sub-channel CIRs of the UODA-MIMO system with LED beams are constructed as

${\overset{⌢}{\bar{h}}}_{j} = {\hat{\bar{h}}}_{j} + Δ {\hat{\bar{h}}}_{j} .$

(22)

Here, the CIR residuals, denoted as $Δ {\hat{\bar{h}}}_{j}$ , are reconstructed using a matching pursuit method with a sparsity of $K / 2$ . Owing to the independence between the fitting of the exponential decay term and the subsequent linear parameter reconstruction and residual compensation, the pilot frequencies used in these two stages can be shared without incurring additional pilot frequency costs.

Source link

Guojin Peng www.mdpi.com

Greenberg News

A Sub-Channel Spatial Homogeneity-Based Channel Estimation Method for Underwater Optical Densely Arrayed MIMO Systems

1. Introduction

4. SSH-Based Channel Estimation Method Utilizing Compressive Sensing

Greenberg

1. Introduction

4. SSH-Based Channel Estimation Method Utilizing Compressive Sensing

Related Posts

Environmental Factor – September 2023: Summer internship program wraps with research presentation showcase

Characterization, Antimicrobial Potential, Angiogenesis, and In Ovo Safety Profile Assessment

Environmental Factor – September 2023: Diet and exposures in pregnancy: grantee tackles research, messaging

Greenberg