Aircraft System identification provides a platform for the mathematical mapping of a more accurate and robust dynamical model of the aircraft, predicting stability and a control mechanism, and leading to efficient and effective refinement in performance measures. Two approaches are generally adopted for input design; the first is a ‘wide frequency’ range with ‘constant power’ across the complete spectrum; and the second is the input with a specific ‘tailored frequency’ for the aircraft. The broad range includes frequency sweeps and impulse inputs. The second category, input with customized frequency, also referred to as optimal input, is designed as per the dictates of aircraft aerodynamic characteristics, in-line with its natural frequencies. This includes doublets, square waves, and multi-sine inputs [1,2]. In the system identification, an optimal input design remains unique for every set of problems [2], and a customized input for one problem cannot be optimum for any other problem. Our research focuses on discovering a discrete-time, open-loop, longitudinal dynamic model of supersonic aircraft (F-16), using a two-staged optimal input. Therefore, binary periodic inputs with complete control over excitation amplitudes have been chosen [2]. A novel algorithm for multi-stage input optimization has been proposed in this paper, and it demonstrates the stepwise refinement of the input by optimizing PRBS parameters as per aircraft spectral features obtained from the non-parametric model estimation, i.e., FIR, further second stage refinement of frequency, amplitude, order, and periodicity, by maximizing the Fisher Information Matrix by using D-optimality and crest factor.

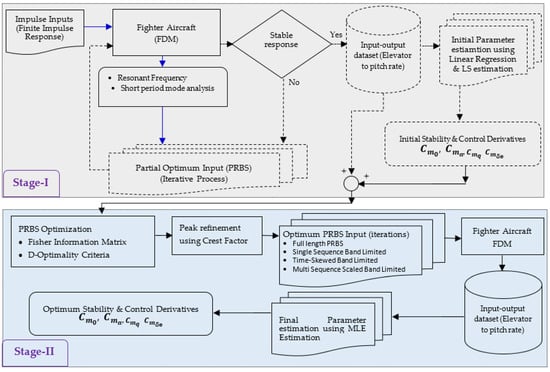
In Figure 1, the research framework is presented in two colored boxes, as follows: Stage-I (gray color) and Stage-II (blue color). Stage-I sets the foundation for partial optimum PRBS input and Stage-II formulates the fully optimum PRBS input. The dashed boxes and arrows represent the initial values, iterations, processes involving the input–output dataset, parameters, and PRBS inputs; whereas the continuous solid lines indicate the final values, iterations, and processes of the same elements. The blue-colored arrows in Stage-I indicate the FIR modelling cycle. The FIR model, by definition, extracts the finite impulse response characteristics (damping rate, input–output delays) of the aircraft dynamical system within a specific time window, as the output becomes zero after a finite duration [2]. The FDM of F-16 aircraft used in this optimization process has been acquired from Stevens et al. [3].

In Stage-I (gray box), the spectral characteristics of the fighter aircraft (F-16) FDM are discovered by using non-parametric modelling (FIR), i.e., natural frequency, desired input pulse-width, and short-period mode analysis (blue arrows). This dynamical behavior, coupled with aircraft constraints, further leads to the design of the initial PRBS input parameters, i.e., frequency ($f_n$), amplitude (U), order (n), and sampling periodicity (Np), through an iterative process. The obtained partial optimum PRBS input is further utilized to excite the aircraft FDM, to acquire the SISO input–output database. Since the research only focuses on longitudinal dynamics, the PRBS input is given as an elevator (δe) input to the FDM, and the output in the form of pitch rate (q) is recorded through successive iterations (necessitating stable response from the FDM). This input–output dataset is used to postulate the initial parameters (stability and control derivatives of longitudinal dynamics, $C_{m_0}, C_{m_{\alpha }}, C_{m_q}, C_{m_{\delta e}}$) by using Linear Regression and LS estimation. The PRBS obtained in Stage-I is considered to be partial optimal, as the constant nature of the PRBS amplitude causes over-parameterization or misspecification of the dynamical model [1]. To tackle this issue, further optimization of the PRBS input parameters is needed, thus leading this research to Stage-II optimization (blue box).