Biological growth has significant hydrodynamic impact on offshore structures, including the new-generation wind turbines which can be very slender. However, ecologically realistic growth models of biological species are often lacking in this regard, leading to inaccuracies around lifetime loads from marine growth. This can be linked to the safety and performance of these structures due to inaccuracies in hydrodynamic loads generated from such growths. While impacts of waves, sea states and wave forecasting have seen extensive research around marine structures and shipping, insights into ecologically consistent marine growth models are significantly less known. Marine growth remains a significant challenge for ocean infrastructure and shipping. In particular, it has been an issue for oil and gas industries as well as renewable energy industries [1,2,3]. Marine growth accumulates on structures causing several undesirable effects such as increased weight, increased drag forces, increased surface area and corrosion of the structure [4,5]. This requires marine growth to be considered when building marine infrastructure with a significant lifetime. The growth must be accounted for either through cleaning or engineering a structure or developing structures or even vessels resilient enough to tolerate these effects [6].

Several weeks after the initial deployment of a structure, marine growth begins to accumulate. This occurs after a biofilm of microorganisms has accumulated on the structure [7]. Consequently, to account properly for marine growth at a site, there is a requirement of modeling such growth with accuracy and detail. Models of marine growth come in a number of approaches. There are individual-based models (IBMs), where the purpose of the growth model is to model individual organisms and their characteristics, as well as population-level models (PLMs), where the purpose is to model the number of members of the population. The purpose of a PLM is often, ultimately, to predict the geometry of the structure’s surface including the accumulated marine growth. For this reason, unlike traditional growth models, the concern is not with the shape nor the number of individuals but rather the accumulated thickness of marine growth when considering lifetime structural effects as a function of such growth.

Some models focus on predicting individual characteristics of the marine organisms such as shell length using environmental factors such as chlorophyll-a concentration or temperature [8]. Other models include those that use historical measurements of marine growth and often statistically predict the extent of marine growth [9,10].

In recent years, efforts have been made to combine these two approaches to create statistically informed models of growth which use environmental parameters to predict growth [11]. There have also been models of biological growth which have global applications [12]. The model outlined in this paper attempts to unite some of the most important and useful features of each of these approaches, creating a statistically and biologically informed globally applicable model for marine growth. The model thus assimilates key biological aspects at a species level into a single model, including environmental factors. This leads to a realistic, biologically consistent growth model with an element of stochastic randomness. The model also allows for site-specific assessments and the possibility of expanding as new geophysical, biological, environmental or ecological information come in.

The blue mussel (Mythulis Edulis) is chosen as the model organism for growth in this model for a number of reasons. First, Mythulis Edulis is the most prevalent organism in terms of biomass that appears on marine structures in the location chosen. Secondly, Mythulis Edulis is also used in aquaculture, and as such, there is extensive research surrounding the organism’s growth. Finally, Mythulis Edulis is a hard-bodied organism, which not only leads to significant hydrodynamic effects but also lends itself for an easier integration of the external thickness of the structure. This is in contrast to soft-bodied growths such as seaweed, which would deform in the flow surrounding a cylindrical structure, resulting in difficulties and uncertainties in terms of defining the surface for the structure [13]. Hard-bodied marine growth can be directly treated as a change in the geometry of the structure, but a biologically or ecologically unaware creation of such geometry would lead to inaccuracies of such growth, and consequently, the impact of such growth on the structure over its lifetime will not represent real-world conditions. While it is possible for hard-bodied growth to move over time to some extent, the growth is considered here as a solid medium. The paper also considers the hard growth to be non-porous, where the opening and closing of the bivalve as well as the fluid contained within the shell of the bivalve are not considered.

Modelling marine growth in a reasonably realistic manner can often be an extremely difficult task, since there are a number of unpredictable elements in the system. For example, there are individual genetic differences between specimens of the same species affecting the rate at which they grow [14]. There are interactions between organisms of different species where predation and parasitism can kill the organism or affect its growth. There are responses to external factors such as temperature [15,16] and salinity [17,18], which change the rate of growth of an organism as well as many others. This paper uses fundamental mathematical principles to account for these factors and creates a biologically informed model of growth rather than the approach of fitting expected growth to statistical representations of marine growths [9,19].

The model proposed in this paper provides a prediction for the bulk thickness of hard marine growth at a given location. The key equation behind this model that describes the change in thickness is based on three fundamental behaviours of the hard organism, which is modelled here focusing on the blue mussels species These behaviours lead to growth through feeding on nutrients in the water column, death by competition or other factors, and movement from areas of low survivability to those of higher survivability. The mussels grow by feeding on chlorophyll-a located in the water column, and they also die due to competition. This model does not account for predation from organisms such as starfish or through detachment due to storms. It is possible to include this, but compared to the mussel death, the impact is usually significantly lower. Finally, in this model, the mussels move to avoid competition if there is a more hospitable environment close by. This is also an important aspect in terms of their growth in realistic conditions. The model can be expressed as

where $Th(t,z)$ is the thickness of growth at a given location and time, $p(t,z)$ describes the distribution of the external factors that affect growth with space and time, i.e., temperature and chlorophyll-a concentration, $\eta$ describes the death coefficient, and $\nu$ describes the diffusion coefficient (rate of movement of mussels). Finally, $DB\left(z\right)$ refers to the Brownian increment which is applied at each location independently in the model. This Brownian increment is comprised of a constant portion and a normally distributed portion. These are typical processes used in an attempt to capture the individual variance that is seen within the mussels or other hard growth as well as the non-uniform attachment of growth to the structure [10,20]. This helps to give rise to the peaks and troughs associated with realistic marine growth rather than an unrealistically smoothed growth.

The shape of Equation (1) is associated with three effects: (i) a feeding term (the first term), (ii) a crowding or competition term (the second term), and (iii) a diffusion term (the third term). The rate of thickness of growth is proportionate to the growth itself modified by external factors changing over depth and time, expressed as $p(t,z)$ The crowding term relies on the thickness $Th(t,z)$ and helps limit the upper limit possible based on available nutrient and temperature. The third term is a diffusion term representing the thickness of marine growth on the structure, which has the tendency to spread out along the structure rather than clump together. It should be noted that this effect is weaker when compared to the first two terms.

Equation (1) is not a growth model in itself but instead a model of growth propagation and therefore cannot initiate growth. This is remedied by implementing moments of settlement of mussel larvae that are present in the water column. This settlement occurs at certain periods of the year. The distribution of settlement times is described in detail in [11]. The settlements of mussel larvae on the structure occur at three randomly selected periods. These periods are randomly selected based on known distributions of mussel larva dispersal. Once the larva is settled, it grows at a constant rate for a period of 10 days. After this, the extent of the growth is propagated forward.

The first term of Equation (1) deals with the response of the mussels to the external environment, and much of the biological compatibility in the model is captured within the term $p(t,z)$:

where A is a factor used to scale the growth factors to the actual growth. $\Phi (t,z)$ dictates the response of the mussel to temperature, and $Chl(t,z)$ represents the amount of chlorophyll-a present, which is used as a measure of food present in the water column for the mussels. Change in salinity usually does not change rapidly in marine environments in the time scale considered here, and consequently, the dependence of the response of Mythulis Edulis (blue mussels) to salinity can be ignored here. If the marine environment has consistently low salinity or rapidly changing salinity (e.g., the Baltic sea), salinity will have to be considered [17,18].

The response of growth to temperature is important as the rates of development of mussels and other marine organisms depend strongly on temperature. A growth response curve for temperature is used for this purpose:

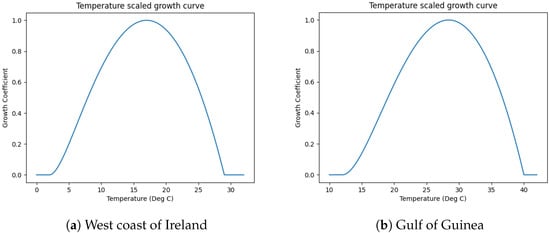
where $\Phi (t,z)$ is the growth factor, $T(t,z)$ is the temperature at a given depth and time, $T_H$ is the upper temperature tolerance of the mussels, and $T_L$ is the lower temperature tolerance of the mussels. The temperature growth curve created from Equation (3) and shown in Figure 1a has an optimal temperature $T_0$ for growth at 17 °C [15,16]. Above and below this temperature, growth is slower. The temperature being above (respectively, below) the upper (respectively, lower) temperature tolerance will result in a null growth factor. This growth coefficient curve can be seen in Figure 1.

Adapting this growth coefficient curve is one of the main components that needs to be adapted to the location of interest as it is indicative of the primary organism’s response to temperature. An inspection of Figure 1 shows that marine growth would not be present in equatorial waters which regularly have temperatures exceeding 30 °C. However, a different growth simulation using data obtained for the Gulf of Guinea demonstrates that to adapt the model to site-specific characteristics, the growth coefficient curve is required to be shifted so that the optimal temperature can be the mean surface temperature. This also allows for ease of handling site-specific information by being able to map them simply in terms of shifts of shapes of curves specific to a species.

Creating a growth profile requires a knowledge of the distribution of the temperature and chlorophyll-a profiles in the area and the distribution with depth. This can be accomplished using a combination of surface measurements of chlorophyll-a and temperature with assumed distribution profiles with depth. The vertical profile of normalised chlorophyll-a is given by

where $C_b$ is the normalised concentration at the surface, s is the normalised slope, $C_{max}$ is the normalised maximum concentration, $z_{max}$ (m) is the depth at which the maximum concentration can be found and $\Delta z$ is the width of the peak. $\overline{ChlA{Z}_{eu}}$ is the average chlorophyll-a concentration of the vertical profile (mg 3⁻³) [21]. Examples are shown in Figure 2.

The vertical distribution of temperature is described as [12]

$T_{surf}$ is the surface temperature of the water, $T_{bot}$ is the water temperature at the sea bottom, and $z_c$ is the depth of the thermocline, while p defines the steepness of the thermocline. The thermocline shape is defined based on the location of the site under consideration. The location is used to decide $T_{bot}$ and p, an example of which is shown in Figure 3.

Once the growth is generated, it can be used for several applications, including engineering information of the hydrodynamics effects of such growth through the use of computational fluid dynamics (CFD) simulations, since they are linked to both the thickness and the surface roughness profiles of the growth [2,22].

The application of the developed model is demonstrated for two significantly different locations globally. We use latitude and longitude (53,$-10$) corresponding to the sea off the west coast of Ireland along with temperature and chlorophyll-a data for this location taken from the European Copernicus satellite. Any location on earth can be considered using the Copernicus satellite to provide a realistic input. Growth is generated subsequently using the approach proposed in this paper over a five-year period deposited on a cylinder of 50 m length and a depth of 2 m. The brownian increment was calculated using $DB\left(Z\right)=0.7+0.6N(0,1)$, where $N(0,1)$ is a normally distributed sample and each Brownian increment is generated independently for each spatial step. Another growth prediction is demonstrated for a more tropical climate using using latitude and longitude of (3.6,8) corresponding to the Gulf of Guinea. This gives a different environment of growth, and this growth is subsequently compared to real-world measurements obtained from previous marine campaigns in that location [19]. For both sites, all coefficients used in the growth model are generated on a trial and error basis, as a small change in growth parameters can have a drastic impact on the overall shape and extent of growth.

An example of these satellite data for a one-year period from 1 January 2017 to 1 January 2018 can be seen in Figure 4 and Figure 5 for chlorophyll-a and temperature, respectively.

These satellite data are subsequently combined with the marine growth model to generate thickness with time steps of 24 h. This time step is sufficient to capture the evolution of parameters in the model and aligned to the time scale of propagation of such changes in real scenarios, such as those considered in this paper. Growth is then propagated over a five-year period. The model is then qualitatively matched against and quantitatively calibrated to campaigns carried out in areas of similar nature. For example, experimental campaigns in the Gulf of Guinea measured hard marine growth up to ten years (e.g., oysters) down to a depth of 40 m. The mean thickness after fourteen years was 102 mm, but the variation over time and growth patterns from the site and fitted straight line models in such measurements demonstrated how over time, these predicted growths changed. This growth is in line with our estimates over five years. For the example of the West Coast of Ireland, a preliminary assessment of metocean site conditions indicates how the marine growth thickness after a few years comes to 50 mm with some variations, which is also what we observe. While a campaign for Ireland was not complete, there are data from a campaign off the coast of Nantes for a similar environment where measurements were carried out from June 2017. Between 10 and 20 m depth, a reference value of growth observed typically was 35 mm. A similar order of magnitude is seen in the simulations, and this was different from the growth and lack of seasonal fluctuations typifying the Gulf of Guinea location. The predictions from the model are then validated for the parameters $\eta$, $\nu$ and A against real data taken from a number of sources [10,19,23]. The values used can be found in Table 1. With data from other locations, this model can be easily calibrated to work for a variety of locations, eventually leading to a global calibration. While databases of extensive marine growth data are not common, the model and the examples presented are expected to provide a compelling case for such a database to be expanded and maintained in the future, engaging several groups globally. While values generated for the location are compared to real-world data, the objective is to match the extent and growth shape rather than to narrow down exact coefficients for the growth model, as there are not enough data sources for this purpose. Often, we are working with only a handful of datasets.

The growth obtained from the application of the proposed model for the west coast of Ireland and the Gulf of Guinea is seen in Figure 6a,b and Figure 7a,b for a discretization of depth in cm. For the west coast of Ireland, a total of five jumps in the thickness of growth are observed corresponding to favourable conditions for the marine life, typically in spring and early summer in the Irish sea. These jumps are almost non-existent for the Gulf of Guinea, which corresponds to the general lack of distinct seasons in that environment. This can be seen in the relatively small variation in the sea surface temperature. It is also important to note that even for similar growth profiles in terms of diameter change, the times of such growths and the rates of change can be very different, thereby leading to substantially varied estimates of stress histograms and also long-term stress fluctuations in a realistic way, which can impact the fatigue performance of these structures as well. The model allows for integrating slower time scale growth models with often commercially available faster time scale models on hydrodynamic effects while also linking to extremely slow lifetime evolution models of safety. Consequently, the use and flexibility of the proposed model for a wide range of applications in a universal sense are possible.

A comparison between Figure 6b and [19] shows how one realisation of a random marine growth model such as the one proposed can capture an example profile of marine growth similar to those obtained in [19]. However, it is important to note that due to this model having random inputs and due to the nature of marine growth itself, this is one realisation of a process that has a huge range of variation, which can be seen in the gathered marine growth data.