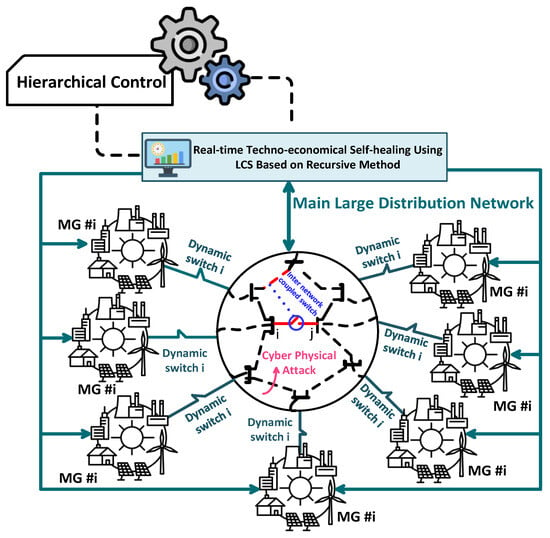
The proposed framework showcases significant robustness in handling various challenges in power management systems, including communication failures, unpredictable power generation, demand uncertainties, and cyber–physical attacks.
5.3.4. Post-Attack Recovery and System Restoration
Resilient Restoration Protocols: Predefined protocols enable the quick restoration of critical infrastructure while gradually re-establishing the less critical parts of the system.
Coordination Between MGs: Interconnected MGs can provide support and flexibility during disruptions, ensuring network stability.
The final and best solutions are summarized as follows.
Figure 14,
Figure 15 and
Figure 16 display the best power generation profiles for each DG during the fluctuations of load in the IEEE 118-, 69-, and 33-bus systems, respectively. These visual representations give great perspectives into the efficient power generation management and the optimization of power flow enabled by optimal dynamic switching under different load conditions.
Furthermore, the PM outlines the optimal arrangements of dynamic switches for the specified line outages across various case studies.
Figure 17,
Figure 18 and
Figure 19 depict the array of the conditions of interconnected switch breakers, aiming to determine the highest effective setup for the initial distribution networks of IEEE 118, 69, and 33, respectively. These visual representations facilitate the identification of the configuration that enhances the performance and efficiency of the network to its fullest extent.
Additionally,
Table 6,
Table 7 and
Table 8 have been painstakingly crafted to present a thorough examination of the performance of the PM in comparison to existing methods. This comparative analysis encompasses a range of vital metrics including economic feasibility, enhancements in the quality of power, improvements in reliability, and considerations for security of network. These tables offer a comprehensive assessment of the optimal techno-economic response to Cyber–Physical attacks across the study period in the IEEE 118-, 69-, and 33-bus networks, offering valuable perspectives into the implications and advantages of the PM.
In the subsequent analysis, the PM is subjected to a fair and equitable comparison with other contemporary approaches. The outcomes of this comparative evaluation are meticulously documented in
Table 6,
Table 7 and
Table 8. Notably, the PM demonstrates its prowess by encompassing all economic and technical objectives within the total objective function during optimization. This achievement is facilitated by our innovative utilization of LCS analysis, allowing for optimization to occur nearly in real-time. Impressively, even for expansive networks like the 118-bus system, optimization completes in less than 2 s, with smaller networks of 33 and 69 buses requiring less than 1 s. Furthermore, the PM adeptly discerns optimal values for independent system parameters, such as optimal generation levels and the configuration of dynamic switches, as evidenced in
Figure 14,
Figure 15,
Figure 16,
Figure 17,
Figure 18 and
Figure 19. In stark contrast, alternative modern methods often grapple with prolonged optimization times, rendering their responsiveness inadequate for immediate decision-making. Conversely, upon scrutinizing various technical and economic objective functions in
Table 6,
Table 7 and
Table 8, it proves that the PM consistently yields the best performance compared to its contemporaries. Subsequently, through a comprehensive assessment of the simulation results depicted in
Figure 14,
Figure 15,
Figure 16,
Figure 17,
Figure 18 and
Figure 19, alongside the data presented in
Table 6,
Table 7 and
Table 8, a nuanced analysis emerges, shedding further light on the efficacy and superiority of the PM. Also, analyzing the outcomes from the simulations of the IEEE 33-, 69-, and 118-bus test systems, as presented in
Table 6,
Table 7 and
Table 8, highlight the clear advantage of the PM compared to existing methods in economic and technical network metrics. This accomplishment is especially noteworthy considering the previous neglect of reliability and power quality indexes in past research. The new methodology effectively enhances DG control within the distribution network and smart MGs by strategically managing power flow dispatch along power network lines and altering energy pathways through dynamic switching within the system.
According to
Table 6, the PM method for the SCL (pu), with a value of 1.93, shows a 54.59% improvement compared to [
33,
34] with a value of 4.25. Compared to [
35,
36], with a value of 6.54, the improvement is 70.49%, and compared to [
37,
38], with a value of 12.37, an improvement of 84.40% is observed. The PM method for VSI (pu), with a value of 9.982, shows a reduction of 46.67% compared to [
33,
34] with a value of 5.32. Similarly, compared to [
35,
36], with a value of 4.28, it shows a reduction of 57.10%, and compared to [
37,
38], with a value of 7.81, it shows an improvement of 21.78%. The PM method for EENS (kWh), with a value of 62.62, shows a 45.18% improvement compared to [
33,
34] with a value of 114.21. In comparison with [
35,
36], with a value of 87.64, the improvement is 28.57%, and compared to [
37,
38], with a value of 314.21, the improvement is 80.06%. The PM method for VD (pu), with a value of 1.36, shows a 79.98% improvement compared to [
33,
34] with a value of 6.791. Compared to [
35,
36], with a value of 5.217, the improvement is 73.94%, and compared to [
37,
38], with a value of 1.87, the improvement is 27.27%. The PM method for Losses (kW), with a value of 1.33, shows a 79.91% improvement compared to [
33,
34] with a value of 6.62. Additionally, compared to [
35,
36], with a value of 8.274, the improvement is 83.92%, and compared to [
37,
38], with a value of 11.427, the improvement is 88.36%. The PM method for Generation Cost (
$), with a value of
$12,687.72, shows a 31.23% improvement compared to [
33,
34] with a value of
$18,452.63. In comparison with [
35,
36], with a value of
$24,384.21, the improvement is 47.95%, and compared to [
37,
38], with a value of
$21,628.64, the improvement is 41.35%. Finally, the PM method for CPU Time for Optimization (s), with a value of 1.12 s, shows a 99.98% improvement compared to [
33,
34], with a value of 6541.2 s. Similarly, compared to [
35,
36], with a value of 8419.1 s, the improvement is 99.99%, and compared to [
37,
38], with a value of 4853.2 s, the improvement is 99.98%. Overall, the PM method significantly improves over the other methods in most metrics.
According to
Table 7, the PM method demonstrates significant improvements across multiple metrics when compared to other methods. For SCL (pu), with a value of 0.751, it shows a 91.18% improvement compared to [
33,
34], which has a value of 8.51, a 92.66% improvement compared to [
35,
36], with a value of 10.24, and a 93.58% improvement compared to [
37,
38], with a value of 11.71. Regarding VSI (pu), the PM method, with a value of 5.00, shows a reduction of 18.76% compared to [
33,
34], a 75.20% reduction compared to [
35,
36], and a 41.16% reduction compared to [
37,
38]. For EENS (kWh), the PM method, with a value of 31.19, shows a 54.27% improvement compared to [
33,
34], a 19.06% improvement compared to [
35,
36], and a 35.76% improvement compared to [
37,
38]. Similarly, for VD (pu), the PM method, with a value of 0.81, shows a 65.53% improvement compared to [
33,
34], an 87.16% improvement compared to [
35,
36], and a 79.64% improvement compared to [
37,
38]. In terms of Losses (kW), the PM method, with a value of 15.09, shows a 28.55% improvement compared to [
33,
34], a 7.53% improvement compared to [
35,
36], and a 17.34% improvement compared to [
37,
38]. For Generation Cost (
$), the PM method, with a value of
$1153.01, demonstrates a 20.66% improvement compared to [
33,
34], a 32.67% improvement compared to [
35,
36], and a 21.64% improvement compared to [
37,
38]. Lastly, for CPU Time for Optimization (s), the PM method, with a value of 0.92 s, shows a 99.98% improvement compared to [
33,
34], a 99.99% improvement compared to [
35,
36], and a 99.98% improvement compared to [
37,
38]. Overall, the PM method consistently shows significant improvements across most metrics when compared to other methods.
As illustrated by
Table 8, the PM method demonstrates notable improvements compared to the other methods ([
33,
34,
35,
36,
37,
38]) across various metrics. For SCL (pu), the PM method, with a value of 0.929, shows a 25.16% improvement over [
33,
34], an 82.41% improvement over [
35,
36], and a 74.69% improvement over [
37,
38]. In terms of VSI (pu), the PM method has a value of 1.55, marking a 25.99% increase compared to [
33,
34], a 127.94% increase compared to [
35,
36], and a 64.89% increase compared to [
37,
38]. For EENS (kWh), the PM method, with a value of 56.08, shows an 11.29% improvement over [
33,
34], a 5.45% improvement over [
35,
36], and a 21.27% improvement over [
37,
38].
When it comes to VD (pu), the PM method, with a value of 0.29, demonstrates an 88.59% improvement over [
33,
34], a 92.43% improvement over [
35,
36], and a 64.20% improvement over [
37,
38]. In terms of Losses (kW), the PM method, with a value of 1.82, shows a 43.30% improvement compared to [
33,
34], a 60.53% improvement over [
35,
36], and a 77.91% improvement over [
37,
38]. For Generation Cost (
$), the PM method, with a value of
$3401.21, provides a 32.82% improvement over [
33,
34], a 27.87% improvement over [
35,
36], and a 28.88% improvement over [
37,
38]. Finally, for CPU Time for Optimization (s), the PM method, with a value of 0.81 s, shows an astounding 99.98% improvement compared to [
33,
34], a 99.98% improvement over [
35,
36], and a 99.97% improvement over [
37,
38].
Overall, the PM method showcases significant advancements across most metrics, especially in terms of CPU Time For Optimization, where it vastly outperforms the other methods by a large margin.