Battery Housing for Electric Vehicles, a Durability Assessment Review

1. Introduction

Mobility has been used to improve societal development due to the feasibility of moving across medium and long distances. However, at the same time, the majority of propulsion systems are fuelled by fossil energy sources, generating a worldwide impact from the pollution generated by internal combustion engines. Approximately 30% of the pollution generated by vehicle emissions occurs in the United States [1]. Moreover, nearly 25% of greenhouse emissions occur in Europe [2]. To reduce these emissions, alternative powertrain systems have been proposed to reduce the emissions from tank to wheel to zero. Regulations are defined for new vehicles regarding CO₂ emissions. The Environmental Protection Agency (

E P A

) defines 82.5 g/km for passenger vehicles manufactured before 2026, while in the European Union the limit is 95 g/km until 2025; this limit is expected to decrease by 30% in 2030 and become zero in 2035 [3,4].

To improve vehicle performance, an electric motor can be added to a vehicle, or the internal combustion engine (

I C E

) can be substituted by an electric motor. These vehicles can be classified based on the hybridization level: microhybrid or start/stop, mild hybrid, full hybrid, plug-in hybrid, and electric [5,6,7,8].

Hybrid electric vehicles (

H E V s

) do not reduce hydrocarbon emissions and can even increase carbon monoxide emissions. This occurs because frequent engine stops and restarts prevent the complete combustion of carbon fuels. Consequently, the catalyst cannot maintain a constant temperature, impairing its ability to function correctly and release combustion gases efficiently. To address these issues, fully electric vehicles are considered the best option for minimizing emissions from tank to wheel. Although electric vehicles themselves do not emit pollutants, the electricity generation process can result in significant emissions. Thus, the environmental benefits of electric cars may be limited unless cleaner energy sources are adopted [9].

The powertrain must overcome inertia loads, such as losses from the engine to the wheel. The energy supplied by the

I C E

is transmitted to the wheels; this transmission process from the engine through the powertrain components has its own losses and depends on its efficiency as well as vehicle requirements and power demand. It depends not only on the internal efficiency of the powertrain components but also on the road conditions (slope, type of road) and the temporal characteristics of the vehicle, such as the passenger number, cargo, rolling resistance, fuel characteristics, drag coefficient, and residual brake [10]. To reduce these losses, powertrain configurations have improved based on vehicle packing. 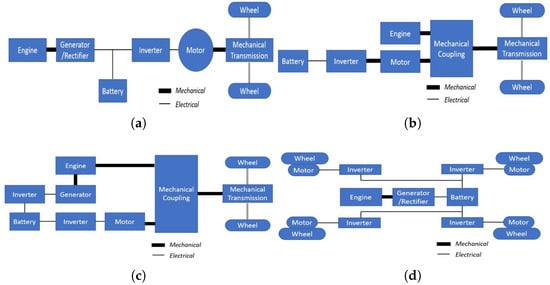Figure 1 shows different architectures for HEVs: series (Figure 1a), parallel (Figure 1b), hybrid (Figure 1c), and all-wheel drive (Figure 1d) architectures.

Batteries generate energy through a chemical process and are used in devices ranging from cell phones and e-bikes to cargo vehicles. However, one of the biggest challenges in transitioning from fossil fuel vehicles to battery-powered ones is the additional weight. This issue is particularly significant for unmanned aerial vehicles, where the battery can account for 20–40% of the total weight [11,12]. However, electric vehicles can reduce emissions by 84% compared with internal combustion engine emissions [1]. The use of lightweight materials increases vehicle autonomy through weight reduction [13], and the battery pack is an essential component of the battery system and contributes to improving vehicle performance and autonomy. Initially, vehicle performance was enhanced by a chemical approach that modified the energy density used in the chemical reactions. Some rechargeable technologies for batteries include magnesium ions, hydrogen, and the most commonly used lithium ions [10,14,15,16]. The other way to improve vehicle performance is to reduce the weight of the battery pack while fixing the chemical process [17,18].

Temperature is an important factor in battery operation due to its effect on efficiency and correct operation; by nature, heat is generated during the chemical process to obtain energy, and it has an optimal range of 15–50 °C and a difference below 5 °C between cells. To reach these limits, thermal management systems (BTMSs) are particularly important and include liquid cooling, air cooling, and phase change materials (PCMs). During the charging and discharging of batteries, a chemical process is generated that generates heat. Keeping the system within an optimal temperature range prevents battery discharge and aging, as well as avoiding operating risks due to overheating. For this purpose, the thermal management system is used to control and dissipate heat through convection, radiation, and conduction. Duct arrangements can be used to work by exchanging heat, using materials such as PCMs [19,20,21,22]. PCMs contribute to heat dissipation and battery cooling. During the transient phase change process, a cooling effect is generated through the PCMs absorbing and dissipating heat [23,24,25,26,27,28,29].

The use of lightweight materials is an essential part of the mobility industry to reduce the impact of the carbon footprint during vehicle operation. While there are areas of opportunity in certain regions for clean energy generation, tank-to-wheel emissions are reduced or eliminated. An essential element for the migration and implementation of hybrid and electric vehicles is the battery, which uses a housing that protects it from impacts, electromagnetic fields, water absorption, and mechanical loads. The reduction of the housing weight contributes to the autonomy of the vehicle. Although the response has been analyzed in vibrations, low impact, and thermal loads, no work has been done to review the fatigue life in composite materials. This work reviews the main load cases, the materials, and analysis methods that allow the evaluation of the durability of the battery housings. Section 2 reviews aspects related to the battery housing, describes its functions, and summarizes the main materials used for its manufacture. Section 3 describes the process of analysis of fatigue in composite materials, for which the main characteristics of load signals, counting processes, as well as damage models for predicting and determining fatigue useful life are described. Section 4 focuses on the use of artificial intelligence for fatigue life prediction. The architecture and definition of characteristics of the neural network to predict durability depend on the characteristics of the damage process; to understand it, the structure of the networks as well as the different types of neural networks are described.

N A R X

dynamic networks are included, which can be used to predict the response as a function of time as in the case of variable amplitude load histories.

3. Fatigue in Composites

Fiber-reinforced composites are the result of the combination of materials applied in different industries, such as the aerospace, automotive, and marine industries. They have the advantages of combining the advantages of each material, as well as improving the mechanical properties of impact, buckling, fatigue, and vibration [55]. The reinforcement can be random (chopped) or through short or long fibers (Figure 2). Depending on the reinforcement definition, which affects the mechanical properties, fiber alignment can increase the tensile strength [56].

Fatigue failure is an accumulated process developed by a cyclic load, and most failures are caused by damage to the component on the matrix, on the reinforcement or in its cohesive area, resulting in a process known as delamination [57,58,59]. In composite materials, fatigue life assessment models can be categorized into property degradation models, progressive damage models, and S–N curve models [60]. Failure is the component response change resulting from fiber fracture, matrix cracking, delamination, or a combination of failure mechanisms [61,62]. Fatigue assessment is complex because it must consider not only the loads, design, materials, and manufacturing processes, but also the changes in all of these processes that modify the linked parameters (materials, loads, design, and manufacturing process) must be considered, as shown in Figure 3. The manufacturing process generates a series of changes that may eventually have an effect on the mechanical performance of various components. The same component design is based on a tolerance according to its operating characteristics and the interaction with other components. Even with the same supplier, materials have small variations in their properties. These variations are included as sources of variability. The source that has the greatest amount of dispersion is the load because the same component with different users generates a different response. In the case of vehicles, aggressive and conservative driving profiles exist. There are maneuvers or road conditions that could generate unexpected loads within the operation of the same vehicle or are defined as abuse when loading the vehicle to the limit, e.g., driving into a pothole. Crossing an irregular road at high speed or encountering a roadblock could also affect the load. This not only generates an additional load but also a possible permanent deformation that modifies the properties of the component.

Material performance depends not only on the constituent materials but also on the reinforcement type (natural or synthetic fibers) and lay-up sequence [63]. The manufacturing process is affected by residual stresses, and, because it can control the fiber orientation distribution through the flow of material inside the mould, the movement depends on the availability of mix movement due to changes in the mould boundaries. The process parameters modify the cohesion that develops between the matrix and the reinforcing fibers due to the combinations of speed, temperature, and time that are generated in the processes between the material and the final component. Figure 4 shows the manufacturing process for the composites. When the reinforcement is generated by dispersed fibers, the manufacturing process does not have much effect; however, when short or long fibers are used, the process has an effect because the same characteristics modify the flow of the fibers in the matrix, either by injection or compression moulding.

There are two ways to analyze a load time history: the time domain and the frequency domain. Figure 5 shows both domains for the same time history. Durability assessment can be performed on both domains, and the time domain can be used to reproduce the multiaxial state of loads or to apply a critical load, e.g., at maximum displacement, considering the degrees of freedom of all the loads. The frequency domain is used for the accelerated fatigue test using the power spectral density (energy at different frequencies). In both cases, environmental conditions can be reproduced to improve the fatigue life prediction [38].

The loads generate a time history that must be analyzed to understand the statistics. The main effect is the number of repetitions to which a load is subjected at a certain amplitude. However, there are low amplitudes that are omitted because, by themselves, they do not cause damage, but when applied to a component that has previous damage they can help propagate the fault. The shape of the load and the velocity at which it is applied are analyzed through the waveform and the frequency of the load. Figure 6 shows a schematic waveform. The waveform statistical characteristics are defined by the stress amplitude (

S_{a}

). The total range from the minimum load (

S_{m i n}

) to the maximum load (

S_{m a x}

) per cycle is expressed as

S_{R}

$S_{R} = S_{m a x} - S_{m i n}$

(1)

$S_{a} = \frac{S_{R}}{2} = \frac{S_{m a x} - S_{m i n}}{2}$

(2)

The mean stress (S_m) is expressed by the mean value of the maximum and minimum loads:

$S_{m} = \frac{S_{m a x} + S_{m i n}}{2}$

(3)

The fatigue damage process is modified by the mean stress and the different relationships that have different loads. It is defined as the ratio of the minimum to maximum stress

(R = S_{m i n} ⁄ S_{m a x})

. When

R \geq 0

, the loads open microcracks, accelerating their propagation, while, when

R = \infty

R > 1

, the load relationships tend to compress and close microcracks, which is beneficial for mechanical fatigue. Figure 7 shows different stress ratios.

The cyclic strength is expressed by comparing the amplitudes of the loads (S) and their expected life (N) for the ith load level. The S–N curve cannot be used to generalize the dynamic strength per se. It is necessary to consider factors (C) such as the type of load, surface roughness, and reliability. Although a fatigue limit (at the design stage) has been used, under real-life conditions, failure occurs in the very-high-cycle regime because the high amount of reversal required for failure is necessary for high-frequency test equipment. The failure of components is reached after an expected life and normally occurs outside the guarantee period. Figure 8 shows the fatigue strength of the material using the S–N curve at different amplitudes (Figure 8a) or at different relationships between the minimum and maximum loads (Figure 8b). Composite materials are sensitive to the relationship between the minimum and maximum loads because this generates different behaviors during tension–compression, tension–tension, or compression–compression. This is due to the behavior of the fibers and depends on the characteristics of the reinforcement because there is a direct effect of the alignment of the fibers on the direction of the load.

The loads are evaluated through statistical analysis using cycle counting processes, which are used to define a summary of the loads generated by load time histories. Rainflow is used to analyze cycles from different time histories. Figure 9a shows the Rainflow cycle counting process as a function of the defined load levels. After every counting, the signal is simplified (Figure 9b) for a new counting process, and the process is repeated until a residue is reached (Figure 9c).

The goal is to define the number of repetitions that the load crosses a specific amplitude; another way to perform cycle counting is level crossing. Considering the load slope, the signal is split at different ranges, and the tendency of one crossing point to the next crossing point is evaluated. When a change is detected, the maximum value is counted, as shown in Figure 10.

After the counting process is performed with the time histories, the spectrum is defined, as shown in Figure 11. Figure 11a shows a linear spectrum for a constant amplitude load (Figure 11b). In the case of variable amplitude loads, the cycle counting generates a curve (Figure 11b), which represents the number of repetitions and different amplitudes. This spectrum is the basis for comparing a critical value (nearest to the S–N curve, the same material slope). For constant amplitude, the load amplitude (

S c

) is used, whereas for variable amplitude the critical value is used, and the whole spectrum can be simplified with different amplitude loads (

S i

). This definition makes it possible to generate the life curve of the component, and the dispersion factors must be considered to reduce the probability of failure.

The failure of the composites can be attributed to propagation in the matrix or in the fibers, as shown in Figure 12. This is generated by the accumulation process [58,66,67]. The damage generated in the components is an accumulated process derived from the number of load repetitions and the material strength under dynamic loads. Each repetition within the load history generates material degradation. The way to fail depends on the characteristics of the material; in the case of metals, most of the percentage life by fatigue is for nucleate failure, normally a crack that grows up to a critical size or a sudden failure. In composite materials, the origin and propagation of the failure will depend on the accumulated damage process. However, the failure of composite materials can originate and nucleate both in the base material (matrix) and in the reinforcing fibers. In the case of fiber failure, the material can break or bend. However, failure can also occur by a separation of the materials by having a interlaminar/intralaminar delamination, or in the transition zone.

The stiffness of some composites decreases as a function of the applied cyclic load, and a softer component is generated as a function of the fatigue life, which generates a residual strength that can be used to locate and extend damage, as shown in Figure 13 [68]. In contrast, in metals, fault nucleation develops throughout most of the life of the component. For composite materials, the fault is nucleated in the first stage, and over the course of life faults begin to develop in the matrix and/or the interface through delamination. This growth is gradual and is where a decrease in the strength of the component occurs. In the last stage, the reinforcing fibers fail, and the critical failure of the component is reached.

The evolution of the damage (

D n

) can be evaluated using a relationship between the initial stiffness (

E o

), the stiffness at failure (

E_{f}

), and the stiffness at the nth cycle (E_n), which depends on the mechanical behavior of the matrix and the reinforcement [69]. It is expressed as follows:

$D_{n} = \frac{E_{o} - E_{n}}{E_{o} - E_{f}}$

(4)

Fatigue behavior is a nonreversible damage process under cyclic loading. The failure can be evaluated using the thermal response, as shown in Figure 14, where in uniaxial fatigue tests the temperature increases until failure. Temperature is directly related to the accumulated damage process; this is because the applied loads generate mechanical energy, resulting in thermal energy. Although there is an increase in temperature due to the speed or frequency of the loads, this must avoid modifying the internal energy of the system, since the increase in temperature is an indicator of the evolution of the damage. The temperature to define a critical failure must be evaluated experimentally, since it depends on several factors such as the amplitude and characteristics of the load, the frequency or frequency range of the load spectrum, and the characteristics of the material [70,71].

The degradation of fiber strength follows a linear degradation per cycle, as in metals expressed by beach marks or chevron patterns. The residual strength (

R_{I I}^{r}

) depends on the strength of the fiber residual strength (

R_{u}^{s}

) [72] and is expressed as follows:

$R_{I I}^{r} = R_{u}^{s} - \sum_{i = 1}^{m} (R_{I I}^{s} - σ_{m a x}) \frac{Δ n_{i}}{N_{f} σ_{m a x}}$

(5)

The residual stiffness of composite materials can be defined as the relationship between the fatigue modulus (E) and the strain at the

n_{t h}

cycle [67]:

$E (n) = \frac{σ_{m a x}}{ε (n)} = \frac{q σ_{u l t}}{ε (n)}$

(6)

The critical damage (

D (n_{i})

) is defined as the damage index of failure:

$D (n_{i}) = {(\frac{n_{i} + n_{i, i - 1}^{\frac{l o g σ_{i}}{l o g σ_{i - 1}}}}{N_{i}})}^{\frac{q_{w} (1 - R)}{p_{w}}}$

(7)

$n_{i, i - 1} = N_{i} {(\frac{s i n q_{i - 1} X_{i - 1} c o s (q_{i - 1} - p_{i - 1})}{s i n q_{i - 1} c o s (q_{i - 1} X_{i - 1} - p_{i - 1}})}^{n_{i, i - 1}}$

(8)

where $X_{i - 1} = n_{i - 1} / N_{i - 1}$ , and $p_{w}$ and $q_{w}$ are weighted parameters defined by

$p_{w} = \frac{σ_{m i n}}{σ_{m a x}} (\sqrt{p_{i - 1} + p_{i}})$

(9)

$q_{w} = \sqrt{q_{i - 1} + q_{i}}$

(10)

The stress on the fiber orientation (

σ_{11}

) and its residual strength (

X_{r}

) is considered.

τ_{12}

and

S_{r}

are the shear stress and its residual strength, respectively. The fiber failure can be expressed as follows

$\frac{σ_{11}^{2}}{X_{r}^{2}} + \frac{τ_{12}^{2}}{S_{r}} = 1$

(11)

In multidirectional laminates, the fiber nucleates the failure at 0° plies, so the shear effect can be simplified to

Considering the principal stress in the transverse direction (

σ_{22}

) and its residual strength (Y_r), the failure of the matrix can be expressed as follows [73]:

$\frac{σ_{22}^{2}}{Y_{r}^{2}} + \frac{τ_{12}^{2}}{S_{r}} = 1$

(13)

The average stress and strain relations are

$ε_{12}^{*} = C_{12}^{*} σ_{12}$

(14)

$σ_{12}^{*} = S_{12}^{*} σ_{12}$

(15)

where $ε_{12}^{*}$ is the transformation strain or eigenstrain, and $σ_{12}^{*}$ is the uniform stress. $C_{12}^{*}$ and $S_{12}^{*}$ are the effective stiffness and compliance tensor, respectively, described as follows:

$S_{i j}^{*} = (V_{m} S_{i k}^{m} + V_{k} S_{i p}^{f} H_{p k}) {(V_{m} I_{k j} + V_{f} H_{k j})}^{- 1}$

(16)

$C_{i j}^{*} = (V_{m} C_{i k}^{m} + V_{f} C_{i p}^{f} T_{p k}) {(V_{m} I_{k j} + V_{f} T_{k j})}^{- 1}$

(17)

where $V_{f}$ and $V_{m}$ are the volume fractions of the fibers and matrix, respectively. $I_{i j}$ is the second-order unit tensor. $T_{i j}$ and $H_{i j}$ can be obtained [74]

$T_{i j} = {[I_{i j} + K_{i k} S_{k p}^{m} (C_{p j}^{f} - C_{p j}^{m})]}^{- 1}$

(18)

$H_{i j} = C_{i k}^{f} T_{k p} S_{p j}^{m} = C_{i k}^{f} {[I_{k q} + K_{k l} S_{l p}^{m} (C_{p q}^{f} - C_{p q}^{m})]}^{- 1} S_{q j}^{m}$

(19)

The fiber failure modes are expressed for

σ_{1} > 0

$\frac{σ_{1}}{X_{t}} - ν_{12} \frac{σ_{2}}{X_{t}} + ν_{f 12} \frac{E_{1}}{E_{2}} \cdot m_{σ f} \frac{σ_{2}}{X_{t}} = 1$

(20)

and for $σ_{1} < 0$

$|\frac{σ_{1}}{X_{t}} - ν_{12} \frac{σ_{2}}{X_{t}} + ν_{f 12} \frac{E_{1}}{E_{2}} \cdot m_{σ f} \frac{σ_{2}}{X_{t}}| + {(10 γ_{12})}^{2} = 1$

(21)

where X is the strength of the lamina under tension (t) and compression (c), respectively. The subscript f denotes the fiber properties [75,76].

4. Neural Networks in Fatigue Life Prediction

Structural degradation by mechanical fatigue has been studied for several years; however, this topic is not fully understood, and damage models are not sufficiently accurate because of the complexity of the materials [77], loads and manufacturing process [78]. Machine learning algorithms, such as artificial neural networks, random forests, and deep learning, have been used not only to emulate and predict physical behavior as material properties [79,80,81] but also for determining loads and uncertainties [82,83,84] or fatigue life in different materials, such as elastomers [85] and titanium [79,86,87]. Its learning capabilities can include defects in the training stage [88,89], which can be generated during the manufacturing process or for abuse due to random events [58,90,91,92].

The mechanism of failure depends on the stacking sequence for damage nucleation and propagation [93]. Noninvasive methods can be used to analyze the mechanical response. The modal response is an acoustic response in which changes in the microstructure modify the response [66,94,95] or the power spectral density [96]. The training models can be based on raw data or virtual data using finite element analysis and machine learning models [97,98,99,100]. These models improve the efficiency of structural health monitoring by relating the mechanical strength, the raw data and the fatigue models [101,102].

Damage detection on structures can be performed using deep learning, which analyzes the nonlinear behavior of plastic components reinforced with carbon fibers. However, some analyses, such as those performed as black boxes and to improve the prediction with a limited amount of information, are necessary to feed the network with the phenomenon-related physics, not only to reduce the expense of the training process but also to help the model predict the behavior. Fatigue damage-based stiffness degradation can be used as an input to the network to determine the relationships between and among different layers, using changes in the response as eigenvalues, time history, or frequency information using power spectral density [96,103]. Zhang and Gu proposed a machine learning model for developing composite materials through digital simulations using the minimum energy criterion as the loss function [104]. A physics-informed neural network has also been used to predict fatigue life under a multiaxial load state [105].

Machine learning, founded on statistical principles, can be employed to predict the dynamic behavior of mechanical phenomena, utilizing both raw and synthetic data for training. This information must be used to train and validate numerical models. In the case with a series of actions that are required for a final prediction, reinforcement learning is used. The characteristics of the network include neurons, the algorithm that determines how the information is processed, and the topology to integrate new numerical models through different layers from the input, analysis (hidden layers), and output layers. Neurons are connected internally and externally to transfer information and connect the previous stage to the next stage (Figure 15).

There is a relationship between a pair of neurons; this relation is the weighting coefficient that depends on the physics development, and it affects the process of obtaining different weights (w). It can strengthen or weaken the output of a neuron. The input (

I_{i}

) to a neuron is expressed by

$I_{i} = \sum_{j = 1}^{n} x_{j} w_{i j}$

(22)

A neuron cannot produce an output until it has a trigger, when the total input exceeds a threshold (

θ_{i}

), defined by

$s_{i} = \sum_{j = 1}^{n} x_{j} w_{i j} - θ_{i}$

(23)

The active value of a neuron, considering a continuous function (g), is

u_{i} = g (s_{i})

. The output of a neuron is defined by

$y_{i} = f (u_{i}) = f (\sum_{j = 1}^{n} x_{j} w_{i j} - θ_{i})$

(24)

where f is the activation function. Although the most commonly used activation function is the S form, expressed mathematically by the sigmoid function, the ramp and step functions can also be used [106].

$f (u) = \frac{1}{1 + e^{- u}}$

(25)

The connection between layers is not direct between the input and output; there are hidden layers with different configurations depending on the main target.

Although it has the ability to reproduce the relationships of complex nonlinear systems to predict the behavior of the output as a function of the inputs, the interconnection between the different layers modifies the relative weights between the different neurons, and the architecture has an effect on how this information moves to the next layer, as is shown in Figure 16. Once the network topology is defined, the relationships between the neurons are adjusted by training to learn and minimize the output error, which is performed in an iterative process until it is below a specific target. This process uses weighting adjustments and defines the proportion that propagates to the error. Back propagation networks are based on this process.

The error at the output layer depends on the expected output (

t_{k}

) and the output node (

O_{k}

), expressed by

$δ k = (t_{k} - O_{k}) O_{k} (1 - O_{k})$

(26)

where $O_{k} (1 - O_{k})$ is the derivative of the trigger function. The weights ( $ω_{j, k}$ ) are functions of the error at node k times the activation node (j), including the learning rate ( $l_{r}$ ), and the change in the weight ( $Δ W_{j, k}$ ) is defined by

$Δ W_{j, k} = l_{r} δ_{k} X_{k}$

(27)

The error at the hidden layer and the updating weight (

Δ W_{j, k}^{n}

) are summarized as follows:

$Δ W_{j, k} = l_{r} δ_{k} X_{k} + Δ W_{j, k}^{n - 1} μ$

(28)

When the error has a tendency to be minimized,

E < ε

, the learning process is finished. The general training, validation, and testing processes stop the iterative and updating processes.

$E = \frac{1}{2} \sum (\sum {(t_{k} - O k)}^{2})$

(29)

To evaluate the performance of the network, the network output is compared against the expected physical or raw response using the root mean square error:

$R M S E = \sqrt{\frac{1}{N} \sum_{i = 1}^{N} {(t_{i} - t d_{i})}^{2}}$

(30)

Another type of neural network for failure detection is the nonlinear autoregressive exogenous

(N A R X)

model, which, based on its topology that considers previous data using delays, could be useful for nonlinear responses. The topology is shown in Figure 17 and Equation (31).

$y (t) = f [y (t - 1), \dots, y (t - n_{y}, u (t - 1), \dots, u (t - n_{u} + e (t)]$

(31)

where $n_{y}$ and $u_{n}$ are the output and the past input, respectively. The delay units ( $z - 1$ ) are used to predict the next point on the input layer. The output data are computed using the bipolar sigmoid function ( $f_{1}$ ), which is expressed by

$y_{p} (t) = f_{1} (\sum_{i = 1}^{K} I w_{i} u_{i} + \sum_{j = 1}^{K} I w_{o} y_{j} + b_{i})$

(32)

The application of artificial intelligence helps predict nonlinear behaviors, such as fatigue life in composite materials. The degradation of materials generates the need to implement numerical processes that allow updating of the behavior of the material. The topology and characteristics of the neural network will depend on the available parameters that can be used as input to predict fatigue life. It is possible to include material characteristics as inputs, which can include chemical composition, and also mechanical properties such as Young’s modulus, yield stress, UTS, and strain at fracture. Fatigue can also be predicted directly by the load amplitudes and their characteristics, such as maximum effort, minimum effort, and relationship between efforts. Likewise, numerical models can be included that help the network predict durability; this can be done through nested networks including damage models. By using the results of experimental tests, the results are validated by having a low error percentage.

5. Conclusions

The battery housings of electric cars meet different conditions to protect the batteries from vibrations, impacts, and humidity. This could cause an unwanted battery reaction, but at the same time the housings protect against electromagnetic fields and in the case of fire retard the spread of flames. These loads generate accumulated damage during operation, so predicting the durability of the components is essential to prevent failures throughout the useful life of the vehicle and the battery.

Mechanical fatigue analysis is essential for predicting component failure during operation, particularly for safety-critical systems. While systems or vehicles may continue functioning until a failed component is replaced, the failure of safety systems can lead to significant risks, including damage to the mechanical components and vehicle occupants or pedestrians. Achieving sustainable mobility requires integrating advanced composite materials due to their superior weight-to-strength ratio, making them ideal for reducing vehicle weight while maintaining structural integrity. However, the long-term durability of these materials, especially in electric vehicle battery housings, remains underexplored.

Fatigue prediction in battery housings is crucial for ensuring long-term performance and preventing failures that may compromise the battery system’s operation and protective capabilities. Although AI is increasingly used to predict mechanical behavior, challenges remain, particularly in extrapolating predictions over extended lifespans and different load cases. These challenges necessitate extensive experimental testing to account for diverse driving conditions, environmental influences, and vehicle characteristics. Furthermore, AI models are data-intensive, requiring large datasets for training and validation, which presents an additional limitation.

Environmental factors and load changes are significant sources of variability in mechanical fatigue. As a component’s strength changes, the load it experiences can shift from a biaxial to a multiaxial stress state, particularly in electric vehicle battery housings. These loads come from various sources, including battery weight, vehicle acceleration forces, thermal loads, road impacts, and environmental factors, contributing to cumulative damage.

Neural networks have shown promise in improving the reliability of fatigue life predictions. However, accurate modeling must incorporate detailed information on material properties, load conditions, and manufacturing processes. Given their complexity, composite materials require precise models that reflect their anisotropic behavior and failure mechanisms, including matrix failure, reinforcement failure, and delamination. Dynamic models that update material properties based on real-time data are crucial to reducing variability and improving prediction accuracy.

The numerical model to be used to predict mechanical fatigue depends on the amount of information available or relevant to analyze the physical phenomenon. Although there are machine learning techniques that can predict phenomena more accurately, they eventually fall into overfitting because they require a large number of data. Sometimes networks such as the feedforward are better when there are few data, as is the case of mechanical properties such as the life curve (S–N), or few results for the training of the network.

The integration of AI in fatigue life prediction provides an opportunity to optimize the performance of lightweight components. However, AI models must be informed by the underlying physics of the materials rather than being treated as “black boxes”. By integrating AI with a physics-based approach, the accuracy of fatigue life predictions can be enhanced, leading to the development of lighter, more efficient components that extend vehicle range, reduce environmental impact, and allow for the recycling of components into systems with lower mechanical strength requirements.

The use of composite materials for the manufacture of battery housing for electric cars allows the development of innovative concepts to achieve the objective of reducing weight. However, an area of opportunity lies in the different recycling processes. Due to their nature, composite materials are difficult to recycle; it is important to consider the material recovery stage at the end of their useful life. Mechanical, chemical, and thermal methods can be implemented to separate the fibers from the matrix. In some cases, the matrix material can be incinerated for energy generation and at the same time the reinforcing fiber can be recovered. However, some of these processes can emit harmful gases, negatively impacting the environment.

Source link

Moises Jimenez-Martinez www.mdpi.com

Greenberg News

Battery Housing for Electric Vehicles, a Durability Assessment Review

1. Introduction

3. Fatigue in Composites

4. Neural Networks in Fatigue Life Prediction

5. Conclusions

Greenberg

1. Introduction

3. Fatigue in Composites

4. Neural Networks in Fatigue Life Prediction

5. Conclusions

Related Posts

Recycling Mystery: Oyster Shells – Earth911

Food Insecurity Is Common in Patients with Inflammatory Bowel Disease and Is Associated with Increased Ultra-Processed Food Intake

Share of natural gas production in U.S. tight oil plays increased over the last decade

Greenberg