It can be hypothesised that this faster sintering results in a significant decrease in temperature disparities between adjacent areas or layers and enhanced sinter quality. Indeed, it is around 2.5 mm of opening displacement for the XY specimens and around 3 mm for the Z specimens.
While the initial stiffness of the linear region is similar for the different processes, the peak force for crack initiation and the crack propagation response is different for each configuration. The SLS process appears to have a higher peak force for both XY and Z build directions in comparison to the MJF process. The improved interlayer adhesion of SLS achieves higher strength, while the anisotropy of the MJF process is much reduced. This is perhaps due to its high-energy laser selectively fusing powdered material, creating a denser and more homogeneous structure, while the uniform heating of the IR lamps of the MJF process reduces the anisotropy effects. However, it should be highlighted that in SLS, most of the thermal energy absorbed by PA12 comes from IR, as the bed temperature is maintained just below melting. The laser only brings the enthalpy needed to melt the polymer. It should also be noted that even though both SLS and MJF techniques use polyamide, the polymer grades are potentially different in terms of average molecular weight and polydispersity. This can itself result in different bulk mechanical properties, and care should be taken while interpreting the comparison of different manufacturing techniques.
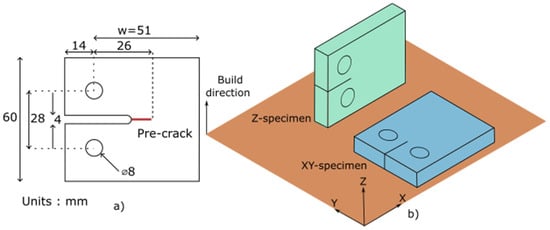
3.1. Crack Length Measurement
One of the challenges faced by researchers in fracture mechanics is the accurate estimation of the crack tip location in polymer materials, where large plastic deformation and severe necking at crack tip makes crack growth measurement difficult. However, the high resolution of the optical camera (2464 × 2065 pixels) allows to locate the crack tip position from the optical image.
Figure 8 shows the crack extension measurement using optical and thermal images. The way to measure the crack length is to take the x coordinate of the notch tip on the first optical image and to estimate the x coordinate of the crack tip during crack propagation. These measurements were realised with the ImageJ software v1.54D. The crack tip position can also be followed from the thermal images obtained during the test. The thermal images obtained from the Telops FAST M3K photon detector camera show hotspots at the location of the crack tip depicting crack propagation. The crack extension can then be measured from the identified location of the hotspot.
One of the other techniques used to measure the crack tip location is the digital image correlation (DIC) technique. The DIC technique is based on the comparison of a reference image (undeformed) and a deformed image. The surface of the object is covered in random speckle patterns and is divided into small, overlapping subsets or regions. Each subset contains a number of pixels, and the displacement of these pixels is tracked throughout the deformation process. A correlation algorithm measures the similarity between the reference subset and the subset in the deformed image. Common correlation algorithms include cross-correlation and normalized cross-correlation. These algorithms evaluate how well the pixel patterns in the two subsets match. To obtain continuous and smooth displacement and strain fields, interpolation techniques are often applied to the discrete subset data.
For this test, just one camera is sufficient because all the deformation is on the plane of the sample. The measured coordinate fields can be used to calculate quantities of interest, such as displacements, strains, strain rates, and velocities. As an example,
Figure 9 shows the shear strain component (γ
xy) on the surface of an SLS Z specimen obtained using commercial DIC software MatchID v2021.1.
The interesting thing about this DIC analysis is that the crack tip can be easily localised by looking the strain component (γxy). Near the crack tip, as one moves around the crack in a circular path, the shear strain undergoes a sign change. This sign inversion is associated with the presence of a stress singularity and is a characteristic feature of linear elastic fracture mechanics. It is important to note that these singular behaviours are characteristic of idealized linear elastic materials and assumptions. In real-world situations, especially for materials exhibiting plastic deformation or other complex behaviours, the actual stress and strain fields may deviate from these idealized patterns. In fact, it is remarkable that the line of the crack tip propagation is an axis of anti-symmetry for the strain because values of strain are opposed on both sides of this line. Moreover, the line passing through the crack tip and perpendicular to the load axis appears also as an axis of anti-symmetry for the strain. This is a good way to follow the crack evolution and a good way to study the repetitions of the stress on the surface of the materials because, by the Hooke’s law, the strain and the stress have the same sign. Therefore, the sign of the stress is changing on both sides of the crack tip.
Figure 10 shows a typical crack length vs. time graph from the compact tension tests of a polymer. The growth of the crack over time under applied loading can be observed from this curve. Initially, the crack length remains relatively stable as the test specimen undergoes initial loading. There is no noticeable crack propagation until reaching the time 550 s, when we can see the crack initiate and the lengths increase. As the test progresses, the crack length starts to increase gradually due to the applied stress. The slope of the crack length vs. time curve reflects the crack growth rate, which might vary based on factors like material properties, loading conditions, and environmental effects.
3.2. Data Reduction
The fracture parameters can be determined using either a linear elastic fracture mechanics (LEFM) approach or non-linear fracture mechanics (NLFM), depending on the mechanical response of the materials. LEFM is suitable when the material exhibits linear elastic behaviour, and the cracks are relatively small compared to the specimen’s dimensions. NLFM is chosen for non-linear materials or when large plastic deformations occur near the crack tip. The strain energy release rate is a measure of the energy required to propagate a crack in a material and is a critical parameter for understanding the fracture behaviour of materials. The area method is often employed for mode I (opening mode) fractures and is based on relating the dissipated mechanical energy ΔU to the newly generated free surface area due to crack tip advancement Δa. It is evident that the PA 12 is a ductile material, and therefore, the first idea was to modify the manner of measuring the area under the force displacement curve typically used in brittle materials to characterise a ductile fracture, given as follows:
One of the critical requirements of fracture toughness measurements based on LEFM is that plane strain conditions are satisfied. The fracture toughness KIC, which represents the material’s resistance to crack propagation under small-scale yielding, can then be calculated. In this case, the specimen thickness must be large enough to ensure that plastic deformation near the crack tip is confined, providing a conservative estimate of toughness. This condition ensures the toughness value is independent of thickness. We adopted the J-integral, which is an energy-based, path-independent contour integral used in elastic–plastic fracture mechanics (EPFM) to characterize the crack driving force in materials that exhibit non-linear (plastic) behaviour at the crack tip. The J-integral method is a widely used technique in fracture mechanics to calculate the strain energy release rate and is often employed to characterize fracture properties of materials, including polymers. The J-integral provides a path-independent measure of the energy release rate around the tip of a crack and is particularly useful in situations where the stress and displacement fields are complex. For polymers, which may exhibit ductile or tough behaviour, the J-integral method can be applied to determine critical values like the critical strain energy release rate (Gc) or the critical stress intensity factor (KIc). It assesses fracture resistance and material toughness by accounting for both elastic and plastic deformation near a crack tip. The J-integral is applicable in cases where significant plastic deformation occurs, extending fracture analysis beyond the limitations of LEFM. The J-integral can describe crack growth in both thin and thick specimens, making it useful when plane strain conditions are difficult to achieve, such as in ductile materials or thin specimens. This agrees with other researchers who have used J-integral as characterisation parameter to study fracture properties. Because of this, the normalisation method was applied to determine the J-R curves and the J integral value.
The J-integral can be divided into elastic and plastic components, and understanding their contributions is essential for characterising the fracture energy of polymers. The total J-integral is the sum of the elastic and plastic contributions:
The elastic part of the J-integral represents the energy associated with the elastic deformation of the material around the crack tip. In polymers, which can exhibit significant elastic behaviour, this component accounts for the energy stored in the material due to reversible elastic deformation during crack propagation. The elastic contribution is related to the linear elastic region of the stress–strain curve, where the material undergoes reversible deformation:
Firstly, the stress intensity factor K is evaluated using the following equation:
where
The plastic part of the J-integral represents the energy associated with irreversible, plastic deformation around the crack tip. In polymers, which often display viscoelastic and time-dependent behaviour, plastic deformation can involve not only yielding but also aspects of viscoplasticity. The plastic component is crucial for characterizing the fracture resistance of polymers, especially in cases where significant plasticity occurs during crack propagation. Polymers may exhibit strain hardening or softening behaviour, affecting the magnitude of the plastic contribution to the J-integral. The plastic part of the J-integral, is evaluated in the function of the plastic displacement
vpl and the plastic area:
In having the data and value of the crack length and evolution, the following step is to evaluate the strain energy release defined by the equation seen previously. It should be noted that the toughness values calculated using the J-integral will not necessarily correspond to KIC when plane strain is not present. However, this method acts as a means to compare the fracture toughness of the different processing methods and build orientations.
Figure 11 shows the J-R curve, which is the value of J-integral in the function of the crack length Δa of the (a) SLS specimens and (b) the MJF specimens. A comparison of the J
max of the four configurations is also shown. Comparing the two manufacturing processes, it appears that the SLS process has higher fracture values than the MJF process. Indeed, by looking at the average value of J-integral for the six samples of SLS process and for the six of the MJF one, it appears that the SLS presents values of the J-integral higher than 30% compared to that of MJF. A comparison of the build orientation for the SLS-printed samples shows that Z specimens have a J
max of about 27 kJ/m
2, which is more than double the J
max of the XY specimen (about 11 kJ/m
2). A similar comparison of the MJF-printed specimen shows that the specimen built in XY orientation has a J
max of 60% the value of the Z specimen (4.6 kJ/m
2 vs. 7.3 kJ/m
2). However, the orientation effect is less pronounced in the MJF samples compared to the SLS samples.
A more precise comparison of the value of the J-integral between the additive manufacturing processes shows that for the XY build orientation, the SLS process produces samples with a value of the J-integral higher than 60% compared to the MJF process (see
Figure 12). A similar comparison for Z models also shows that the SLS process has higher fracture properties than the MJF process. Indeed, the value of the J-integral for the SLS samples is about four times superior to the value of the MJF process.
It is possible to conclude based on the J-integral that the SLS additive manufacturing process presents higher fracture toughness than the MJF, and the Z build direction presents better results than the XY for both PBF processes. The better performance of the SLS manufacturing process may be attributed to the higher percentage of crystallinity observed in the SLS-printed samples, and it is well established that there is strong anisotropy in the stiffness and strength of additively manufactured polymers due to the layer-by-layer fabrication of AM methods [
6]. This significantly influences structural design, as the weakest direction might govern the overall strength, necessitating orientation strategies during printing to optimize performance and to ensure reliability and safety. A higher ultimate tensile strength often correlates with better fracture toughness in AM polymers, as strong inter-layer adhesion can enhance both tensile strength and resistance to crack initiation and growth. However, the relationship is not strictly linear; factors such as the presence of defects and pores, the degree of bonding between layers, and the inherent material properties also play crucial roles.
It was hypothesised that the post-condensation reaction in SLS resulted in higher molecular weight, which influenced the strength and fracture properties [
31]. The higher fracture energy of SLS Z samples is an interesting outcome. Since the laser diameter stays the same regardless of the process parameters, it may result in various outcomes when changing the layer thickness and the hatching distance. Indeed, if the layers are thin, heat penetrates further into the powder bed.
In addition, if the hatching distance is large, it may result in a lower inter-track boundary temperature. Another explanation might be related to the contours (outlines) that are generally made with different processing parameters to the infill. By default, the laser power is reduced to 16 W, and the scanning speed is slower (1500 mm/s) for the lower and upper skins. Because their number is always fixed regardless of the height or width of the sample, this results in a higher infill/shell ratio in the direction of the higher dimension. The difference in the properties of the MJF specimens built in Z orientation is perhaps due to better densification at the interlayer boundary thanks to the action of the fusing agent [
31]. Another potential explanation for the higher fracture properties in the Z direction could be the porosity and the pore network anisotropy. However, further research is required to evaluate the different hypotheses.
Numerical modelling was performed for the SLS and MJF cases in XY- and Z-direction printing and compared against the experiments in
Figure 13 and
Figure 14.
The elastic stiffness, peak load, and the failure propagation were predicted in good agreement with the experiments. Following the failure propagation and crack extension, the continuum was split into two halves, resulting in a drop in the load. The post-failure region was modelled with minimal numerical oscillations due to a combination of fine mesh discretisation and the absence of dynamic effects. Based on the results, it can be inferred that the SLS manufacturing with Z-direction printing gives the maximum peak load and energy absorption. Though unexpected, the printing direction introduces significant influence on the failure. This may be partly due to the planar specimen design.
In the Z-direction specimens, the crack propagation was normal to the build direction, and therefore, it can be inferred that breaking the sintering bonds requires the maximum load. In the XY-direction specimen, such a crack alignment was not obtained, and therefore, the failure occurred earlier.
This observation from the numerical modelling is similar to the experiments, and therefore, by understanding the failure direction for different loading conditions, this method can be used to obtain the optimal manufacturing method. The orientation of layers can create planes of weakness where cracks can initiate and grow more readily. Parts built with layers oriented perpendicular to the expected crack path tend to have higher fracture toughness, as the crack must traverse multiple layers, each acting as a barrier to crack propagation. Conversely, parts built with layers parallel to the crack path may have lower fracture toughness due to easier crack propagation along the layer interfaces.
A comparison of the shear strain contours obtained from the numerical model and experimental data is shown in
Figure 15. The cohesive zone model demonstrates good correspondence with experimental data obtained through digital image correlation (DIC), showcasing its efficacy in predicting crack growth in additively manufactured materials. The model accurately replicates crack initiation, propagation, and coalescence, aligning closely with DIC-derived measurements. This robust agreement highlights the model’s reliability in capturing the intricate mechanics of crack evolution. The synergy between cohesive zone predictions and DIC observations substantiates the model’s capability for precise crack growth simulations, offering a valuable tool for researchers and engineers in optimizing material design and structural integrity. This alignment underscores the model’s applicability and fidelity in real-world scenarios.