The emergence of electric polarizations and enhanced electrical conductivity at DWs of non-polar materials can admit many new functional devices, such as diodes, memories and switches [1,2,3]. However, so far, the progress in developing these devices has been slow, partially due to the incomplete understanding of the origins of the polarization and the lack of an efficient tuning knob for the polarization. For many materials, investigations on polarization are further complicated by the presence of defect states, multiple sources and other order parameters, such as the domain boundary and piezo-flexoelectric effect [2,4]. Generally, the induced electrical polarization upon mechanical deformation can be formulated by the constitutive equation [5,6] $P_i=e_{ijk}{\epsilon }_{jk}+{\mu }_{ijkl}{\displaystyle \frac{\partial {\epsilon }_{jk}}{\partial x_l}}$, where $e_{ijk}$ and ${\mu }_{ijkl}$ are the direct piezoelectric and flexoelectric coefficients; ${\epsilon }_{jk}$ and ${\displaystyle \frac{\partial {\epsilon }_{jk}}{\partial x_l}}$ are the strain and strain gradient. The first term describes the piezoelectric effect, the second term corresponds to the flexoelectric effect.

Recently, twisted graphene moiré superlattices are reported to be a flexible and versatile platform for observing emergent quantum phenomena, such as superconductivity [7], correlated insulator [8], ferromagnetism [9,10] and even ferroelectricity [11,12]. In the small twist angle limit, alternating non-polar stacking domains emerge due to lattice reconstruction, and the dislocations are concentrated on the boundaries between adjacent domains, leading to clean DWs with remarkable strain and strain gradient [13]. The DW width is on the order of 10 nm, falling in the mesoscopic regime. This makes twisted graphene an ideal platform for hosting piezoelectric and flexoelectric polarizations simultaneously. In practice, previous works suggest the electromechanical responses of DWs are dominated by the flexoelectric effect [14,15,16] and the piezoelectric effect [16] for tBLG and tMBG, respectively, possibly due to symmetry constraints. Our previous work presented the background-signal-free LPFM signal of a tDBG sample [15]. However, the origin of electromechanical responses for tDBG are still poorly understood.

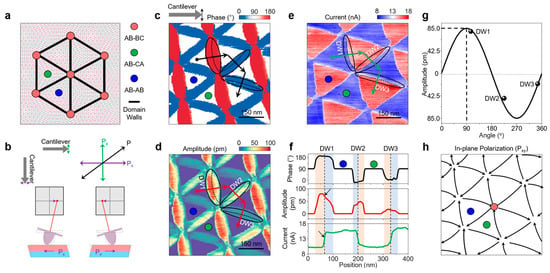
Here, two Bernal-stacked graphene bilayers twist at a small in-plane angle θ relative to each other, where the least energetically favorable configuration is AB-BC stacking (red dot, labeled from top to bottom layers and hyphens for the twisted interface), forming a moiré superlattice that maximizes the energetically favorable AB-AB (blue dot) and AB-CA (green dot) at the expense of AB-BC through lattice reconstruction [17], as shown in Figure 1a. The DWs are the ‘saddle point’ (SP) stacking (black lines in Figure 1a), also known as strain soliton [18]. In our experiment, tDBG samples consist of tDBG upon a hexagonal boron nitride (h-BN) substrate. For some samples, large graphite flakes are contacted with tDBG as electrodes, and silver paste is used to connect the large graphite electrode to the external circuit for cAFM measurements. More details about sample fabrication can be found in Figure S1 and the Methods section. The principle of LPFM is illustrated in Figure 1b, which demonstrates that LPFM can only capture the component of in-plane polarization perpendicular to the cantilever axis.

Figure 1c,d show the intrinsic LPFM phase and amplitude maps of tDBG01 recovered from the background signal [15,19] (raw LPFM results are presented in Figure S2), where only DW regions show nonzero amplitude. In Figure 1e, we show the cAFM current image of the same area where the current changes at the center of the DWs. The shape of the domains is also informative. The concave–convex alternant domains can be understood as the consequence of competition between AB-AB and AB-CA stacking orders resulting in the expansion of AB-AB domains, showing a convex domain for AB-AB and a concave domain for AB-CA [15,17]. Figure 1f shows the line cuts of LPFM phase, LPFM amplitude and cAFM current along the arrows in Figure 1c–e with expected 180° phase change.

However, the amplitude and its spatial profiles are very different from previously reported tBLG and tMBG [16]. First, the maximum amplitudes of tDBG DWs are not at the center of DWs, exhibiting two-step profile amplitude, while the amplitude of a tMBG DW only gives one peak and tBLG shows two peaks. Meanwhile, the amplitude of tDBG DWs near AB-CA domains side are much higher than that near the AB-AB domain side, as marked by red and blue background in Figure 1f. This phenomenon can be understood by the enhancement and weakness of in-plane polarization on two sides of the DW. Second, the LPFM amplitude and cAFM current change at identical positions at the DWs (dashed lines in Figure 1f). The cAFM measurement is highly sensitive to the local stacking of tDBG moiré superlattices [20,21,22,23], and an LPFM measurement can capture its in-plane polarization. Hence, the dashed lines indicate the precise SP locations between the AB-AB and AB-CA stackings, where electromechanical and electric properties change simultaneously. Specifically, for DW1, the amplitude gives a drop from 75 pm to 50 pm, while the current presents an increase from 10.3 to 15.5 nA, as marked by black arrows. The amplitudes of three tDBG DWs satisfy a sinusoidal relation (Figure 1g), which matches well with previous tMBG and tBLG results [14,16]. From the angle-dependence LPFM results of tDBG02 (see Figure S3), Figure 1h gives the in-plane polarization networks of tDBG01, which is consistent with previous tDBG results [15].

This two-step profile phenomenon can be enhanced by adjusting measurement parameters, e.g., drive frequency and cantilever-sample force. More details about the frequency-dependent LPFM amplitude of tDBG can be found in Figure S4. Figure 2a,b show the LPFM results of tDBG03 (see raw LPFM phase and amplitude images in Figure S5); its amplitude gives a clearer two-step profile than Figure 1d. Figure 2c presents line cuts of phase and amplitude along red and black arrows in Figure 2a,b. Mathematically, this two-step profile LPFM signal (red line) of DW4 can be divided into an axisymmetric vector (green line) and a centrosymmetric vector (blue line), as illustrated in Figure 2d. Hence, the axisymmetric and centrosymmetric components of line cuts in Figure 2c can be calculated, as shown in Figure 2e,f. Those decoupled LPFM results are similar to those of tMBG and tBLG in the following two aspects. First, both the axisymmetric component of tDBG and tMBG show one broad peak, and the centrosymmetric component of tDBG and tBLG give two extrema with 180° phase change. Second, the amplitudes of axisymmetric and centrosymmetric components for three DWs (DW4, DW5 and DW6) satisfy sinusoidal relations (Figure 2g), which is a typical feature for in-plane polarization [14,16]. Apart from similarity, the magnitude of the axisymmetric component of the tDBG LPFM amplitude is only twice as much as that of the centrosymmetric component, while the amplitude of tMBG is about an order of magnitude larger than that of tBLG. These similarities and differences among tBLG, tMBG and tDBG are reminiscent of the in-plane electrical polarization of tDBG generated by the combination of piezoelectric and flexoelectric effects. Noteworthily, the two-step profile is highly sensitive to scan parameters. Figure S6 shows another LPFM scan of the same area in Figure 2a,b with different drive frequencies, which gives a single-peak profile. This sensitivity to scan parameters is also shown in the tBLG sample [16].

To obtain the in-plane piezoelectric coefficients of DWs in tDBG, we performed DART LPFM measurements on tDBG04, and the typical DART LPFM amplitude and phase (decoupled from the background) maps of tDBG04 are presented in Figure 3a,b with an expected 180° phase change and three different amplitudes. One peak profile is captured in the DART LPFM measurements because the two-step profile is dependent on the scan parameters. Moreover, the centrosymmetric component of the LPFM signal has no contribution to the LPFM amplitude. Zooming in on the white dashed boxed area in Figure 3a, Figure 3c shows selected five DART LPFM amplitude maps of tDBG as the drive voltage increases from 1 V to 4.5 V (see Figure S7 for details), in which the amplitude increases significantly. Figure 3d presents the averaged amplitudes at three DWs of tDBG04 (DW7, DW8 and DW9 are marked by red, blue and green dashed polygons in Figure 3c) as a function of the drive voltage, respectively, along with their linear fits. The three fitted slopes are the three projected in-plane piezoelectric coefficients of a DW. Only when the cantilever axis is perpendicular to the DW is the fitted slope equal to the in-plane piezoelectric coefficient of the DW, except when setting sample-cantilever angle as 90°, as the in-plane piezoelectric coefficient can also be extracted by the sinusoidal fitting of the three slopes, as illustrated in Figure 3e. Consequently, the in-plane piezoelectric coefficient of a DW in tDBG is determined to be 0.15 pm/V, which is three times larger than that of tBLG and half that of tMBG [16].

We employ continuum mechanics theory to explain the two-step LPFM profile of tDBG. When a conductive tip-induced electric field $E_k$ is applied to the DWs of twisted graphene with an electrical polarization $P_v$, the induced strain ${\epsilon }_{ij}$ can be expressed as [24] ${\epsilon }_{ij}=k_{im}{Q}_{jkmv}{P}_v{E}_k$, where $k_{im}$ is the dielectric constant, and $Q_{jkmv}$ is the electrostrictive coefficient. For ideal tDBG moiré superlattices, the moiré DW is shear-type along the y axis [23], as shown in Figure 4a, where $u_y$ is the only nonzero displacement. Thus, only ${\displaystyle \frac{\partial u_y}{\partial x}}$ and ${\displaystyle \frac{{\partial }^2{u}_y}{\partial x^2}}$ need to be taken into consideration. In Figure 4b(i), we sketch the profile of the displacement across the DW, where the profile of the displacement was adopted from Ref. [25]. For a linear constitutive relation, the in-plane piezoelectric (Figure 4b(ⅱ)) and flexoelectric (Figure 4b(ⅲ)) polarizations show axisymmetric and centrosymmetric profiles, respectively. Surprisingly, the linear combination of piezoelectricity and flexoelectricity gives a two-step profile (Figure 4b(ⅳ)), which is highly consistent with the LPFM signal of tDBG; we call it ‘piezo-flexoelectricity’. Based on the threefold rotational symmetry of tDBG, a two-dimensional map of the in-plane piezo-flexoelectric polarization is presented in Figure 4c. The AB-CA domains surround the in-plane polarization clockwise, and AB-AB domains enclose the in-plane polarization anticlockwise, while the magnitude of in-plane polarization near the AB-CA domain is larger than that of the AB-AB domain.