1. Introduction
Access to reliable and high-quality climate information is essential in coping with current and future climate variability and change [
1]. The availability of accurate precipitation data is of fundamental importance for applying hydrologic models for purposes such as water resource management, irrigation planning, hydropower operations, and forecasting of floods and droughts [
2]. Accurate precipitation data are also needed for calibrating remote sensing products [
3] and climate models [
4] to facilitate future projections.
Particularly in high mountainous regions, climate information is often highly uncertain. The complex terrain and orographic effects cause high spatiotemporal variability in precipitation [
5,
6] which is often not captured by the comparatively few climate stations. For example, in the Tarim River basin in northwestern China, climate stations are predominantly located in the lowlands and in the valleys of the mountains, where access is easy; very few stations are present at higher elevations [
7,
8]. Scarcity of climate data has also been reported from the Asian Himalayas [
9,
10,
11] and the Tibetan Plateau [
12,
13] and from the South American Andes [
6,
14], the African Atlas mountains [
15,
16] and the Ethiopian highlands [
17].
Particularly in regions where in situ ground observations are scarce, reanalysis data often seem to be the best option. Global reanalysis datasets are globally complete and are therefore sometimes referred to as “maps without gaps” [
18,
19]. After previous research in the 1980s [
20,
21], concentrated efforts have been made to generate multi-year global reanalyses since the early 1990s [
22,
23]. A retrospective analysis, also known as reanalysis, is produced via a frozen data assimilation system and numerical weather prediction model [
24] that, by ingesting available observations, achieves hindcasting [
25]. The goal of a climate reanalysis is to generate consistent and accurate climate datasets for a longer period.
Global reanalyses not only provide global spatial coverage; they also do not have gaps in time series. However, the reliability of the reanalysis data varies in time and space. If no in situ observations are available for a region, the quality of the reanalysis will be reduced, especially in that region. In situations where observations are missing, the reanalysis relies on imperfect information; therefore, as reanalysis data are available for regions where ground observational data are scarce, their limitations should be known and accounted for [
26].
Another reason that reanalysis data are attractive is the enormous number of atmospheric variables available. The first global atmospheric reanalysis provided by U.S. agencies, the National Center for Environmental Prediction/National Center for Atmospheric Research Reanalysis 1 (NCEP/NCAR R1), already offered numerous atmospheric variables on multiple vertical levels. In addition to air temperature and geopotential height at 17 levels, many other variables such as relative humidity of the total atmospheric column, runoff, potential evaporation rate, water equivalent of accumulated snow depth, and precipitation rate were provided; some of these variables, such as air temperature and geopotential height, were designated as type A variables in NCEP/NCAR R1, indicating the most reliable class that is strongly influenced by observed data [
22]. Precipitation rate was classified as a type C variable that is completely determined by the model [
22] and thus should be used with caution [
27]. In some of the more modern reanalyses, for example, in MERRA-2, precipitation observations are used in the assimilation process [
28,
29], possibly making precipitation rates more realistic.
One of the difficulties in working with reanalysis data is that the accuracy of reanalysis results is less well understood compared to the accuracy of observations [
30]. Given the large number of reanalysis projects, it is challenging to find the most appropriate reanalysis with which to answer a research question, as there is uncertainty in any given reanalysis.
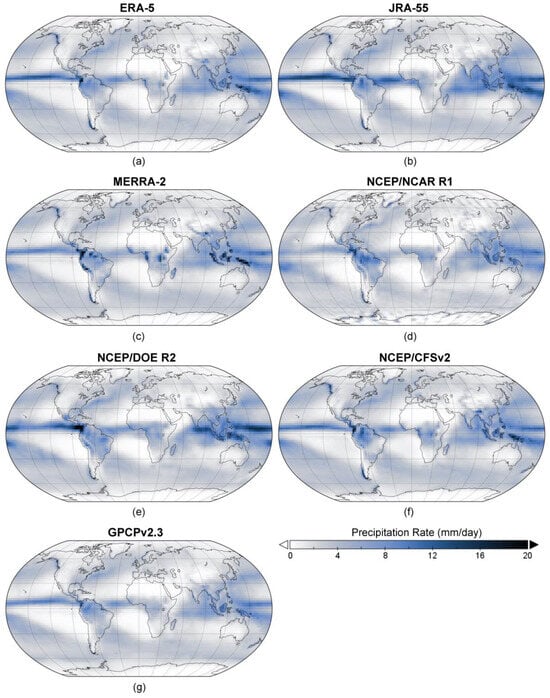
How large are the spatiotemporal differences between precipitation rates from reanalysis datasets and a precipitation dataset that is based on in situ observations and information from satellites? To allow for a more educated choice in the usage of precipitation data, especially in areas where in situ observational data are sparse, this paper compares precipitation rates from five reanalysis datasets and one analysis dataset with precipitation data from a merged satellite and rain gauge dataset.
4. Discussion
The first point that shall be discussed here is the reliability of the reference dataset GPCPv2.3. The key limitations of GPCPv2.3 listed in Pendergrass et al. [
57] include the existence of residual inter-satellite differences at the boundaries between the areas of coverage of the geo-infrared sensors as well as the potential bias in precipitation estimates resulting from significant drifting of the equator-crossing time of some polar-orbiting satellites during their period of service. Based on global water and energy budgets, it was concluded that GPCPv2.3 underestimates precipitation specifically over the ocean [
63]. Furthermore, the spatial resolution of 2.5° restricts the usage of the dataset. As mentioned in the introduction, particularly in high mountainous regions, the terrain is complex, and orographic effects cause high spatiotemporal variability in precipitation [
5,
6], which cannot adequately be captured given this spatial resolution of the dataset. The monthly temporal resolution is another limiting factor. For hydrological modeling, even in data-scarce regions, the precipitation data are used in at least daily resolution [
64].
Despite its limitations, GPCPv2.3 has been used as a reference dataset in many studies such as those of Beniche et al. [
65], Anochi et al. [
66], Sharma et al. [
67], Nogueira [
68], Li et al. [
69], and Hassler and Lauer [
70]. In the study by Beniche et al. [
65], precipitation data from GPCPv2.3 were used to evaluate the impacts of El Niño Southern Oscillation events on precipitation over North America and the Pacific. In that by Anochi et al. [
66], the GPCPv2.3 dataset was employed as a target with which to train machine learning models and to validate precipitation forecasts for South America. The GPCP precipitation dataset was used as ground truth for correcting Indian Summer Monsoon Rainfall as simulated by the Indian Institute of Tropical Meteorology climate forecast system over the Indian subcontinent [
67]. In Nogueira [
68], GPCPv2.3 was the reference used to evaluate the performance of ERA-5 and ERA-Interim precipitation worldwide.
From the studies in which GPCPv2.3 was used as a reference dataset, the results from Li et al. [
69] and Hassler and Lauer [
70] are most comparable to the ones of the present study.
Li et al. [
69] evaluated among other things the performance of precipitation data from ERA-5, JRA-55, MERRA-2, and the CFSR against GPCPv2.3. Looking at the time period from 1980 through 2018, they found that all datasets except MERRA-2 show wet biases in precipitation over tropical regions, particularly over the Pacific and Atlantic region of the Intertropical Convergence Zone (ITCZ). Similar to the maps from the correlation analyses presented in this study, their maps depicting calculated correlation coefficients between the annual precipitation anomalies in the different precipitation datasets and GPCPv2.3 annual precipitation anomalies show areas of no correlation for the eastern (dry region) boundaries of the Pacific and Atlantic ocean basins.
In the study by Hassler and Lauer [
70], GPCPv2.3 was compared with 10 other precipitation datasets, of which 6 were from reanalyses and 4 were from observational datasets. The comparison focused on the Tropics, the Pacific ITCZ, Central Europe, and the South Asian Monsoon region for the time period from 1983 through 2016. Similar to the results of this study, they found that ERA-5 for the most part agrees better with GPCPv2.3 than MERRA-2 and JRA-55. As in the present study, a strong overestimation of tropical precipitation was found particularly for JRA-55 (especially over the ocean) but also for MERRA-2 (especially over land) and to a lesser extent for ERA-5.
In an older study from Quartly et al. [
71], correlation coefficients between GPCPv2 and NCEP/NCAR R1 as well as between GPCPv2 and NCEP/DOE R2 were calculated for the period from 1979 to 2000. The study focused on the ocean and found generally lower correlations between NCEP/DOE R2 and GPCPv2. Quartly et al. [
71] also detected much higher precipitation in NCEP/DOE R2 over the ocean as compared to NCEP/NCAR R1 and GPCPv2. Looking at the maps depicting Spearman correlation coefficients from the present study, it becomes clear that even though our mean correlation coefficient between NCEP/DOE R2 and GPCPv2.3 is slightly higher, the correlation over the ocean is lower as compared to NCEP/NCAR R1 and GPCPv2.3. The strong overestimation of precipitation in NCEP/DOE R2 is also evident in the present study, especially over the tropical ocean.
As the focus of this study is on providing guidance in the choice of precipitation data, for example, for hydrologic modeling, the following paragraphs provide advice based on the results presented in
Section 3. The recommendations made here are valid for the period from January 2019 to December 2023.
Precipitation rates from ERA-5 and JRA-55 showed very small deviations from the reference dataset GPCPv2.3 over Europe and eastern South America. In the absence of ground observational data, the use of precipitation data from both datasets seems acceptable in these areas. Over Australia, similarly small deviations were found between precipitation rates from ERA-5 and the reference dataset, as well as between NCEP/CFSv2 and the reference dataset. Using precipitation rates from ERA-5 and NCEP/CFSv2 in Australia seems feasible if no ground observational data are available. ERA-5 also performed well over Central and North America in all areas south of 40° north. In the absence of ground observational data, applying precipitation rates from ERA-5 could be an option. Over the North Atlantic and North Pacific Ocean basins that are south of 70° north, precipitation rates from MERRA-2 closely resembled the reference dataset. The same is true over the Indian Ocean basin and western South Pacific and over the extratropical eastern South Pacific and South Atlantic north of 65° south. In these areas, MERRA-2 performed best closely followed by ERA-5. In the case that no ground observational data are available, the use of precipitation data from MERRA-2 is recommended here.
For many regions with sparse precipitation, high percentage errors between the different datasets and the reference dataset were found. Therefore, replacing ground observational data with precipitation rates from the datasets presented here is generally not recommended. These regions include the Tibetan Plateau, parts of Central Asia, southern Patagonia, the Atacama desert, the Sahara desert and the Sahel, western Greenland, East Antarctica, and the oceanic regions of sparse precipitation along the west coasts of southern Africa and of South America. As the absence of ground observational data in many of these regions may force researchers to find alternative data sources, I will list for each of these regions which precipitation dataset performed better than the others (although not performing well).
Over the Tibetan Plateau and Central Asia, precipitation rates from ERA-5 and NCEP/DOE R2 showed the smallest (but still considerable) deviations from the reference dataset. Over southern Patagonia, NCEP/NCAR R1 and NCEP/DOE R2 performed better than the other datasets. Precipitation rates over the Atacama desert were comparatively satisfactorily represented by ERA-5 and JRA-55. Over the Sahara desert and the Sahel, precipitation rates from ERA-5 showed the smallest deviations from the reference dataset. Over western Greenland and East Antarctica, JRA-55 and NCEP/DOE R2 performed better than the other datasets. Compared to the other datasets, NCEP/NCAR R1 satisfactorily represented precipitation rates over the oceanic region along the west coast of southern Africa. The same is true for JRA-55 over the oceanic region along the west coast of South America.
5. Conclusions
Particularly in data-sparse regions, it is tempting to use precipitation rates from reanalysis datasets in hydrologic modeling. However, it needs to be taken into account that the reliability of reanalysis data varies in time and space and differs according to climate variables. Precipitation rates are among the more uncertain variables in reanalysis datasets, especially in the first generation of global reanalyses such as NCEP/NCAR R1. It is advisable to check for the limitations of precipitation data, especially from reanalysis datasets, prior to their application. In this study, precipitation rates from the reanalysis datasets ERA-5, JRA-55, MERRA-2, NCEP/NCAR R1, NCEP/DOE R2, and the analysis dataset NCEP/CFSv2 were compared with precipitation data from the merged satellite and rain gauge dataset GPCPv2.3 over the period from 2019 to 2023.
Overall, the precipitation rates from ERA-5 agreed best with the GPCPv2.3 reference precipitation data: the smallest mean and maximum percentage errors, the highest mean correlation, and the smallest mean RMSE were found for ERA-5. ERA-5 performed well over Europe, Australia, and southern North America. However, even though the performance of ERA-5 can be considered the best overall, there are still regions in which the application of precipitation rates from ERA-5 cannot be recommended. These regions include the Tibetan plateau and parts of Central Asia, western Greenland and East Antarctica, the Atacama desert, southern Patagonia, the Sahara desert and the Sahel, and the oceanic regions with sparse precipitation along the west coasts of South America and southern Africa. It shall be mentioned here that even though ERA-5 showed considerable deviations from the reference dataset in the above-mentioned regions, it still performed better than the other datasets over the Sahara desert and the Sahel, as well as over the Atacama desert, the Tibetan Plateau, and Central Asia.
JRA-55, MERRA-2, and NCEP/CFSv2 all performed well over the eastern part of North America and Europe. MERRA-2 also performed well over the Indian Ocean basin, and NCEP/CFSv2 exhibited good agreement with the reference dataset over Australia. However, these three datasets performed poorly in several other regions. JRA-55 overestimated precipitation over the tropical ocean, and MERRA-2 did so over tropical land regions. NCEP/CFSv2 overestimated precipitation in different geographical regions over land including the Malay Archipelago, the region south of the Himalayas, and southern Patagonia.
Even though NCEP/NCAR R1 showed the smallest mean differences from the reference dataset and therefore also the closest value for mean total global precipitation, the use of precipitation rates from NCEP/NCAR R1 generally cannot be recommended. Precipitation rates from NCEP/NCAR R1 showed the highest mean and by far the highest maximum percentage errors as well as the lowest correlations with GPCPv2.3. The precipitation rates from NCEP/DOE R2 were significantly higher than the reference dataset, and their usage is also not recommended. Precipitation rates from NCEP/DOE R2 exhibited the second lowest correlations with precipitation rates from GPCPv2.3 and the highest mean RMSE.