A special role in biomedicine is played by magnetic nanoparticles (MNPs) with a wide range of functionalities, derived from their material nature, structure, and morphology; magnetic properties; and chemical affinity to biomolecules of medical interest [1,2]. A crucial condition that must be fulfilled in biomedical applications is the biocompatibility of the materials involved. The interaction between MNPs and biomolecules has opened a wide area of applications in biomedical fields, such as magnetic hyperthermia and drug delivery, used in cancer therapy [3,4], biomedical sensing [5] and imaging, etc. [6]. “Cancer” refers to the uncontrolled cellular growth in specific tissues that enhances angiogenesis and the formation of metastases [3,7]. Most cancers are associated with genetic alterations that affect the regulation of cellular growth. The treatment of cancer mainly focuses on stopping the chaotic cellular replication process through drug administration (cytostatic), which generally has a low degree of uptake by the malignant cells and aggressive side effects [8]. A novel way to solve this issue is to bind cytostatic molecules to MNPs, which can be directed by various procedures, including magnetic fields, to the target tumor. Following the uptake process in tumor cells where the MNPs are directed, i.e., by maintaining healthy cells almost unaffected [9,10,11,12,13], this treatment becomes more localized, efficiently releasing the drug molecules into the cells. Generally, many routes have been developed for targeting tumors through recent nanotechnology advances in the biomedical field. Drug carriers like polymeric nanoparticles, liposomes, viral and gold nanoparticles, carbon-based systems, and magnetic nanoparticles (e.g., iron oxides) were developed to optimize biomolecule transportation into cancer cells [14,15,16,17]. There are two targeting approaches for antitumor agents as follows [3,18,19,20]: (i) passive targeting, generated by the enhancement of permeability and the retention (EPR) effect, which allows the accumulation of high-molecular-weight molecules and fine particles (diameter ~20–500 nm) within the tumor tissue due to a leaky vasculature (notably, this targeting method has a universal role in treating different types of cancers using the same drug delivery system); and (ii) active targeting, involving the chemical bonding between membrane receptors from targeted cells and additional ligands bound on the surface of the drug carrier. Drug molecules used in cancer treatment are not easily bound to the surface of nanoparticles because of their lack of chemical affinity. Instead, an organic layer with a high affinity for the biomolecules of interest usually covers the surface of the nanoparticles. Depending on the type of cytostatic, specific organic layers must be used with respect to the biocompatibility conditions. Doxorubicin, a widely used drug in cancer treatment, has proven to be highly effective [21,22,23,24]. It treats various solid tumors, acting through multiple mechanisms [25]. It is important to note that depending on the dose, doxorubicin may induce cardiotoxicity, especially in a cumulative dose regime [26]. Therefore, the sensitive evaluation and control of drug loading is crucial for optimizing clinical treatment doses. There are specific methods for the evaluation of drug loading capacity such as analytical chemistry methods (high-performance liquid chromatography—HPLC [27,28]) or IR spectrophotometry techniques [29,30,31]. However, such methods focus more on the drug release capacity, which is not always straightforwardly related to the drug loading capacity. On the other hand, the advantage of using MNPs as nanocarriers of drug molecules is not only due to the additional targeting possibilities intermediated by specific configurations of applied magnetic fields but also due to the ability to finely control drug release through hyperthermia activation using low amplitude ac magnetic fields, which can superpose, in certain circumstances, with the localized curing effect introduced by the hyperthermia process itself. In this respect, the change in the magnetic properties of the core MNPs induced by the presence of medicine molecules might also become important.

This work presents an innovative methodology for quantifying the drug loading capacity of iron oxide-based MNPs by corroborating magnetometry and Mössbauer spectroscopy investigations. In a previous work [30], the doxorubicin cytostatic used in the treatment of melanoma was bound on the surface of magnetite-like MNPs through L-Cysteine molecules and tested in vitro on mouse 16F10 and human A375 metastatic melanoma cells. Following this, the proposed methodology is applied on two sets of iron oxide MNP systems, as follows: (i) Fe₃O₄ MNPs covered with Citric Acid (CA) and functionalized with doxorubicin and (ii) Fe₃O₄ MNPs covered with L-Cysteine (LC) and also functionalized with doxorubicin. Superconducting Quantum Interference Device (SQUID)-based Magnetometry and Mössbauer spectroscopy measurements of naked and successively loaded (by CA, CA&Dox, LC, and LC&Dox) Fe₃O₄ MNPs revealed the main information about the mass magnetization (in emu/gram) and magnetic structure on the nanoparticles’ surface, as influenced by the attached molecules. The evolution of saturation magnetization imposed by the non-magnetic loading is corroborated with the change in the magnetic state of the core of the MNPs in order to extract valuable information on their loading with medicine molecules.

A complex structural and morphological characterization of all obtained samples has already been reported in [30,32] and therefore only the conclusion of interest for this work will be resumed here. In the case of naked Fe₃O₄ MNPs, similar broad size distributions ranging from 3 nm to 20 nm were evidenced in all preparations, with two types of morphologies as follows: spherical shape (for the finest particles) and faceted shape of a cubic or rhombohedral type (for the larger ones). Notably, a change in the morphological parameters (e.g., a slightly larger size distribution extending up to 30 nm) was observed only for the Fe₃O₄@LC@Dox MNPs, indicating the possible influence of the covering organic molecules on the magnetic configuration of the inorganic core only for this branch of samples.

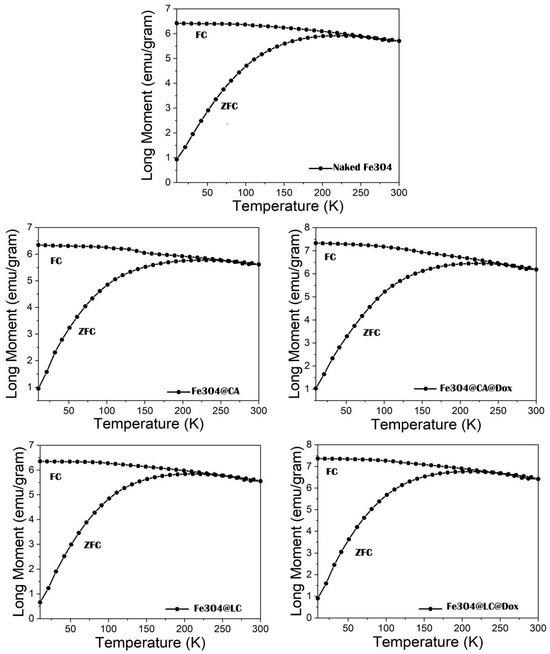
The ZFC–FC measurements from 10 K to 300 K in 100 Oe show a broad maximum on the ZFC curve in the range of 190–230 K, depending on the investigated samples (see Figure 1). So, blocking temperatures, T_B ranging from 210 to 222 K for different samples can be found from the maximum of the ZFC curves (see Table 1 and Table 2). Notably, T_B represents the temperature where the transition from the magnetically frozen regime to the superparamagnetic regime of MNPs takes place within the time windows of the measuring method (e.g., this is in the range from 1 to 100 s in the case of magnetic measurements). The flat shape of this maximum, along with the smooth divergence of the ZFC and FC curves, points to a wide distribution of the anisotropy energies (KV) of MNPs, where K is the anisotropy constant, and V is the volume of MNPs. However, the FC curve always develops over the ZFC curve, supporting the nature of magnetic monodomain nanoparticles. These results not only reveal the very broad size distribution of the naked and functionalized MNPs, especially extended at larger sizes (please see the findings confirmed by previous TEM investigations, according to [30]), but also quite similar magnetic relaxation phenomena that are specific to all investigated systems.

Due to the weak decrease in the magnetization curves between the branching point and 300 K, it can be assumed that only a fraction of the MNPs reached the superparamagnetic regime at 300 K, with the rest remaining in the frozen regime. According to the hysteresis loops presented in Figure 2, the coercive fields decrease from about 300 Oe at 10 K to about 15 Oe at 300 K for all samples. The very low value of the coercive field at 300 K, not specific to well-structured magnetite, represents additional proof that at this temperature, the system consists of a superposition of superparamagnetic and magnetically frozen MNPs. Magnetic hysteresis loops at 10 K show a saturation magnetization between 52 and 63 emu/g for all samples, values which are approximately 30–40% lower than the saturation magnetization of well-formed Fe₃O₄ nanoparticles [33]. Notably, the saturation magnetization obtained at the lowest temperature of 10 K (full magnetic frozen regime) provides the best estimation for the spontaneous magnetization, which can be directly connected with the real magnetic structure of MNPs. A law of approach [34] has been used for the sensitive evaluation of saturation magnetization, as indicative of the spontaneous magnetization values reported in Table 1 and Table 2.

The obtained low value of the saturation magnetization at 10 K indicates the formation of a quite defect magnetite phase or even the progressive formation of a maghemite phase at the particle surface (the maghemite is itself an intrinsically defect magnetite with cation vacancies [35]). Such a crystalline defect structure may lead to a magnetic defect structure at the particle surface, which, on one side, decreases the saturation magnetization and, on the other side, is sensitive to the surface molecules chemically bound to the nanoparticle (NP) surface. To provide complementary information on the magnetic structure of naked and functionalized MNPs, low-temperature Mӧssbauer spectra were recorded for all samples. Contrary to the magnetic data showing almost no difference between ZFC-FC and as well as between hysteresis loops for the naked Fe₃O₄ in the two series, slight differences between the magnetic relaxation phenomena within the Mössbauer time window (10⁻⁹ s) were observed, as subsequently discussed.

The spectra collected at three temperatures (6 K, 100 K, and 200 K) for naked Fe₃O₄ and NPs loaded with L-Cysteine and L-Cysteine and doxorubicin (Fe₃O₄@LC, Fe₃O₄@LC @Dox), as well as for a second series of naked Fe₃O₄ NPs and NPs loaded with citric acid and citric acid and doxorubicin (Fe₃O₄@CA and Fe₃O₄@CA@Dox), are shown in Figure 3.

The Mӧssbauer spectra at the lowest temperature of 6 K consist, in all cases, of a broad sextet, as expected in the case of Fe oxide MNPs, with distributed configurations of Fe ions. The sextets become even broader at increasing temperatures, showing collapsing behavior that starts at 200 K and is specific to MNPs in the magnetic relaxation regime. This aspect leads to the possibility of having a unitary fitting of all spectra at increasing temperatures via a distribution of magnetic hyperfine fields, according to the algorithm proposed in [36]. The probability distribution of magnetic hyperfine fields is shown on the right side of each spectrum. At a glance, Figure 3 shows the similar collapsing behavior of naked Fe₃O₄ NPs and NPs functionalized with CA (Fe₃O₄@CA and Fe₃O₄@CA@Dox). On the other hand, naked Fe₃O₄ NPs and NPs functionalized with LC (Fe₃O₄@LC and Fe₃O₄@LC@Dox) show a different collapsing behavior, which is also different among the three samples. This shows a clear difference in the magnetic structure of the two series of functionalized samples, which also gives a first hint for adding new magnetic spectral components in the MNPs functionalized with LC, as compared to the ones functionalized with CA. The evolution of the average magnetic hyperfine field, _hyp>, versus temperature, as presented in Figure 4, can also be considered for a quantitative comparison of the two series of samples.

On the other hand, as evidenced by the 200 K Mӧssbauer spectra, the magnetic relaxation of the naked Fe₃O₄ NPs in the first series is slightly enhanced compared with the corresponding naked Fe₃O₄ NPs in the second series, under an almost identical magnetic hyperfine field value of 6 K and spontaneous magnetization. In these peculiar conditions, which suggest similar magnetic configurations of naked Fe₃O₄ NPs (e.g., similar magnetic configuration and K anisotropy constant) in the two series, the only explanation for the slightly faster relaxation of the naked MNPs in the first series is a slightly lower (e.g., by a few percent) average size of Fe₃O₄ NPs in this series, as compared to the Fe₃O₄ NPs in the second series. This aspect is not entirely unexpected given the criticality of NP size distribution on the processing conditions. However, such small differences in the size distribution of naked Fe₃O₄ NPs in the two series cannot be possibly evidenced by either TEM or SQUID investigations but only via the magnetic relaxation behavior within very short time windows, which is specific to Mӧssbauer spectroscopy. In the context of the high sensitivity of the Mӧssbauer spectra on the magnetic relaxation phenomena, the most proper investigation concerning the differences between the magnetic configuration of MNPs should be carried out at the lowest temperature of 6 K, where the MNPs are in a complete magnetically frozen regime (see Figure 5).

Concerning the Fe oxide MNPs in the first series, all spectra (Figure 5a–c) have been fitted by a highly dominant broad sextet component (over 98% relative area contribution), which is specific to distributed Fe configurations in a defect-like spinel structure of magnetite/maghemite type. The corresponding average isomer shift is similar in the case of all three samples in the series (naked Fe₃O₄, Fe₃O₄@CA, and Fe₃O₄@CA@Dox), i.e., 0.45(1) mm/s. This is the same with the average magnetic hyperfine field, i.e., 51.0(2) T, and the distribution width at half maximum, i.e., 6.4(2) T, which are the same for all samples in the series. These parameters point to MNPs of almost identical magnetic configurations in all three samples in the series, namely configurations based on Fe³⁺ ions in the high spin state of S = 5/2, i.e., with a defect spinel structure more closely resembling that of a maghemite. An almost insignificant central doubled component (less than 2% relative area contribution) was also considered for improving the fit quality in all spectra. This component can be associated with the specific hyperfine parameters (quadrupole splitting of 2.4(1) mm/s and isomer shift of 1.00 mm/s) to approximately less than 2% Fe²⁺ ions, most probable in very fine Fe oxide clusters, which are already superparamagnetic at 6 K. A negligible contribution to the magnetic state of the sample is expected from this less than 2% phase, which is however the same in all three samples. In this context, the almost identical Mӧssbauer spectra of the three samples in the series clearly prove that covering molecules does not change the magnetic configuration at the nanoparticle surface. While the Fe ions are the only magnetic ions, the conclusion is that CA molecules stick to the surface of MNPs, either by physical adsorption or by chemical bonds to the oxygen ions in the Fe oxide NPs. However, independent of the sticking mechanism, the conclusion of the Mössbauer investigation of the first series of samples is that the covering molecules do not affect the magnetic state of the core NPs. Therefore, the spontaneous magnetization of the magnetic core is the same for uncoated and surfacted MNPs, i.e., identical with the spontaneous magnetization of naked Fe₃O₄ (see Table 1). Hence, any variation in the spontaneous magnetization of the samples consisting of covered MNPs is strictly due to the amount of organic layers present in the sample. If M*_S is the spontaneous magnetization of the magnetic component (equal in this case to the spontaneous magnetization of naked Fe₃O₄ NPs) and M_S is the spontaneous magnetization of the covered MNPs, the amount of surface molecules (in grams) is straightforwardly obtained as

Notably, in reference [32], we have reported both the loading efficiency and the loading capacity with Dox molecules for the same Fe₃O₄@CA@Dox system by analyzing the amount of residual drug in the solution using spectrophotometry at 480 nm. Defining the loading capacity as the ratio between the amount of released drug and the total amount of nanoparticles (expressed as a percentage), a maximum value of 10(1)% was obtained for this system (prepared with 80 ppm Dox concentration), which is in very good agreement with the value reported in the present paper, reporting 0.11 g of Dox per g of coated Fe₃O₄@CA@Dox NPs.

Concerning the Fe oxide MNPs in the second series, the 6 K spectrum of naked Fe₃O₄ MNPs is very similar to the case of naked Fe₃O₄ MNPs in the first series (see Figure 5a,d) and has, therefore, been fitted accordingly. A first clear difference appears in the case of the 6 K spectrum of sample Fe₃O₄@LC (see Figure 5e) where an asymmetrically split sextet (7(1) % relative spectral area) has to be added to the main broad sextet (93(1) % relative spectral area) for a proper fit. Note that the hyperfine parameters of the main broad sextet are very similar to the ones for the naked Fe₃O₄ MNPs, pointing to the presence of Fe³⁺ ions in the high spin state S = 5/2. The hyperfine parameters assigned to the additional sextet are as follows: an isomer shift of 0.12(3) mm/s, a quadrupole splitting of 0.90(3) mm/s, and a magnetic hyperfine field of 31.0(1) T. These values are specific to Fe³⁺ ions in the intermediate spin state S = 3/2 [35] and lead to the conclusion that the LC coating molecules affect the magnetic state of the MNPs, most probably by changing (via chemical bonding) the local configuration of the Fe ions. For example, a distorted octahedral configuration (e.g., via a rhombic field) can lead to the proper splitting of the e_g and t_g orbitals, inducing an intermediate spin state. Moving on to the 6 K spectrum of sample Fe₃O₄@LC@Dox (see Figure 5f), an additional narrow sextet (13(1) % relative spectral area) should be added to the previously discussed spectral components (81(1) % spectral area of the main broad sextet and 6(1) % spectral area of the asymmetrically split sextet). These last two components keep closely their above mentioned hyperfine parameters. The hyperfine parameters corresponding to the additional component are the following: isomer shift of 0.35(1) mm/s, quadrupole splitting of 0.10(1) mm/s, and a magnetic hyperfine field of 51.5(1) T. These parameters indicate that this additional spectral component can be attributed to Fe³⁺ ions in a high spin state with S = 5/2; however, with a slightly different electron surrounding as compared to the Fe³⁺ ions evidenced in the initial naked Fe₃O₄ MNPs. In this respect, this third sextet component with much narrower spectral lines can be easily assigned to Fe³⁺ positions in very similar configurations as well-crystallized maghemite. That is, covering Dox molecules also slightly influence the magnetic state of NPs, in addition to the stronger influence coming from the CA covering molecules (some 87% of total Fe positions are similar to the case of Fe₃O₄@LC NPs)), giving rise to additional positions (some 13% of total Fe positions), which resemble those of hematite. Given this covering molecule effect, it becomes essential to estimate the real magnetic state of the covered MNPs, and hence the corresponding magnetization of the magnetic core, before applying relation (1) for deducing the weight of the surface molecules. This will be carried out in the following section through a proper corroboration of the Mössbauer and magnetic investigations.

It is worth mentioning here on the magnetic configuration of magnetite and the specific changes induced by the cation vacancies when moving toward the maghemite structure [37,38]. In a simplistic way, the unit formula of magnetite as an inverse spinel can be written as [Fe³⁺]_T[Fe³⁺Fe²⁺]_OhO₄, with one Fe³⁺ ion (S = 5/2) with a tetrahedral (T) coordination, one Fe³⁺ ion (S = 5/2) with an octahedral coordination, and one Fe²⁺ ion (S = 2) with an octahedral (Oh) coordination. Given the ferromagnetic coupling of spins in the same atomic site type and the antiferromagnetic coupling of spins in different types of atomic sites, a total spin of S = 2 can be assigned to the formula unit (f.u.) due to the compensation of the two spins belonging to Fe³⁺ ions on tetrahedral and octahedral positions. Hence, a magnetic moment of 4 µ_B is associated with the f.u. of well-crystallized magnetite and, finally, a spontaneous magnetization of 98 emu/g, as also reported in [39]. On the other hand, maghemite can be seen as a defected magnetite structure with cation vacancies on octahedral positions and only Fe³⁺ ions. Therefore, the f.u. can be simplified according to the following expression: [Fe³⁺]_T[Fe³⁺Fe_x³⁺]_OhO₄-γ, with x = 0.66 and γ = 1. According to the above-mentioned spin coupling mechanisms, the corresponding magnetic moment per f.u. is 3.33 µ_B, to which a spontaneous magnetization of 82 emu/g can be associated (again, similar to the maximum magnetization reported in [38]). Starting from both cases of magnetite and maghemite magnetic structures, a magnetization of about 24.7 emu/g can be associated with each Bohr magneton. Under the above assumptions, the spontaneous magnetization of only 62.9 emu/g associated with the naked MNPs, where only Fe³⁺ ions (more than 98%) have been evidenced by Mössbauer spectroscopy, should infer a maghemite-like structure with a value of x lower than 0.66. A magnetic moment per f.u. of only 2.54 µ_B corresponds to a spontaneous magnetization of 62.9 emu/g, following the above assumption of 24.7 emu/g associated with each Bohr magneton. Accordingly, the value of x = 0.51 corresponds to all f.u., which are not affected by the coating molecules. On the other hand, the affinity of organic molecules is expected to increase at the most defective sites, which are the octahedrally coordinated ones. This aspect is in agreement with the above observation that Fe³⁺ ions with intermediate spin states are the six coordinated ones, e.g., in the former octahedral sites. In this context, only 7% of the total Fe ions are affected by the organic molecules (see the relative spectral area of the Mössbauer component in Figure 5e), belonging to Fe³⁺ ions with S = 3/2), which means 0.17 Fe ions from a total 2.51 Fe ions per f.u. These 0.17 ions are part of the initial 0.51 ions with octahedral coordination, which contribute to the total magnetic moment of 2.54 µ_B/f.u. of the naked Fe₃O₄ MNPs. As a consequence, the magnetic moment per f.u. in the magnetic core of the surfacted NPs can be expressed as μ = 0.17 × 3 μ_B + 0.34 × 5 μ_B = 2.21 μ_B, where a magnetic moment of 3 μ_B and, respectively, of 5 μ_B has been assigned to Fe³⁺ ions with S = 3/2 and S = 5/2. Accordingly, a spontaneous magnetization of the magnetic core, M*_S of 54.6 emu/g, can be estimated in the case of sample Fe₃O₄@LC (see Table 2). Consequently, a loading of 0.044 g of LC molecules at 1 g of Fe₃O₄@LC NPs is estimated by relation (1).

In the case of sample Fe₃O₄@LC@Dox NPs, a direct and simple estimation of the magnetic moment in the magnetic core can also be obtained from the Mössbauer investigations. These show that in addition to the Fe ions in specific positions of Fe₃O₄@LC (characterized by a magnetic moment of 2.21 μ_B/f.u. and accounted by the broad and the asymmetrical sextets), new configurations approaching the ones in well-crystallized maghemite (characterized by a magnetic moment of 3.33 μ_B/f.u. and accounted by the third narrow sextet) are induced by the presence of Dox molecules. Considering the relative contributions provided by Mössbauer spectroscopy, the overall magnetic moment per f.u. in the magnetic core of Fe₃O₄@LC@Dox can be written as follows: μ = 0.87 × 2.21 μ_B + 0.13 × 3.33 μ_B = 2.36 μ_B. Accordingly, the spontaneous magnetization of the magnetic core, M*_S of 58.3 emu/g, can be estimated in the case of sample Fe₃O₄@LC@Dox (see Table 2). A loading of 0.055 g of LC@Dox molecules at 1 g of Fe₃O₄@LC@Dox NPs are estimated by relation (1). Simply, it can be estimated that loading with Dox molecules is only 0.011 g per g of Fe₃O₄@LC@Dox NPs, which is about one order of magnitude lower than in the case of Fe₃O₄@CA@Dox NPs.

In order to compare this result with the spectrofluorimetric results on the same sample presented in [30], we should mention that the release of Dox strongly depends on the pH value of the buffer solution, with a quasi-complete release taking more than 90 h (there is high imprecision with regard to release time due to the asymptotic decrease in the Dox concentration in time). However, assuming a quasi-linear decrease in the Dox concentration in the PBS buffer solution, which extrapolates the data in Figure 8 of [30], an average release concentration per hour of about 4 µM of Dox (M = 543 g) can be assumed, together with a release time of 90 h, finally leading to about 2 µg/mL of total Dox. With the reported concentration of the NP solution (200 µg/mL), one obtains about 10 µg of Dox at 1000 µg of NPs, or equivalently, about 0.010 g of Dox at 1 g of NPs, which is in reasonable agreement with the results provided by the proposed methodology.