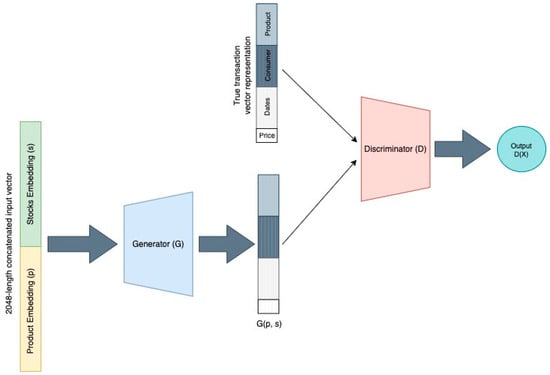
Consumer Transactions Simulation Through Generative Adversarial Networks Under Stock Constraints in Large-Scale Retail

The objective of this section is to rigorously evaluate the efficacy of the proposed GAN model in generating realistic transaction data that adheres to real-world constraints. We employ a comprehensive experimental setup, leveraging proprietary data and employing multiple performance metrics to assess the quality of the generated transactions.

4.1. Dataset

The dataset used in this research is provided by one of the largest retailers in Europe, holding a significant share of the domestic market. This unique dataset offers a rare opportunity to study consumer behavior and retail operations at scale. The data encompasses various aspects of retail transactions, including but not limited to customers, products (Product ID, Product Name, Size, and other metadata), transactional details (e.g., ID, price, quantity, date, etc.), stores (Store ID, City, and other metadata), and stocks (availability and quantity of a product per day per store).

The dataset is particularly valuable for several reasons. Its scale allows for a robust statistical analysis and the training of complex machine learning models like GANs. The diversity means it is likely to be representative of broader shopping behaviors in Europe, thereby increasing the generalizability of the research findings. The dataset includes fine-grained details, such as product embeddings, transaction dates, and unit prices, which are crucial for the nuanced understanding and modeling of consumer behavior. Sourced from an industry leader, the dataset reflects real-world retail operations, making the research findings directly applicable to practical challenges in retail management.

The data offer a broad temporal and spatial scope as they were collected from 986 distinct retail sites over 58 days, or approximately eight weeks. It encompasses an impressive 2,061,078 customers. The dataset is particularly rich in transactional data, containing 31,183,932 transactions. It records an average of approximately 3,464,881 transactions per week. This high volume of transactional data is crucial for training sophisticated machine learning models, such as the Generative Adversarial Network (GAN) model proposed in this study. Each transaction involves an average of nearly 14 products, of which around 11 are unique. This diversity is further emphasized by the fact that each customer purchases an average of approximately 106 unique products, making the dataset highly suitable for studying assortment planning. About half (1,049,775) of the repeated customers in our training dataset have engaged in transactions at multiple sites. This high customer loyalty indicates recurring purchase patterns essential for accurate demand forecasting. Moreover, the dataset includes 29,393,436 transactions involving more than two products, and 2,055,421 transactions involving at least five distinct products, in a single transaction, while the overall assortment of the retailer contains more than 55,000 unique SKUs. These statistics underscore the complexity of consumer buying behavior, which is a central focus of this research. To enhance the dataset’s reliability, pre-processing steps were applied, including the deduplication, normalization, and imputation of missing values. These steps are crucial for ensuring robust embeddings and a consistent performance during model training.

In summary, the dataset’s extensive scale, diversity, and granularity make it an exceptional resource for investigating the challenges and opportunities in retail operations, particularly in assortment planning and demand forecasting. Given its real-world relevance and the scale at which the data have been collected, the research findings are expected to have direct and significant implications for the retail industry, especially for large-scale retailers.

4.2. Model Design and Training

We experimented with various architectures and configurations of our GAN model. There are two observations worth noting, based solely on the architectural experimentation: WGAN-GP significantly increases the stability of training even in the first epochs. At the same time, slightly different architectures for Generator and Discriminator help to avoid mode collapse at the initial training stages (even when a gradient penalty is not applied). The final architecture (Figure 1) we used in this study is described below. Hyperparameter values were selected based on a grid search over learning rates, batch sizes, and hidden layer dimensions. The final configuration prioritized stability (e.g., through WGAN-GP) and performance, as shown in Figure 2.

The Generator is a neural network comprising four fully connected layers with the following dimensions:

Layer II: 1024 to 512 units, followed by a LeakyReLU activation.
Layer III: 512 to 256 units, followed by a LeakyReLU activation.
Output Layer: 256 to 1287 units, followed by a Tanh activation.

The Discriminator also consists of a neural network with three fully connected layers:

Layer I: 1287 input units to 512 output units, followed by a LeakyReLU activation and a dropout layer.
Layer II: 512 to 128 units, followed by a LeakyReLU activation and another dropout layer.
Output Layer: 128 to 1 unit, followed by a sigmoid activation.

The generator’s loss function is a weighted combination of the GAN loss and a reconstruction loss (Equation (5)). The GAN loss aims to deceive the discriminator, while the reconstruction loss ensures that the generated embeddings are close to the real product embeddings.

$L_{R} = \frac{1}{N} \sum_{i = 1}^{N} {‖e_{r e a l, i} - e_{g e n, i}‖}_{2}^{2}$

(5)

where N—number of samples, e_real_,_i—real product embedding for the ith sample, and e_gen_,_i—generated product embedding for the ith sample.

Two different optimization algorithms are employed for training the Generator and Discriminator: the Generator uses the with a learning rate of 0.0002 [40] and β values of (0.5, 0.999), and the Discriminator uses the RMSprop optimizer [41] with a learning rate of 0.0002. The Discriminator is trained five times for each Generator update. The Discriminator loss is computed using real and fake orders and a gradient penalty term to enforce the Lipschitz constraint [42].

The training process of the proposed Generative Adversarial Network (GAN) model is formalized as Algorithm 1 to provide a structured and easily interpretable overview of the vital computational steps. Although we cannot publish a full PyTorch implementation because of the proprietary nature of collaboration and data sourcing, by delineating the process in this manner, we aim to offer a transparent and replicable framework that can be readily understood and implemented by researchers and practitioners alike. The training, evaluation, and inference processes were performed using NVIDIA DGX A100 40 GB.

Algorithm 1. Training Process of the Proposed GAN Model

1: Input: Training dataset, batch size, number of epochs
2: Initialize: Generator G, Discriminator D
3: Initialize: Optimizers optimizer_G, optimizer_D
4: for epoch in 1, 2, …, epochs do
5:        for mini-batch in DataLoader do
6:              Extract real orders and stock embeddings
7:             Extract product embeddings from real orders
8:              Move all data to computation device (GPU)
9:                 for iteration in 1, 2, …, n_critic do
10:                    Generate fake orders using G
11:      Compute Discriminator loss L_D
12:      Update D using optimizer_D
13:              Generate fake orders using G
14:              Compute Generator loss L_G
15:                Update G using optimizer_G

4.3. Performance Metrics

Evaluating the performance of Generative Adversarial Networks (GANs) is challenging, especially in non-visual domains. The limitations of GANs in discriminative tasks and their sensitivity to domain shifts make the evaluation process intricate [43]. To address these challenges, we employ a multi-faceted approach to assess the quality of the generated transactions using the following metrics.

Jensen–Shannon Divergence (JSD): A symmetric measure of the similarity between two probability distributions. It is particularly useful for comparing the distributions of real and generated transactions in our context. The JSD is the average of two Kullback–Leibler divergences, one for P and one for Q, the probability distributions of real and generated transactions, respectively.

$J S D (P, Q) = \frac{1}{2} D_{K L} (P‖ M) + \frac{1}{2} D_{K L} (Q‖ M)$

(6)

where

$M = \frac{1}{2} (P + Q), D_{K L} (P‖ Q) = \sum_{x} P (x) l o g \frac{P (x)}{Q (x)}$

(7)

In retail transactions, the tail behavior of the distribution can be crucial. JSD is sensitive to differences in the tails of the distributions, making it a suitable metric for our application. A lower JSD value means that the two distributions are more similar in an information-theoretic sense.

Earth Mover’s Distance (EMD): Measures the distance between the probability distributions of real and generated transactions. Similarly to the above, a lower EMD value indicates that less “work” is required to transform one distribution into another, suggesting that the two distributions are more similar.

$E M D (P, Q) = {i n f}_{γ ϵ \prod (P, Q)} \int_{X \times Y} d (x, y) d_{γ} (x, y)$

(8)

Classification Accuracy (Acc): Utilizes a simple binary classifier to distinguish between real and fake samples in the downstream task. We follow the same approach used previously in [34] to create a classifier different from the one used to train GAN. An accuracy of around 0.5 would mean that the classifier cannot distinguish a real transaction representation from a generated one.

By employing these metrics, we aim to provide a comprehensive and robust evaluation of the quality of transactions generated by our GAN model. Each metric offers a unique perspective: EMD focuses on the overall distribution, classification accuracy provides an operational view, and JSD gives a balanced and bounded measure. It is worth highlighting that both EMD and JSD are used to measure the similarity between two probability distributions. Still, they have different properties and sensitivities that make them suitable for diverse types of analyses. EMD is useful for understanding the overall shape and spread of the distribution, including the impact of outliers, which could represent high-value transactions, while JSD compares the core behaviors of customer transactions, especially when outliers are less of a concern. Together, they allow for a nuanced understanding of the model’s performance.

4.4. Results and Discussion

In this section, we present the results of our experiments designed to evaluate the efficacy of various GAN models in generating plausible retail transactions. The models were trained using different combinations of consumer and product embeddings, with and without including stock information, including its weighting variation. Our experiments demonstrate that Cleora outperforms word2vec-based embeddings in EMD and JSD metrics, emphasizing its suitability for large-scale retail datasets.

In evaluating our GAN models, summarized in Table 1, we observed significant performance variations based on the type of embeddings and the inclusion of stock information. The EMD and JSD metrics were lower for models trained with weighted stocks, indicating a closer match to the real data distribution. Particularly, models utilizing RNN for consumer embeddings and Cleora for product embeddings achieved the best results with EMD and JSD values of 0.16 and 0.07, respectively. These models also achieved a classification accuracy closest to 0.5, which is considered ideal in the context of GANs as it signifies that the generated transactions are nearly indistinguishable from the real ones. In comparison to [33] which used LSTMs, our GAN-based approach incorporating stock constraints achieved a superior alignment with real-world distributions (lower EMD and JSD). Similarly, our method improved that of [34] by capturing assortment dynamics.

When comparing these results to models trained without stocks, the importance of incorporating stock information becomes evident. Models without stock information had higher EMD and JSD values, indicating a greater divergence from the real data distribution. Moreover, their classification accuracy was far from the ideal 0.5 mark, making them more easily distinguishable from real transactions. These findings strongly support our hypothesis that weighted stocks provide more informative embeddings, thereby enhancing the performance of GANs in generating realistic retail transactions.

Source link

Sergiy Tkachuk www.mdpi.com

Greenberg News

Consumer Transactions Simulation Through Generative Adversarial Networks Under Stock Constraints in Large-Scale Retail

4.1. Dataset

4.2. Model Design and Training

4.3. Performance Metrics

4.4. Results and Discussion

Greenberg

4.1. Dataset

4.2. Model Design and Training

4.3. Performance Metrics

4.4. Results and Discussion

Related Posts

A Qualitative Case Study from Tamil Nadu and Punjab, India

Environmental Factor – November 2021: Insight into endocrine disruptor bisphenol A advanced by NIEHS

15th IRENA Assembly to Set Energy Transition Narrative for 2025

Greenberg