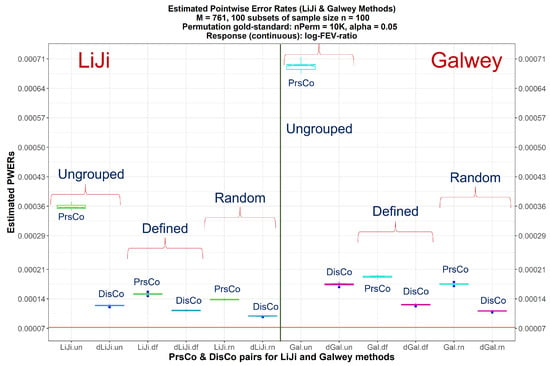
Distance-Correlation-Based p-Value Adjustment Enhances Multiple Testing Corrections for Metabolomics

Greenberg January 8, 2025 in News - 2 Minutes

We compare the performance of seven procedures to estimate M_eff, six popular in GWAS literature [26] and one recently introduced for MWAS: 1. Bonferroni [3]; 2. Šidák [4]; 3. Nyholt [22]; 4. Li and Ji [23]; 5. Gao et al. [13]; 6. Galwey [17]; and 7. Peluso et al. [10]. For the estimation of M_eff, for Bonferroni and Šidák,

M_{eff} =

M; whereas the last five procedures are based on eigen-analysis of the features’ correlation matrix. To obtain eigen-vectors, we use principal component analysis (PCA; [27,28]). PCA is a high-dimensional data analysis procedure that provides projected directions of maximum variation among a set of data points in a real coordinate space. In an M-dimensional space, the unit-length principal components (PCs; directions) are computed sequentially. That is, the m-th PC is orthogonal to all the previous

(m - 1)

PCs while explaining the maximum variability not explained by the previous PCs. Thus, PCA provides orthonormal bases with M spanning vectors projecting the original data along the directions of maximum variability. Often, researchers use PCA as a tool for reducing the dimension of the M-dimensional data to a lower-dimensional space spanned by just the first few PCs. In our context, PCA can be used on the correlation matrix (using PrsCo or DisCo) of the metabolomics features. For example, let A be an M-by-M correlation matrix of M metabolites’ abundances (log-transformed and adjusted for the clinical covariates, if applicable). Then the elements of

A = ((a_{i j})), i, j = 1, \dots, M,

will, respectively, consist of the PrsCo or the DisCo of the

i^{t h}

and the

j^{t h}

metabolites’ abundances. In the equations below,

{\hat{λ}}_{i}

are the M eigenvalues obtained from the eigen-analysis of the estimated correlation matrix, such that

{\hat{λ}}_{1} \leq {\hat{λ}}_{2} \leq {\hat{λ}}_{3} \leq \dots \leq {\hat{λ}}_{M}

. Note that, while the eigen-values obtained from the eigen-analysis of the PrsCo matrix conveniently indicate the variance explained by the corresponding eigen-vectors, the same interpretation might not necessarily hold true for the DisCo matrix. Our study objective, however, is not to intepret the variance-explaining features of the eigen-values/vectors, but, rather, to use the matrix as an intermediate step for accurately estimating the effective number of tests in a multiple testing scenario.

The five eigen-analysis-based procedures to estimate M_eff give rise to the following:

$N y h o l t : {\hat{M}}_{eff}^{N} = 1 + (M - 1) \cdot (1 - var (\hat{λ}) / M^{2});$

(4a)

$L i J i : {\hat{M}}_{eff}^{LiJi} = \sum_{i} f (| {\hat{λ}}_{i} |); where, f (x) = I (x \geq 1) + (x - ⌊ x ⌋);$

(4b)

$G a o : {\hat{M}}_{eff}^{G} = no . of PCs explaining \geq 99.5 % of total variation;$

(4c)

$G a l w e y : {\hat{M}}_{eff}^{Gw} = {(\sum_{i} \sqrt{{\hat{λ}}_{i}})}^{2} / \sum_{i} {\hat{λ}}_{i};$

(4d)

$P e l u s o : {\hat{M}}_{eff}^{P} = {(\sum_{i} \sqrt{{\hat{λ}}_{i}} / \log ({\hat{λ}}_{1}))}^{2} / (\sum_{i} {\hat{λ}}_{i} / {\hat{λ}}_{1} + \sqrt{{\hat{λ}}_{1}}) .$