1. Introduction
The effectiveness of antimicrobials for the treatment and prevention of infections is informed by preclinical and clinical studies. Clinical trials are considered the gold standard for assessing the effectiveness and safety of antimicrobials [
1,
2]. However, prior to clinical studies, adequate safety and efficacy of new compounds should be established using preclinical models [
3,
4]. Animal-based models are employed for evaluating the safety and pharmacodynamics of antimicrobials [
5,
6,
7]. These studies can measure the complex interactions between the immune system, pathogens, and antimicrobials [
8,
9]. Animal models offer an invaluable tool for the preclinical development of an antimicrobial; however, animal models have important limitations [
10,
11], including the ethical concerns regarding animal rights and welfare [
12,
13]. Moreover, the follow-up period before determining treatment outcomes (e.g., survival) in animal models does not sufficiently align with the disease process in humans [
11]. For instance, it is difficult to monitor the emergence of resistant bacteria during the course of treatment in the most commonly used rodent animal models, often due to the death of the animals [
14] and the inability to sustain the model over a clinically relevant duration. Consequently, various
in vitro infection models are used to study the effect of antimicrobial exposure on bacterial killing and the emergence of resistance for different dosing regimens and course durations.
Although the
in vitro infection models do not fully replicate the interactions of the host, antimicrobials, and microorganisms [
15,
16], they provide crucial preclinical insights into the direct actions of antimicrobials against pathogenic organisms without the involvement of the immune system. Hence,
in vitro infection models contribute significant insights for the optimisation of antimicrobial dosing regimens. These models are categorised into static and dynamic models based on whether the antimicrobial concentration remains constant or changes during the study period [
17].
In static
in vitro infection models, the pathogenic organisms are exposed to a fixed concentration of the antimicrobial/s [
18], unlike dynamic
in vitro infection models, in which the concentration of the antimicrobial/s changes during the experimental period. Hence, the dynamic
in vitro models mimic the fluctuation in antimicrobial exposure in the human body [
15,
19]. The dynamic antimicrobial exposure in dynamic
in vitro models is achieved by a controlled flow of drug-free growth media at a rate mimicking the pharmacokinetics of the antimicrobial/s [
20,
21].
The simulation of humanised pharmacokinetic profile of the antimicrobials helps to characterise their pharmacokinetic/pharmacodynamic (PK/PD) indices, which serve as surrogate indicators of efficacy in describing dose–exposure–response relationships. The common indices include the ratio of maximum concentration (C
max) to the minimum inhibitory concentration (MIC) (C
max/MIC), the fraction of dosing interval for which the free antimicrobial concentration is above the MIC (
fT
>MIC), and the ratio of the area under the curve (AUC) of concentration-vs.-time plot to the MIC (AUC/MIC) [
14,
22,
23,
24]. The determination of the PK/PD index in these models helps optimise the dose and treatment schedule of both new and commercially existing antimicrobials [
25,
26]. The optimised dose and dosing schedule of antimicrobials derived from dynamic
in vitro infection models is often predictive of clinically effective dosing regimens with a high rate of accuracy for translation into clinical settings [
27]; this is often prospectively validated in clinical studies prior to implementation in routine clinical practice [
28,
29]. Dynamic
in vitro infections models are, therefore, invaluable tools both in the development and post-marketing optimisation of antimicrobial therapy.
While there has been an increasing recognition of the utility of dynamic in vitro infection models in both academia and industry, the wider application of these models in antimicrobial optimisation is relatively limited. This is in part due the technical intricacies of the model and the lack of detailed published guidance in the model setup and pharmacokinetic simulation approaches. Therefore, the purpose of this review is to discuss the model setup, mathematical simulation approaches, and application of dynamic in vitro PK/PD infection models used in antimicrobial development and optimisation. Static in vitro infection models and dynamic flow in vitro models that do not simulate or are not commonly used to simulate humanised pharmacokinetics and animal models are beyond the scope of this review paper.
3. Simulating the Pharmacokinetics of Antimicrobials
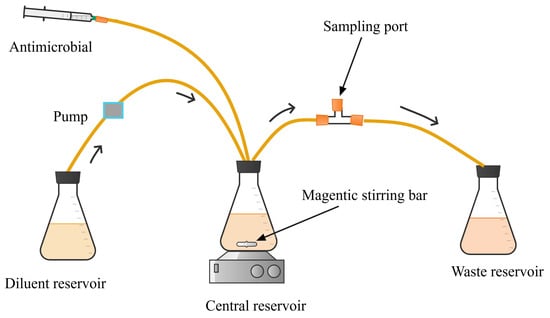
Dynamic
in vitro infection models are used to describe the time course of response to antimicrobial therapy when microorganisms are exposed to the dynamic free concentrations of the antimicrobials as they occur in the human body [
99,
112]. The pharmacokinetics (dynamic concentration–time profile) of antimicrobials in
in vitro infection systems is simulated using methods described by Blaser et al. [
113] and Kesisoglou et al. [
114]. This involves controlling the flow of drug-free media into and out of the central reservoir to mimic the elimination pharmacokinetics of antimicrobials in the human body [
115]. The models can be used to simulate the pharmacokinetics of both combination and monotherapy regimens. For monotherapy simulation, the fluid flow rates to and from the central compartment are adjusted based on the clearance of the antimicrobial being tested. One-compartment kinetics is usually simulated by calculating the “humanised clearance” of the study drug that corresponds to the volume of the distribution of the
in vitro system (which can be specified as needed, usually ranging from 100 to 500 mL) to keep the same half-life of elimination as in humans (Equation (1)).
where Cl is the humanised clearance of the antibiotic, t1/2 is the half-life, and VC is the volume of the central compartment.
When simulating the pharmacokinetics of the combination of antimicrobials with a distinct clearance or half-life, modification of the dynamic
in vitro setup (
Figure 8) is needed. The setup can be configured in either a serial or parallel manner to accommodate the distinct pharmacokinetic profiles of the drugs [
114].
The first serial setup in a dynamic infection model for two antimicrobials that differ in half-life was developed by Blaser in 1985 [
113]. In this model, the net inflow of media into the central reservoir is set based on the clearance of the antimicrobial with a shorter half-life and higher clearance rate. For instance, to simulate the pharmacokinetics of a combination of two antimicrobials, A and B, in HFIM, where the clearance of A is greater than that of B, the flow rate of the
in vitro system is adjusted according to the clearance of antimicrobial A [
113]. Since antimicrobial B is eliminated more rapidly than expected, it is supplemented into the central reservoir at a concentration equivalent to its target concentration. This is achieved by pumping antimicrobial B from the supplementary reservoir to the central compartment at a flow rate equivalent to the difference in clearance of the two antimicrobials, offsetting its excess elimination associated with the rapid clearance of the
in vitro system [
113]. To determine the dose of antimicrobial B for supplementation, the volume of its supplementary reservoir (
VB) is first determined using Equation (2) [
113].
where ClA and ClB are the clearances of antimicrobial A and B, respectively, and VC is the volume of the central compartment.
The bolus mass of antimicrobial B (
MB) injected into the central compartment is determined using Equation (3).
where CBmax and VC are the peak concentration of B and the volume of fluid, respectively, in the central compartment.
The infusion rates of antimicrobial B into the serial vessel or supplementary reservoir (
IB,S) are determined based on the infusion rate to the central compartment (
IB,C) and the volumes of the fluids in the central compartment and the supplementary reservoir (Equation (4)).
The amount of antimicrobial B (
mB) bolus injection into the supplementary reservoir within a short period is calculated as
where MB is the mass of antimicrobial B bolus injected into the central vessel, and VB and VC are the volumes of fluid in vessel B and in the central compartment, respectively.
Pharmacokinetic profiles for combinations of three or more antimicrobials, each with differing clearance or half-life, could be simulated using a serial or parallel configuration setup, as described by Kesisoglou et al. [
114]. Implementing the serial arrangement of the
in vitro system involves determining the antimicrobial flow rate and the volumes of broth in each antimicrobial-containing vessel. In a serial configuration of HFIM for three antimicrobials (
Figure 9), for instance, the antimicrobial with the highest clearance (antimicrobial A) will be bolus dosed and/or infused into the central compartment. The other antimicrobials (antimicrobials B and C) are administered (bolus or infusion) into both the central compartment and their respective serial vessels.
In serial configurations, unlike the Blaser
in vitro design from 1985 [
113] for two-antimicrobial combinations, Kesisoglou et al. [
114] made the following modifications for the combination of three or more antimicrobials.
The volume of the serial vessel or feeding vessel for N number of antimicrobials (A, B, C, …) has the flexibility of being changed if the elimination rate constant of antimicrobial A (KA) is greater than the elimination rate constant of the other combinatory antimicrobials (KB, KC, etc.) and VAKA > VBKB + VCKC + …, where KA, KB, and KC and VA, VB, and VC are the elimination rate constants and the respective volumes of the fluid containing antimicrobials A, B, and C, respectively.
The injection period for each antimicrobial in all vessels should not necessarily be large.
The series design does not necessarily require that the maximum concentration of each antimicrobial solution flowing to the central compartment from its respective supplementary reservoir is equal to its concentration in the central compartment; i.e., Ciin max ≠ Cimax for any antimicrobial i because there is a flexibility in changing the ratios of the vessel fluid volumes, where Ciin max is the maximum concentration of the antimicrobial i flowing to the central compartment, and Cimax is the maximum concentration of the same antimicrobial in the central compartment shortly after administration.
Representations of the symbols for dosing, concentrations, volumes, and the flow rates of three or more antimicrobials (A, B, C, …) in the serial HFIM of
Figure 9 are presented in
Table 2.
In the serial configuration, the dose of antimicrobial i injected into the central compartment (
Mi) and each supplementary reservoir (
mi) is determined using Equations (6) and (7).
The potential of the serial HFIM design to predict the pharmacokinetics of the combinations of levofloxacin, meropenem, and ceftazidime was experimentally validated by Kesisoglou et al. [
114]. This study revealed that the half-life and the target concentration of the studied antimicrobials were within the acceptable range of their target pharmacokinetic parameters with slight deviations [
114]. This suggests that the series HFIM design holds promise as a tool for predicting the pharmacokinetics of antimicrobial combinations
in vitro.
In the parallel configuration of HFIM (
Figure 10), the supplementary reservoir of each antimicrobial is arranged in such a way that it can feed its contents to the central reservoir. This HFIM setup involves dosing each antimicrobial i into the central compartment and the corresponding reservoir [
114]. Each antimicrobial flows into the central compartment at a rate simulating the clearance of the individual antimicrobial in the human body.
In the parallel configuration of the HFIM, the bolus dose of each antimicrobial i into the central compartment is determined by Equation (8):
where Cimax is the peak target concentration of the antimicrobial i, Ci(0) is the concentration of the antimicrobial i at time 0 if any, and VC is the total volume of the central compartment.
The amount of antimicrobial i (
mi) injected into the corresponding vessel is determined by Equation (9):
where Cimax is the peak concentration of antimicrobial i in the central compartment, Fout is the fluid flow rate from the central compartment to the waste reservoir, Ki is the fluid flow rate constant of antimicrobial i, and VC is the volume of fluid in the central compartment.
The parallel configuration of the HFIM was experimentally validated using the humanised pharmacokinetics of combinations of meropenem, ceftazidime, and ceftriaxone. The observed pharmacokinetic profile of the three antimicrobials was within the acceptable range of the target simulated profile [
116], demonstrating that the parallel HFIM configuration is a promising design for studying the pharmacokinetics of multi-drug combination regimens
in vitro.
4. Application of Dynamic In Vitro Infection Models in the Development and Optimisation of Antimicrobials
The application of dynamic
in vitro infection models in antimicrobial development has been progressively increasing in the last decade. They enable basic pharmacodynamic profiling of antimicrobials to generate key initial data that could be used as a reference for further investigation in animal model experiments and clinical trials. This reduces the unnecessary waste of time and cost required for antimicrobial research and development in clinical settings [
45,
47]. Indeed, these models have been instrumental in the development of various antimicrobials including antibacterials [
50,
117,
118], antifungals [
105], and antivirals [
119,
120,
121,
122,
123,
124]. For instance, the novel antibacterials zoliflodacin [
118] and lefamulin [
117], aimed at treating
Neisseria gonorrhoea infection, were initially evaluated in HFIM. Similarly, a dynamic
in vitro aspergillus infection model was used in the development of the new antifungal, F901318, which showed promising potential for clinical application in treating fungal infections including aspergillosis [
105].
A key application of dynamic PK/PD models in the initial stage of antimicrobial development is in elucidating the PK/PD exposure–response relationship of antimicrobials, thereby guiding the selection and optimisation of antimicrobial regimens. The
in vitro system allows full control of variables for flexibility in designing the traditional dose fractional studies used to identify the PK/PD drivers of efficacy. For example, HFIM was used for dose-fractionation studies to identify free AUC/MIC ratio as the PK/PD index of gepotidacin, a novel first-in-class antibiotic, and determine the magnitude of its PK/PD index [
125]. In this study, the free-drug AUC/MIC ratio needed to prevent resistance amplification was also determined over the treatment course, which would not be possible in the traditional animal model of infections used for fractionation studies. Another example is the novel beta-lactam/beta-lactamase inhibitor combination aztreonam/avibactam, for which the PK/PD drivers for both aztreonam and avibactam in the combination were derived using dose-fractionation data generated from the HFIM [
126]. In addition to dose-fraction studies, advanced mathematical modelling and simulation can also be applied to data generated from dynamic
in vitro PK/PD infection models to predict the PK/PD index of antimicrobials [
127,
128].
In addition to new drug development, dynamic
in vitro infection models have been used as a key tool supporting ongoing efforts to repurpose existing antimicrobials for novel indications. Nixon et al. [
129], for example, used the HFIM to evaluate the pharmacodynamics of flubendazole against
Cryptococcus neoformans in their effort toward repurposing this antiparasitic drug for the treatment of Cryptococcal Meningoencephalitis. Another example is the work of Srivastava et al. [
130], in which they used the HFIM for repurposing cefazolin, in combination with avibactam, for the treatment of drug-resistant
Mycobacterium tuberculosis (TB).
Another key application where in which dynamic
in vitro infection models have the most advantage is the development of alternative regimens for treating infections caused by drug-resistant microorganisms. For instance, HFIM has been widely used and recommended for the evaluation and development of alternative anti-tuberculosis combination regimens that provide synergistic rapid bactericidal activity while suppressing the emergence of resistance [
131]. Such hollow fibre system tuberculosis models have been shown to have a high predictive accuracy of clinical outcomes [
27]. In addition to synergistic combinations, dynamic infection models enable the optimisation of alternative modes of administration or dosing schedules that could suppress the emergence of resistance. For instance, when evaluated in HFIM, the sequential administration of sulfamethoxazole/trimethoprim, linezolid, and clindamycin resulted in suppression of the emergence of resistance in
Staphylococcus aureus more effectively [
132]. Similarly, extended and continuous infusion of aztreonam in combination with ceftazidime/avibactam showed a greater bacterial suppression effect compared with intermittent administration against
Escherichia coli and
K. pneumonia in HFIM [
133].