Representative stress–strain curves obtained in the uniaxial tensile tests are shown in Figure 4, while the main results are summarized in Table 6.

The stress–strain curves shown in Figure 4 present the typical hyperelastic behavior, characterized by an initial “toe region” in which small deformation results in a linear increase in stress, followed by a “plateau region”, where stress remains relatively constant despite further increases in strain, and, finally, a stiffening region in which the material experiences a significant increase in stress as a result of material stiffening. According to the literature [34], rubber stiffening can be attributed to two phenomena: the first is related to the achievement of the maximum extensibility of the polymeric chains during stretching, while the second mechanism regards the occurrence of strain-induced crystallization.

As the crosslinking density of natural rubber increases, the stress–strain curves in Figure 4 show a progressive stiffening of the samples. This can also be noted when comparing the stress required to deform the materials by 200% and 400% (see Table 6), the values of which increase, moving from NR_1.5S to NR_3.5S. For example, σ_400% is equal to 2.1 MPa in NR_1.5S and 8.0 MPa in NR_3.5S. This is a reasonable result considering that the chain length between crosslinks is reduced as the degree of crosslinking increases and, consequently, the limit of chain extensibility is reached earlier [35,36]. Focusing on the stress and strain at break, it is possible to observe that while σ_b is comparable among the samples, ε_b undergoes a reduction, even if not dramatic, with an increasing degree of crosslinking.

To evaluate the elastocaloric properties, the NR samples were deformed up to 500%. It is interesting to note that the stress required to achieve this deformation ranges between 3 MPa (NR_1.5S) and 15 MPa (NR_3.5S), and is close to the stress required to compress a refrigerant fluid in the current air conditioning systems, i.e., approx. 1 MPa [37]. This is a positive aspect that must be underlined since other caloric materials under study for developing solid-state refrigeration systems, such as shape memory alloys or ferroelectric materials, require stresses of at least one or two orders of magnitude higher. For example, for shape memory alloys, several hundreds of MPa are required to exhibit elastocaloric performance [8]. This makes the behavior of NR interesting and of great potential for solid-state cooling applications.

An elastocaloric cooling device requires the repetitive stretching and releasing of rubber. Consequently, it becomes crucial to thoroughly examine the mechanical response of the samples under cyclic loading conditions, particularly considering their susceptibility to the Mullins effect. Figure 5a–c shows the stress–strain response of the NR samples under cyclic tensile loading when maximum strain levels of 200%, 300% and 400% are applied.

Analyzing Figure 5a–c, the Mullins effect can be observed in all the samples, particularly in those subjected to a deformation of 300% and 400%. Progressing from the first to subsequent cycles, a noteworthy stress-softening phenomenon becomes evident, together with a reduction in the hysteresis loop, which is representative of the dissipated energy. As the deformation level increases, the prominence of the Mullins effect becomes increasingly apparent. This empirical observation aligns with existing literature on the subject [30]. However, to derive a more precise comparison among the cyclic behaviors of the samples, the stress at the maximum deformation per each cycle (peak stress) and the energy dissipated in the 1st, 2nd, 5th and 10th cycles have been determined, with the results shown in Figure 6a–c and Figure 7a–c, respectively, while the residual deformation at the end of the 10th cycle is reported in Figure 8.

Several considerations can be made. As can be seen from Figure 6, the stress-softening is more pronounced moving from the first to the second cycle. After the second cycle, the maximum stress only slightly decreases, suggesting the mechanical response of the material has stabilized. With increasing strain levels, the difference between the peak stress of the first and second cycles increases as well. The same consideration can be made also for the energy dissipated. The variation of the hysteresis loop from the first and successive cycles is even more pronounced than the stress-softening. For example, NR_2.5S experiences a reduction of dissipated energy from 0.8 J/cm³ to 0.4 J/cm³ moving from the first to the second cycle. For maximum deformation levels of 200% and 300%, the samples show quite similar dissipated energy values. In contrast, significant differences can be noticed for a deformation of 400%, in which NR_1.5S presents the highest value, followed by NR_3.5S and NR_2.5S. A larger number of dangling chains and trapped entanglements compared to the other crosslinking levels may explain the higher hysteresis found for the NR_1.5S sample [38]. Similar results were found by Quian et al. [39], who investigated the influence of filler size and crosslinking degree on the Mullins effect in filled NR/butadiene rubber (BR) blends. They observed that by keeping the filler content constant, the dissipated energy increased when reducing crosslinking density. Such a clear trend is not observable in Figure 7c, but still, NR_1.5S was shown to be the sample with the most important hysteresis. However, in the future, it will be essential to conduct further analysis to validate this hypothesis.

Finally, the residual deformation values at the end of the 10th cycle are shown in Figure 8. The values range from 2% to 6% depending on crosslinking degree and applied strain. When holding the degree of crosslinking constant, there is a rise in residual deformation with increasing strain levels. Conversely, maintaining a constant strain level, the residual deformation increases with the crosslinking density, specifically at 200% and 300% strain levels, while at 400%, the values are close to each other. Since the residual deformation was evaluated at the end of the 10th cycle, its trend as a function of cycle number is not known. However, since both dissipated energy and peak stress show the same behaviors, it could be reasonable to assume that the residual deformation does so as well. Consequently, it may be hypothesized that most of the residual deformation results from the first cycle.

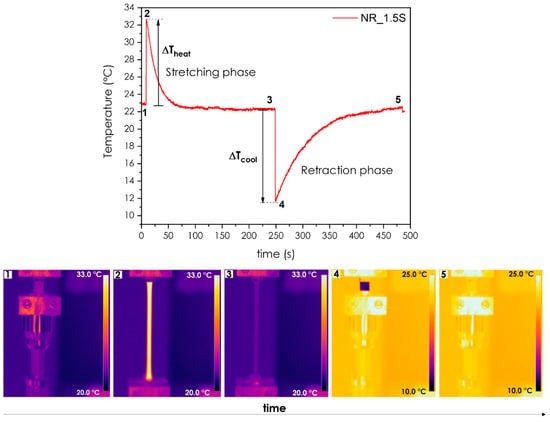
Figure 9a–c shows the temperature variation of the surface of the NR samples during the stretching and retraction phases as a function of time and deformation, while Figure 10a–e reports the most important results.

For all the samples, in all testing conditions, the elastocaloric effect is evident. The fast stretching of the material induces a positive temperature variation caused by the orientation of the macromolecules in the impact direction. When the samples are maintained in traction, the temperature progressively drops, returning to ambient temperature and reaching thermal equilibrium. In the retraction phase, the return of the material to the undeformed state, characterized by a high entropy state, causes the rubber to cool down. The deformation strongly affects the surface temperature evolution of the samples, as in all the cases the increase in strain results in a more significant temperature variation, during both the stretching and retraction phases. The higher orientation of the macromolecules achieved with increasing strain levels probably favors strain-induced crystallization phenomena. Such an effect of deformation on temperature variation is in line with the results reported by Yukihiro et al. [20,40]. The increased thermoelastic and SIC contributions are probably at the basis of this experimental observation. However, in the future, XRD analysis should be performed in situ to confirm this hypothesis.

By comparing the temperature responses of the samples in Figure 9a–c and Figure 10a–b, it is clear that the crosslinking density is another parameter that influences the thermal response of NR. Moving from Figure 9a to Figure 9c, a decreasing trend in the temperature variation of the samples can be observed. This experimental observation is probably the result of two contributions. The first is related to the limit of chain extensibility. As was previously explained, when the degree of crosslinking increases, the chain length between crosslinks is reduced and the limit of chain extensibility is reached earlier. Intuitively, this means that the entropy variation from the random coil configuration to the limit of chain extensibility is more pronounced for the rubber showing the lower crosslinking degree, since macromolecular mobility is less restricted. The second aspect concerns strain-induced crystallization. As reported in the literature, by reducing crosslinking density, the ability of natural rubber to crystallize under strain improves [34]. Thus, at a given deformation, the higher strain-induced crystallization phenomena and thermoelastic contribution make NR_1.5S the samples with the higher ΔT, during both the stretching and retraction phases. From Figure 10b, it is possible to see that NR_1.5S shows a ΔT_cool of 2.9 °C at 300% and 11.0 °C at 500%. In the literature, the highest ΔT_cool registered for NR is 12 °C [9].

For a given deformation and crosslinking degree, ΔT_cool is similar to or even larger than ΔT_heat (Figure 10a,b) in almost all the cases. Only for NR_2.5S deformed at 200% and NR_3.5S deformed at 200% and 300%, the temperature increase during stretching is larger than the temperature reduction during unloading. This is an interesting result since, in the literature, ΔT_heat is very often larger than ΔT_cool [11], suggesting non-negligible dissipative phenomena such as friction. In this work, it is plausible that during the maintenance of the samples in traction, crystalline domains progressively develop. As the crystallization of these domains is not instantaneous, the heat generated during their formation may not have been considered in ΔT_heat. Conversely, during unloading, if all crystalline domains, regardless of their formation time, melt, they could contribute to ΔT_cool, potentially resulting in ΔT_cool values greater than ΔT_heat. However, it is crucial to emphasize that this is still a hypothesis and demands further experimental investigation.

Following further analysis, it can be noted that the width of the temperature peaks in Figure 9a–c (i.e., the time required to the sample to return to ambient temperature) is wider in the retraction phase with respect to the stretching stage. The characteristic time of temperature dampening, determined during both heating (stretching phase) and cooling (retraction phase) reported in Table 7, confirms this observation.

For a given degree of crosslinking and deformation, the τ_c calculated in the retraction phase is always higher than the one calculated in the stretching phase. More specifically, the ratio between τ_c determined in the retraction phase and τ_c determined in the stretching stage ranges between 1.8 and 3.6. During stretching, the specimen becomes thinner, favoring a more rapid heat transfer. For the heat transfer coefficient, values ranging from 11 to 24 W/(m²·K) are obtained. According to the literature, typical ranges of h are 3–20 W/(m²·K) under the condition of free convection, and 10–100 W/(m²·K) under forced convection [41]. The rapid stretching and unloading of the samples might have triggered air movements, inducing a slight forced convection. Thus, it can be stated the values obtained are in line with data from the literature.

Going into details on the elastocaloric effect, Figure 10c–e show Q_ab and the COP_mat values of the samples as a function of deformation and degree of crosslinking. Since the elastocaloric effect of natural rubber is being studied for solid-state cooling applications, it is fundamental to quantify the capability of the material to extract thermal energy from the environment. For a given crosslinking density, Q_ab increases with increasing deformation, whereas, if the deformation is fixed, Q_ab decreases with the degree of crosslinking. NR_1.5S is the sample able to extract a higher amount of thermal energy during the unloading phase. In particular, at a deformation of 500% and in one loading/unloading cycle, NR_1.5S absorbs approx. 16.4 J/cm³. However, to evaluate the performance of the materials, the attention should be focused on the Coefficient of Performance, evaluated by the ratio between the extracted thermal energy and the mechanical work required to deform the samples (W, Figure 10d). The findings clearly show that NR_1.5S is the best formulation among the ones prepared, exhibiting a COP_mat ranging from 1.8 to 2.4. The optimal compromise appears to be reached by deforming NR_1.5S at 400%. This not only allows for the highest COP_mat value, but also ensures a safer operational condition, as it is further from the strain at break. The COP_mat values obtained were found to be higher than those reported by Bennacer et al., who used the same expression for calculating COP [11].

Finally, it can be interesting to make a comparison between the elastocaloric performance of shape memory alloys reported in the literature [9] and NR_1.5S, the most promising NR formulation among the ones tested. Three parameters are considered for the comparison reported in Table 8: the deformation imposed during the elastocaloric tests (Δε), ΔT_cool/Δσ where Δσ the maximum stress needed to deform the material, and ΔT/Δε.

NR exhibits a strain two orders of magnitude higher than that of shape memory alloys. NR needs to be stretched several times its original length to demonstrate noteworthy elastocaloric performance, presenting a drawback in the context of designing compact air conditioners. Consequently, the elastocaloric strength ΔT/Δε in natural rubber is two orders of magnitude lower. In the literature, a suggested approach to address this challenge is to work with pre-strained natural rubber [9]. On the other hand, the parameter ΔT_cool/Δσ is two orders of magnitude higher compared to shape memory alloys, which is an important advantage as the stress required to deform natural rubber is well below that required for metal alloys and quite close to the stresses involved in current air conditioners.