Fountain Coding Based Two-Way Relaying Cognitive Radio Networks Employing Reconfigurable Intelligent Surface and Energy Harvesting

1. Introduction

Two-way relaying

(TWR)

is an effective method for addressing key challenges in wireless networks, including reliability, spectral efficiency, and energy constraints [1,2,3]. In

TWR,

two source nodes exchange data through one common relay(s), which processes the received data and forwards the processed data to both sources. In [4,5,6], the common relays perform an XOR operation on the packets received from the two sources and then broadcast the XOR-ed packet back to them. Therefore, this scheme is known as the three-phase Digital Network Coding

(DNC)

TWR

. Moreover, the schemes introduced in [4,6] operate in cognitive radio

(CR)

environments, where the transmit power of the secondary users is limited by an interference threshold set by the primary users. In [7,8,9], the authors proposed two-phase Analogue Network Coding

(ANC)

TWR

schemes, where the common relays amplify the signals received from two sources during the first phase and then broadcast the amplified signals to both sources in the second phase. Although the

ANC

TWR

schemes achieve higher throughput than the DNC TWR ones, the sources in

ANC

TWR

must perform interference cancellation, which is too complex to implement in practice. In [10,11,12,13], joint Successive Interference Cancellation

(SIC)

and

DNC

are applied at the common relays and these

TWR

schemes also use only two phases for the data exchange. In particular, during the first phase, both sources simultaneously transmit their packets to the common relays with different transmit power levels. The common relays then perform

SIC

to decode the received packets. Finally, the relays apply

XOR

to the decoded packets and transmit the

XOR-ed

packet to both sources in the second phase. Recently, many

TWR

models utilizing new communication techniques have been developed, proposed, and analyzed. The authors in [14,15] studied the performance of the

TWR

schemes using radio-frequency energy harvesting

(EH)

, where the transmitters have to harvest energy from the radio signals of the surrounding nodes to transmit data. In [16,17,18], the TWR schemes using full-duplex

(FD)

techniques were proposed, where the source and/or relay nodes were equipped with multi-antennas. Although the

FD

TWR

schemes use only one time slot for the data exchange between two sources, they require high synchronization between all nodes as well as complex interference cancellation implementation. However, the related works in [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18] did not consider fountain coding

(FC)

, which is studied in this paper.

Fountain coding

(FC)

[19,20] can be efficiently used in wireless communication applications due to its simple implementation and environment condition adaptation ability. In fact, an

FC

source encodes its data to generate encoded packets (or

FC

packets), which are continuously sent to a destination. The destination only needs to collect a sufficient number of

FC

packets to recover the original data from the source. Another advantage of

FC

is to provide high information security. As proven in [21,22,23], if the destination receives a sufficient number of

FC

packets before the eavesdroppers, the source data will be secure. The authors in [24] proposed a cooperative transmission model that employs

FC

, non-orthogonal multiple access

(NOMA)

, cooperative jamming technique, and intelligent reflective surfaces

(IRS)

(or reconfigurable intelligent surface

(RIS)

) to enhance secrecy performance.

IRS

RIS

are flat-structured surfaces whose arrays of passive and programmable components used to reflect incoming signals to the intended receivers for enhancing the quality of the received signals [25,26]. Published works [27] evaluated secrecy performance of

IRS

-assisted wireless communication networks with presence of an eavesdropper. The authors in [28] proposed a down-link system where a multi-antenna base station uses

NOMA

to serve two users with the help of

RIS

. Additionally, both continuous and discrete phase shifting were considered in [28]. Another report [29] also considered the

IRS

-assisted wireless communication system using

NOMA

, and evaluated the performance of the proposed system in an interference-limited environment. In [30], the authors considered a multi-IRS down-link scheme utilizing wirelessly

EH

. Recently, the

TWR

schemes using

RIS

have gained much attention of researchers. In [31], the authors evaluated outage probability

(OP)

and average throughput of

IRS

-aided

TWR

schemes, where two sources communicate through the

RIS

(instead of common relays in the conventional

TWR

schemes). Reference [32] analyzed performance of

IRS

-aided

TWR

networks employing

SIC

, in terms of

OP

and ergodic rate. The authors in [33] proposed three power allocation algorithms for

RIS

-based Decode-and-forward

(DF)

TWR

models to improve the system sum rate. In [34,35],

IRS

-aided TWR networks using full-duplex techniques were proposed and analyzed. However, the published works [27,28,29,30,31,32,33,34,35] did not apply

FC

into the

RIS

-based

TWR

systems.

This paper investigates $TWR$ $CR$ schemes that incorporate $FC$ , $RIS$ , and wirelessly energy harvesting $(EH)$ . In our model, two secondary sources aim to exchange data with the help of a RIS deployed in the network. Using $FC$ , one source continuously sends $FC$ packets until the other source has collected enough to fully recover the original data. Moreover, the transmit power of each source is adjusted based on an interference constraint set by a primary user and the energy harvested from a power station. The new points and main contributions of this work are summarized as follows:

–: Firstly, this paper considers two $TWR$ schemes, i.e., conventional scheme (named Cov-Scm) and modified scheme (named Mod-Scm). The purpose of proposing the Mod-Scm scheme is to enhance the reliability of data transmission and reduce delay time, compared to the Cov-Scm.
–: Secondly, we derive closed-form expressions for $OP$ at each source, system outage probability $(SOP)$ , and average number of $FC$ packet transmissions needed for successful data exchange in the proposed schemes over Rayleigh fading channels.
–: Next, simulation results are presented to validate our analytical findings and compare the performance of the considered schemes.
–: Finally, we examine the effects of key parameters on overall performance. The results also present that the Mod-Scm scheme obtains better performance, as compared with the Cov-Scm scheme, in terms of reliability (OP, SOP) and delay time (average number of FC packet transmission).

The remaining structure of this paper is as follows: Section 2 describes the system model for the considered

TWR

CR

schemes along with operational principles. In Section 3, we compute the performance via mathematical expressions. Section 4 validates the analytical findings through simulations. Finally, Section 5 gives important conclusions and insights.

2. System Model

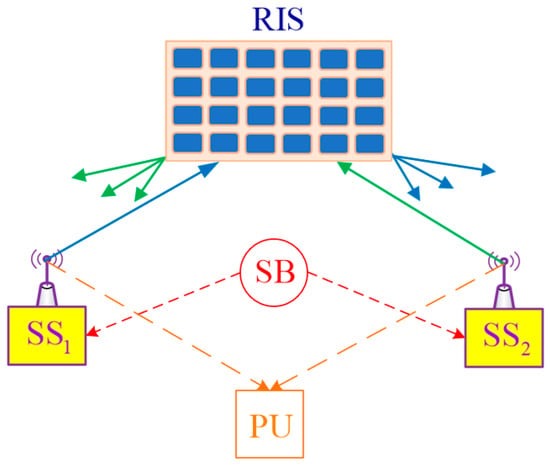
Figure 1 shows the system model of the proposed

FC

-based

TWR

CR

model, where secondary sources (

{SS}_{1}

and

{SS}_{2}

) exchange data with each other.

Let $m_{1}$ and $m_{2}$ denote the data sent by ${SS}_{1}$ and ${SS}_{2}$ , respectively. Since direct communication between ${SS}_{1}$ and ${SS}_{2}$ is outage due to their far distance, a reconfigurable intelligent surface $(RIS)$ is deployed to assist these data exchange. Let $K (K \geq 2)$ represent the number of small reflective elements in the $RIS$ . Additionally, a power beacon station (denoted by $SB$ ) is deployed in the secondary network to provide energy for ${SS}_{1}$ and ${SS}_{2}$ . To prevent co-channel interference, the frequencies used for energy harvesting differ from those used for the data transmission. The transmit power of ${SS}_{1}$ and ${SS}_{2}$ is constrained by an interference threshold established by a primary user ( $PU$ ). Assume that all channels experience block Rayleigh fading and that all devices are single-antenna nodes.

The proposed scheme can be applied to IoT networks, where ${SS}_{1}$ and ${SS}_{2}$ are IoT devices with limited power and energy. Therefore, the station power (SB) is deployed to provide energy for two source nodes. Moreover, due to spectrum scarcity, the underlay cognitive radio technique is employed for the IoT networks.

Following the operational principle of $FC,$ ${SS}_{i} (i = 1, 2)$ divides $m_{i}$ into small, equally sized packets, which are then used to create $FC$ packets. Let $p_{i}$ denote one FC packet of ${SS}_{i}$ . To successfully recover $m_{i}$ , ${SS}_{j} (j = 1, 2, j \neq i)$ must collect at least $H_{\min, i}$ packets $p_{i}$ . In addition, let $N_{\max, i}$ as the maximum number of $FC$ packets sent by ${SS}_{i} .$ For simplicity in presentation and analysis, we can assume that $H_{\min, i} = H_{\min, j} = H_{\min}$ and $N_{\max, i} = N_{\max, j} = N_{\max}$ $\forall i, j$ .

In the conventional $FC-TWRCR$ scheme $(Cov-Scm)$ , ${SS}_{1}$ continuously transmits packets $p_{1}$ to ${SS}_{2}$ through the $RIS$ . After $N_{\max}$ transmission times, ${SS}_{1}$ stops the transmission. If ${SS}_{2}$ correctly receives at least $H_{\min}$ packets $p_{1}$ , the data transmission is successful, and otherwise, ${SS}_{2}$ experiences an outage. Then, ${SS}_{2}$ in turn transmits packets $p_{2}$ to ${SS}_{1}$ through the $RIS$ , also using $N_{\max}$ transmission times. Similarly, for the successful recovery of $m_{2}$ , ${SS}_{1}$ must receive at least $H_{\min}$ packets $p_{2}$ by the end of this transmission.

In the modified $FC-TWRCR$ scheme $(Mod-Scm)$ , ${SS}_{i} (i = 1, 2)$ first transmits packets $p_{i}$ to ${SS}_{j} (j = 1, 2, j \neq i)$ . If ${SS}_{j}$ gathers enough $H_{\min}$ packets $p_{i}$ after $N_{i}$ transmission times $(N_{i} \leq N_{\max})$ , ${SS}_{j}$ sends an ACK message back to ${SS}_{i}$ . Upon receiving the ACK message, ${SS}_{i}$ ends its transmission, and ${SS}_{j}$ begins its transmission. Notably, if $N_{i} = N_{\max}$ , ${SS}_{j}$ does not need to send feedback to ${SS}_{i}$ because ${SS}_{i}$ must stop its transmission, regardless of whether ${SS}_{j}$ has received enough $H_{\min}$ packets $p_{i}$ or not. Otherwise, if $N_{i} < N_{\max}$ , the remaining transmission times $(N_{\max} - N_{i})$ can be allocated to ${SS}_{j}$ in the second transmission phase, i.e., allowing ${SS}_{j}$ to send at most $N_{\max} + (N_{\max} - N_{i})$ packets $p_{j}$ to ${SS}_{i}$ . Similarly, as soon as ${SS}_{i}$ receives enough $H_{\min}$ packets $p_{j}$ , it also sends an ACK message to inform ${SS}_{j}$ .

Remark 1.

In the

Cov-Scm

scheme [36], the data transmission of

{SS}_{1}

and

{SS}_{2}

operates independently, making the transmission order of

{SS}_{1}

and

{SS}_{2}

irrelevant. However, in the

Mod-Scm

scheme, the system performance depends on whether

{SS}_{1}

{SS}_{2}

transmits first (this issue will be examined in Section 4). Moreover, the

Cov-Scm

scheme always uses a total of

2 N_{\max}

transmission times, while the

Mod-Scm

scheme uses fewer, because the transmission stops as soon as each source gathers enough desired packets.

Let

g_{XY}

represent the channel gains between nodes X and Y, and its distribution functions expressed as

$F_{g_{XY}} (x) = 1 - \exp (- λ_{XY} x), f_{g_{XY}} (x) = λ_{XY} \exp (- λ_{XY} x),$

(1)

where $F_{g_{XY}} (.)$ and $f_{g_{XY}} (.)$ are cumulative distribution function $(CDF)$ and probability density function $(PDF)$ of $g_{XY}$ , respectively, $λ_{XY} = {(d_{XY})}^{PL}$ [36] with $PL (2 \leq PL \leq 6)$ being the path-loss factor and $d_{XY}$ being the physical distance between $X$ and $Y$ .

Let

d_{{XRIS}_{k}}

as the distance between the node

X

and the

k - th

reflector component of the

RIS

, where

k = 1, 2, \dots, K

X \in {SS}_{1}, {SS}_{2}\}

. As assumed in [37], we can assume that all the distances

d_{{XRIS}_{k}}

are identical, i.e.,

d_{{XRIS}_{k}} = d_{XRIS}

(

λ_{{XRIS}_{k}} = λ_{XRIS}

)

\forall k

Considering the transmission of a packet

p_{i}

from

{SS}_{i}

{SS}_{j}

via the

RIS

. Assume that the total delay for each transmission of

p_{i}

is normalized to 01 (time unit). During the interval

α (0 < α < 1)

{SS}_{i}

harvests energy from

SB

, and its harvested energy can be calculated as

$Q_{i} = η α P_{SB} g_{{SBSS}_{i}},$

(2)

where $η$ represents a conversion efficiency, and $P_{SB}$ is the transmit power of $SB$ .

The remaining interval

(1 - α)

is allocated for the transmission of

p_{i}

. Therefore, the average transmit power of

{SS}_{i}

can be formulated as

$P_{{SS}_{i}}^{(1)} = \frac{Q_{i}}{1 - α} = χ P_{SB} g_{{SBSS}_{i}},$

(3)

where $χ = η α / (1 - α) .$ Moreover, the transmit power of ${SS}_{i}$ must satisfy the interference threshold set by PU, i.e.,

$P_{{SS}_{i}}^{(2)} = \frac{I_{PU}}{g_{{SS}_{i} PU}},$

(4)

where $I_{PU}$ is the interference threshold.

From Equations (3) and (4), the transmit power of

{SS}_{i}

can be formulated by

$P_{{SS}_{i}} = \min (P_{{SS}_{i}}^{(1)}, P_{{SS}_{i}}^{(2)}) = \min (χ P_{SB} g_{{SBSS}_{i}}, \frac{I_{PU}}{g_{{SS}_{i} PU}}) .$

(5)

Next,

{SS}_{i}

transmits

p_{i}

{SS}_{j}

, and the received signal at

{SS}_{j}

is given as (see [38,39,40]):

$y_{{SS}_{j}} = \sqrt{P_{{SS}_{i}}} \sum_{k = 1}^{K} h_{{SS}_{i} {RIS}_{k}} r_{{RIS}_{k}} h_{{RIS}_{k} {SS}_{j}} p_{i}^{modu} + n_{{SS}_{j}},$

(6)

where $h_{{SS}_{i} {RIS}_{k}}$ and $h_{{RIS}_{k} {SS}_{j}}$ are channel coefficients of the ${SS}_{i} \to {RIS}_{k}$ and ${RIS}_{k} \to {SS}_{j}$ links, respectively, $r_{{RIS}_{k}}$ is response of the $k - th$ component of the $RIS$ , $p_{i}^{modu}$ is the modulated signals of $p_{i}$ , and $n_{{SS}_{j}}$ is zero-mean Gaussian noise at ${SS}_{j}$ . We assume that variance of all Gaussian noises is identical and equal to $σ_{0}^{2}$ , i.e., $Var \{n_{{SS}_{j}} = σ_{0}^{2}$ .

We note that

g_{{SS}_{i} {RIS}_{k}} = {|h_{{SS}_{i} {RIS}_{k}}|}^{2}

and

g_{{RIS}_{k} {SS}_{j}} = {|h_{{RIS}_{k} {SS}_{j}}|}^{2}

, where

|h_{{SS}_{i} {RIS}_{k}}|

and

|h_{{RIS}_{k} {SS}_{j}}|

are amplitude of

h_{{SS}_{i} {RIS}_{k}}

and

h_{{RIS}_{k} {SS}_{j}}

, respectively. Moreover, we can express

h_{{SS}_{i} {RIS}_{k}}

and

h_{{RIS}_{k} {SS}_{j}}

in exponential form as follows:

h_{{SS}_{i} {RIS}_{k}} = | h_{{SS}_{i} {RIS}_{k}} | \exp (- j ς_{{SS}_{i} {RIS}_{k}})

and

h_{{RIS}_{k} {SS}_{j}} = |h_{{RIS}_{k} {SS}_{j}}| \exp (- j ς_{{RIS}_{k} {SS}_{j}})

, where

ς_{{SS}_{i} {RIS}_{k}}

and

ς_{{RIS}_{k} {SS}_{j}}

are phases of

h_{{SS}_{i} {RIS}_{k}}

and

h_{{RIS}_{k} {SS}_{j}}

, respectively. Similarly to [37], we can express

r_{{RIS}_{k}}

r_{{RIS}_{k}} = \exp (j ς_{{RIS}_{k}})

, where

ς_{{RIS}_{k}}

is the phase response of

r_{{RIS}_{k}}

, which can be optimally adjusted by

ς_{{RIS}_{k}} = ς_{{SS}_{i} {RIS}_{k}} + ς_{{RIS}_{k} {SS}_{j}}

. Therefore, the maximum

SNR

obtained at

{SS}_{j}

for decoding

p_{i}

can be given as

$\begin{array}{l} γ_{{SS}_{i} {SS}_{j}} & = \frac{P_{{SS}_{i}} {|\sum_{k = 1}^{K} h_{{SS}_{i} {RIS}_{k}} r_{{RIS}_{k}} h_{{RIS}_{k} {SS}_{j}}|}^{2}}{σ_{0}^{2}} = \frac{P_{{SS}_{i}} {(\sum_{k = 1}^{K} |h_{{SS}_{i} {RIS}_{k}}| |h_{{RIS}_{k} {SS}_{j}}|)}^{2}}{σ_{0}^{2}} \\ = \frac{P_{{SS}_{i}} {(\sum_{k = 1}^{K} \sqrt{g_{{SS}_{i} {RIS}_{k}}} \sqrt{g_{{RIS}_{k} {SS}_{j}}})}^{2}}{σ_{0}^{2}} = \frac{P_{{SS}_{i}}}{σ_{0}^{2}} {(Z_{i, Sum})}^{2}, \end{array}$

(7)

where $Z_{i, Sum} = \sum_{k = 1}^{K} \sqrt{g_{{SS}_{i} {RIS}_{k}}} \sqrt{g_{{RIS}_{k} {SS}_{j}}}$ .

Using [37], we can obtain

CDF

Z_{i, Sum}

$F_{Z_{i, Sum}} (x) = \frac{1}{Γ (θ)} γ (θ, \frac{x}{ϕ}),$

(8)

where $Γ (x) = \int_{0}^{+ \infty} t^{x - 1} \exp (- t) d t$ and $γ (x, y) = \int_{0}^{y} t^{x - 1} \exp (- t) d t$ are gamma and lower incomplete gamma functions [41], respectively, and

$θ = \frac{K π^{2}}{16 - π^{2}}, ϕ = \frac{16 - π^{2}}{4 π \sqrt{λ_{{SS}_{1} RIS} λ_{{SS}_{2} RIS}}} .$

(9)

From Equations (7) and (8), we can see that

Z_{1, sum}

and

Z_{2, sum}

have the same

CDF

. Hence, we can omit the subscripts

i

and

j

, i.e.,

F_{Z_{i, Sum}} (x) = F_{Z_{j, Sum}} (x) = F_{Z_{Sum}} (x) .

Then, we can obtain

CDF

{(Z_{1, sum})}^{2}

and

{(Z_{2, sum})}^{2}

$F_{{(Z_{Sum})}^{2}} (x) = F_{Z_{Sum}} (\sqrt{x}) = \frac{1}{Γ (θ)} γ (θ, \frac{\sqrt{x}}{ϕ}) .$

(10)

Differentiating Equation (9) with respect to

x

, we obtain

PDF

Z_{1, sum}

and

Z_{2, sum}

$f_{{(Z_{Sum})}^{2}} (x) = \frac{1}{2 Γ (θ) {(ϕ)}^{θ}} x^{\frac{θ}{2} - 1} \exp (- \frac{\sqrt{x}}{ϕ}) .$

(11)

Next, setting

Y_{i} = P_{{SS}_{i}} / σ_{0}^{2}

, we see that

Y_{i}

is also a random variable whose

CDF

can be formulated as

$\begin{array}{l} F_{Y_{i}} (x) & = \Pr (\min (\frac{χ P_{SB}}{σ_{0}^{2}} g_{{SBSS}_{i}}, \frac{I_{PU}}{σ_{0}^{2} g_{{SS}_{i} PU}}) < x) \\ = 1 - \Pr (g_{{SBSS}_{i}} \geq \frac{σ_{0}^{2} x}{χ P_{SB}}) \Pr (g_{{SS}_{i} PU} < \frac{I_{PU}}{σ_{0}^{2} x}) \\ = 1 - [1 - F_{g_{{SBSS}_{i}}} (\frac{σ_{0}^{2} x}{χ P_{SB}})] F_{g_{{SS}_{i} PU}} (\frac{I_{PU}}{σ_{0}^{2} x}) . \end{array}$

(12)

Substituting Equation (1) into Equation (12), we obtain

$\begin{array}{l} F_{Y_{i}} (x) = 1 - \exp (- \frac{λ_{{SBSS}_{i}} σ_{0}^{2}}{χ P_{SB}} x) [1 - \exp (- \frac{λ_{{SS}_{i} PU} I_{PU}}{σ_{0}^{2} x})] \\ = 1 - \exp (- \frac{λ_{{SBSS}_{i}} σ_{0}^{2}}{χ P_{SB}} x) + \exp (- \frac{λ_{{SBSS}_{i}} σ_{0}^{2}}{χ P_{SB}} x - \frac{λ_{{SS}_{i} PU} I_{PU}}{σ_{0}^{2} x}) \\ = 1 - \exp (- κ_{i} x) + \exp (- κ_{i} x - \frac{μ_{i}}{x}), \end{array}$

(13)

where $κ_{i} = \frac{λ_{{SBSS}_{i}} σ_{0}^{2}}{χ P_{SB}}, μ_{i} = \frac{λ_{{SS}_{i} PU} I_{PU}}{σ_{0}^{2}}$ .

Finally, the channel capacity of the

{SS}_{i} \to RIS \to {SS}_{j}

link can be formulated as

$C_{{SS}_{i} {SS}_{j}} = (1 - α) \log_{2} (1 + γ_{{SS}_{i} {SS}_{j}}) .$

(14)

4. Simulation and Analytical Results

Section 4 validates the formulas derived in Section 3 using Monte Carlo simulations. Throughout this section, we fix positions of two sources and the

PU

node at

{SS}_{1} (0, 0)

{SS}_{2} (1, 0)

PU (0.5, - 0.75)

, and

RIS (0.5, 0.75)

, while the

SB

station is positioned at

SB (x_{SB}, 0.5)

, where

0 < x_{SB} < 1

. We also assign values to the following parameters as follows:

PL = 3

σ_{0}^{2} = 1,

H_{\min} = 5,

C_{th} = 1

, and

η = 0.5

(see Table 1). In all results, we fix

I_{PU} = 0.5 P_{SB}

, and denote the simulation and analytical results by

SIM

and

ANA

, respectively. It is noted that our derived expressions are applicable to all parameter values in practice. The reason we fix the values of these parameters is to focus on analyzing the impact of the key parameters (i.e.,

Δ (Δ = P_{SB} / σ_{0}^{2}),

α,

x_{SB},

K,

N_{\max}

) on the OP and SOP performance of the considered schemes. Next, as shown in figures below, the

SIM

and

ANA

results align closely, verifying the accuracy of our derivations.

Figure 2 illustrates the probability of the unsuccessful transmission of the packet

p_{i}

as a function of

Δ (Δ = P_{SB} / σ_{0}^{2})

in dB with

x_{SB} = 0.7

and

α = 0.35

. As seen, both

Φ_{1}

and

Φ_{2}

decrease as

Δ

increases. This is due to the fact that increasing

Δ

also increases the transmit power of

{SS}_{1}

and

{SS}_{2}

. Additionally,

Φ_{1}

and

Φ_{2}

with

K = 5

are lower than those with

K = 3

, which is due to the improved quality of the

{SS}_{i} \to {SS}_{j}

links at higher values of

K

. We also observe from Figure 2 that

Φ_{2}

is lower than

Φ_{1}

. This is because

{SS}_{2}

is closer to

SB

than

{SS}_{1}

, resulting in a higher average transmit power for

{SS}_{2}

as compared to

{SS}_{1}

Figure 3 presents

Φ_{i}

as a function of the fraction of time

(α)

allocated for the

EH

operation. The system parameters in this figure are set to

Δ = 15 (dB)

and

K = 4

. We can see that both

Φ_{1}

and

Φ_{2}

change significantly with variations in

α

. It is straightforward that with very low values of

α

, the transmit power of

{SS}_{i}

is also low, resulting in the low channel capacity and high

Φ_{i}

. However, when

α

is very high, the time allocated for the data transmission phase is reduced, which also leads to low channel capacity and high

Φ_{i}

. Therefore,

Φ_{i}

reaches its lowest value at a medium value of

α

. For example, with

x_{SB} = 0.3

Φ_{1}

and

Φ_{2}

obtain their minimum values at

α = 0.5

. In addition, the position of

SB

significantly impacts on

Φ_{1}

and

Φ_{2}

. Indeed, as shown in Figure 3, the value of

Φ_{1} (Φ_{2})

x_{SB} = 0.3

is lowest (highest) because

{SS}_{1} ({SS}_{2})

is nearest (farthest) to

SB

. When

x_{SB} = 0.65

Φ_{2}

is lower than

Φ_{1}

because

{SS}_{2}

is closer to

SB

than

{SS}_{1}

In Figure 4, we present

OP

at two sources in the

Cov-Scm

scheme as a function of

Δ

(dB) when

x_{SB} = 0.35

α = 0.5

and

N_{\max} = 6

. With

x_{SB} = 0.35

, the distance from

{SS}_{1}

SB

is shorter than that from

{SS}_{2}

SB

, resulting in

Φ_{2} < Φ_{1}

, and

OP

{SS}_{2}

is lower than that at

{SS}_{1}

. Hence, we observe from Figure 4 that the

OP

performance of

{SS}_{2}

is better than that of

{SS}_{1}

for all values of

Δ

and

K

. It is also shown that

OP

of both sources decreases when the values of

Δ

and

K

increase. Furthermore, the

OP

gap between the two sources also increases as

Δ

increases. It is worth noting that the results obtained in this figure can be used to design/optimize the OP performance. For example, with

K = 4

, the OP of both sources in the Cov-Scm is lower than 0.01 when the value of

Δ

is from 11 dB to 20 dB. In other words, the SB station can use a minimum transmit power of 11 dB to ensure that OP of both sources remains below 0.01.

Figure 5 shows

OP

at two sources in the

Mod-Scm

scheme as a function of

Δ

(dB) when

x_{SB} = 0.35

α = 0.5,

K = 3

, and

N_{\max} = 6

. Furthermore, we consider two scenarios: (i)

{SS}_{1}

transmits first (named

Mod-Scm-1

); (ii)

{SS}_{2}

transmits first (named

Mod-Scm-2

). We observe that in

Mod-Scm-1

OP

{SS}_{2}

is lower than that of

{SS}_{1}

at low and medium

Δ

values, and at high

Δ

values,

OP

{SS}_{1}

is higher. In

Mod-Scm-2

OP

{SS}_{2}

is always better than that of

{SS}_{1}

for all values of

Δ

. Moreover, the

OP

gap between the two sources in

Mod-Scm-2

is much higher than that in

Mod-Scm-1

, and

OP

{SS}_{2}

and

{SS}_{1}

Mod-Scm-2

are lowest and highest, respectively. Therefore, Figure 5 shows that

Mod-Scm-1

achieves greater performance fairness for two sources.

To determine whether

Mod-Scm-1

Mod-Scm-2

performs better, Figure 6 compares

SOP

of all the considered schemes. In this figure, the parameters are set to

x_{SB} = 0.35

α = 0.5,

K = 5

, and

N_{\max} = 6

. As shown,

Mod-Scm-1

obtains the best

SOP

performance, while that of

Cov-Scm

is worst. We also observe that

SOP

Mod-Scm-1

is much lower than those of

Mod-Scm-2

and

Cov-Scm

. Therefore, in this simulation, the source

{SS}_{1}

Mod-Scm

should be prioritized to transmit its data first.

Figure 7 presents both

OP

and

SOP

of the considered schemes as a function of

α

when

Δ =

8.5 dB,

x_{SB} = 0.35,

K = 3

, and

N_{\max} = 7

. It is noted that because SB is located at

(0.65, 0.5)

, we have

Φ_{2} < Φ_{1}

; hence, in

Cov-Scm

OP

{SS}_{1}

is lower than that of

{SS}_{2}

. As emphasized in Section 3, we can confirm from Figure 4 that

OP

{SS}_{1}

Cov-Scm

is equal to that of

{SS}_{1}

Mod-Scm-2

, and

OP

{SS}_{2}

Cov-Scm

is equal to that of

{SS}_{2}

Mod-Scm-1

. This figure also shows that there are optimal values of

α

at which

OP

of each user is lowest. For example, in

Mod-Scm-2

, the

OP

performance at

{SS}_{1}

and

{SS}_{2}

is best when

α = 0.35

and

α = 0.4

, respectively. For the

SOP

performance, we see that

Mod-Scm-2

obtains the best performance, while

Mod-Scm-1

still outperforms

Cov-Scm

. Similarly, there exists optimal values of

α

which provides the best

SOP

performance for the considered schemes. Based on the results obtained from Figure 6 and Figure 7, we can conclude that in the

Mod-Scm

scheme, if

Φ_{j} < Φ_{i}

(then

SOP

Mod-Scm- j

is lower than that of

Mod-Scm- i

), hence, the source

{SS}_{j}

should be prioritized to transmit data first. Now, let us consider examples of designing the proposed schemes. If the required quality of service (QoS) dictates that the SOP performance must be below 0.01, then, as shown in Figure 7, only the

Mod-Scm-2

scheme can satisfy this requirement. Moreover, the value of

α

must be designed within the range of 0.325 to 0.4. For another example, to determine the optimal value of

α

in the

Mod-Scm-2

scheme, we follow the following steps:

–: Step 1: As shown in Figure 7, the simulation and theoretical results of the SOP performance over a wide range of $α$ were used to confirm the existence of an optimal value of $α$ .
–: Step 2: Identifying the interval that contains the optimal value of $α$ . For example, in Figure 7, the interval of $α$ is (0.325, 0.4).
–: Step 3: Using the derived expression of SOP (i.e., Equation (27)) to search the optimal value of $α$ within the interval determined in Step 2.

Figure 8 studies the impact of the positions of the power station

(SB)

on the

OP

and

SOP

performance when

Δ =

11 dB,

α = 0.375

K = 4

, and

N_{\max} = 7

. Due to the symmetry, we can see that in

Cov-Scm

OP

{SS}_{1}

x_{SB} = a

equals to that of

{SS}_{2}

x_{SB} = 1 - a,

where

0 < a < 1

. Similarly,

OP

{SS}_{1}

Mod-Scm-1

x_{SB} = a

equals to that of

{SS}_{2}

Mod-Scm-2

x_{SB} = 1 - a

. For the

SOP

performance, we see that

SOP

Cov-Scm

is symmetrical about

x_{SB} = 0.5

, while

SOP

Mod-Scm-1

x_{SB} = a

equals to that of

Mod-Scm-2

x_{SB} = 1 - a

. Therefore, as

x_{SB} < 0.5 (x_{SB} > 0.5)

, the source

{SS}_{1} ({SS}_{2})

should be selected to transmit data first. Finally, it is worth noting from Figure 8 that the

SOP

Cov-Scm

Mod-Scm-1

, and

Mod-Scm-2

is lowest when

x_{SB} = 0.5

x_{SB} = 0.3

, and

x_{SB} = 0.7,

respectively.

In Figure 9, we present the average number of transmissions of

FC

packets for the successful data exchange between two sources in the

Mod-Scm

scheme as a function of

Δ

(dB) when

x_{SB} = 0.4

α = 0.2

, and

N_{\max} = 7

. It is worth noting that the number of transmissions in

Cov-Scm

is always

2 N_{\max}

. Figure 9 presents that the average number of transmissions in

Mod-Scm-1

and

Mod-Scm-2

decreases with the increasing of

Δ .

When the

Δ

values are high enough, the average number of transmissions in

Mod-Scm-1

and

Mod-Scm-2

will reach

2 H_{\min}

. Therefore, the proposed

Mod-Scm

scheme not only obtains a better

OP

and

SOP

performance, but also achieves a lower average number of transmissions. As shown in Figure 9, the average number of transmissions of

Mod-Scm-2

is lower than that of

Mod-Scm-1

. However, at high

Δ

regimes, the performance of

Mod-Scm-1

and

Mod-Scm-2

is almost the same. Finally, as observed, increasing the number of reflective elements in the

RIS

also reduces the average number of transmissions significantly.

Figure 10 presents the impact of

α

on the average number of transmissions of

FC

packets for the successful data exchange between two sources in the

Mod-Scm

scheme when

Δ = 8.5

dB,

K = 5

, and

N_{\max} = 7

. As seen in Figure 10, the average number of transmissions in

Mod-Scm-1

and

Mod-Scm-2

achieves the minimum value as

α = 0.5

. Moreover, the positions of the

SB

station also impacts the average number of transmissions significantly. In this figure, the average number of transmissions in

Mod-Scm-1

and

Mod-Scm-2

with

x_{SB} = 0.5

is the same, and is lowest as compared with

x_{SB} = 0.1

and

x_{SB} = 0.2

Source link

Hieu T. Nguyen www.mdpi.com

Greenberg News

Fountain Coding Based Two-Way Relaying Cognitive Radio Networks Employing Reconfigurable Intelligent Surface and Energy Harvesting

1. Introduction

2. System Model

4. Simulation and Analytical Results

Greenberg

1. Introduction

2. System Model

4. Simulation and Analytical Results

Related Posts

Environmental Factor – July 2022: Pride Month celebrated by NIEHS

Part II—Statistical Analysis and Interpretation of Tests

Environmental Factor – July 2022: Mathis named new executive officer, associate director for management

Greenberg