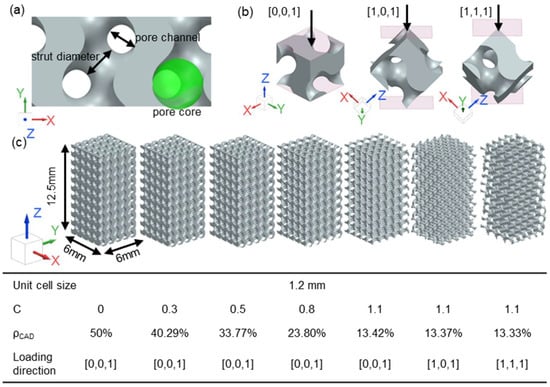
4.2. The Effect of Relative Density on Compressive Behaviours
In general, the employed LPBF process parameters ensured satisfactory manufacturing quality of the samples. The high relative densities of the struts confirm the low ratios of porosity defects. Yet, the slightly higher relative density (ρsample) observed in samples is usually characterised as overprinting, due to heat input during the process. The additional heat inevitably affects the material adjacent to the built volume. Consequently, particles may adhere to the sample surface, increasing both built volume and relative density.
The stress and strain distributions in simulations reveal the deformation behaviour of gyroid structures under compressive load. Struts in gyroid structures experience a combination of bending and compression deformation, with bending being the main cause of stress concentration and subsequent failures [
10,
28]. Stress and strain concentration predominantly occur on struts oriented at a 45° angle relative to the loading direction, corresponding to the direction of the maximum shear stress. The histograms reflect the intense stress concentrations in dense structures. Most materials experience low stresses, seen as the high-frequency peaks at lower stress ranges. In contrast, the material on 45° orientated features experiences higher stress and displays low-frequency peaks at higher stress ranges. At equal engineering strain, the stress concentration is more pronounced in dense structures, attributed to their higher stiffness. The observations suggest that increased relative density leads to greater stress concentration within the structures, which aligns with the findings reported by Yang et al. [
10]. Stress concentration approaches the yield stress of Ti6Al4V, implying the initial failure locations at stress concentrations. The thin features on the boundary surfaces of the structures caused unfavourable stress and strain concentrations. These locations are highly susceptible to initial failures, potentially leading to numerous sharp edges and ends that could pose risks in biomedical applications. Hence, implant designs should aim to minimise or avoid such thin features.
The stress–strain curves illustrate distinct deformation behaviours of gyroid structures with varying relative densities. In general, denser structures showed higher stress values due to their high stiffness. Both simulation and test curves consistently demonstrate the linear elastic sections and yield, confirming that the material model used in simulations can represent the linear elastic deformation and yield of LPBF-manufactured Ti6Al4V. However, the maximum deformation in simulations is restricted to strain = 2.5% due to software limits, resulting in the exclusion of plateau regions in the simulation curves. Discrepancies between simulation and test curves can be attributed to using a simplified material model in simulations. Furthermore, the wide plateau regions in tests consist of stress peaks and valleys over a large strain range, resulting from local collapse and regained support during continuous deformation. The periodic changes of stress over deformation align with the observation by Fan et al. [
29]. This implies the good deformability of gyroid structures during progressive failures, aligning well with their application as energy absorbers.
The deformation behaviours and failure modes of gyroid structures are strongly influenced by relative density. In the structures loaded in the [0,0,1] direction, stress typically concentrates at thin features or sharp corners. Due to the period geometry of gyroid structures, its cross-section reaches the minimum area at 45° with respect to the loading direction [
29], corresponding to a weak orientation prone to failures primarily induced by the shear load [
30]. The failure manifests as bending, plastic deformation, and fractures of the struts. The relatively thicker features in dense structures enhance local stiffness, enabling the failure and defect accumulations near initial cracks. The high stiffness also ensures that the resilient volume can support the fragments during progressive failure, seen as fragments of dense structures that horizontally shifted after initial fractures. Thus, the dense structures showed 45° diagonal fractures. Conversely, the low stiffness associated with thin struts in porous structures results in localised failure initiation. Throughout the compression tests, the low stiffness of the material cannot horizontally shift the fragments. Thus, the deformed volume in porous structures tends to stack vertically, causing layer-by-layer failures and gradual densifications.
The power relationships of Young’s modulus and yield stress show notable consistency between simulation and test results, affirming the robustness of both approaches. The slight difference can be attributed to inherent manufacturing defects within the LPBF process and the slight increase in dimensions and relative density of specimens. Transitioning to a comparison with existing literature, divergence from the power relationships proposed by Gibson–Ashby [
18] is understandable, given their use of metallic foam, a porous material distinct from the skeletal gyroid structure. Larger disparities with the work of Yan et al. [
20] can be attributed to their focus on more porous gyroid structures with a narrow relative density range (5% to 15%). This limitation can narrow the applicability of formulas that are intended to describe mechanical properties across the entire relative density range.
The power relationships of Young’s modulus and yield stress offer high customisability in various applications. By selecting appropriate C values corresponding to the desired relative density, gyroid structures with precise Young’s modulus can be accurately generated. This variability highlights the excellent potential of gyroid structures in biomedical implants, where stiffness can be tailored to align with the value of human bone (typically around 20 GPa or lower [
31]). As demonstrated in [
32], low-stiffness porous materials can be used to replace the volume of stiff metal stem components in artificial joints, thereby reducing the overall stiffness of the stem and allowing the bone to be stimulated to maintain its integrity. Based on the results of this study, gyroid structures with C = 0 achieves a stiffness of approximately 20 GPa. This geometric configuration presents a promising solution for reducing the stress-shielding effect. Similar adaptive mechanical properties are observed in various porous materials, which further explores the range of porous materials for biomedical applications [
33].
4.3. The Effect of Loading Direction on Compressive Behaviour and Anisotropy
The stress distribution of gyroid structures reflects the loading conditions of the struts. In lattice structures, the struts aligned with the loading direction primarily experience compression during deformation while lateral struts undergo stretching [
34]. By using the approach proposed by Yang et al. [
19], gyroid structures can be simplified as scaffolds of cylindrical struts, allowing for the computational determination of strut orientations using line beam data. The unique shapes of gyroid lattice structures result in struts orienting across a wide spectrum of angles, see
Figure 9. Therefore, struts experience a combination of bending and compression due to this diverse range of orientations. Comparisons of stress distribution (
Figure 5e) reveal significant stress concentration in structures loaded in the [1,0,1] and [1,1,1] directions. In the stress range over 1000 MPa and the strain range higher than 0.01, the structures loaded in the [1,1,1] direction consistently display the highest concentration, followed by the structures loaded in the [1,0,1] direction and [0,0,1] direction. Young’s modulus in the simulation results of these three structures follows the same sequence (
Table 3). This correspondence between stress concentration and stiffness is consistent with the findings from numerical analysis of the structures loaded in the [0,0,1] direction, indicating that stiffer structures demonstrate more pronounced stress concentrations under uniform compressive strain.
The mechanical response of gyroid structures changes with loading directions due to the varied strut orientations and distinct load transfer modes. Under compression, the load traverses through the lattice geometry towards the bottom of the structures, with the efficiency of this transfer influenced by the structure’s geometry and strut orientation. Cuadrado et al. [
35] compared the mechanical properties of lattice structures with different unit cells. Their results showed that as the inclination angle between struts and the loading direction increases, the deformation mechanism transfers from compression-dominant to bending-dominant, consequently reducing mechanical properties. The comparison of strut orientation in gyroid structures (
Figure 9) reveals that struts in the structures loaded in the [0,0,1] direction are aligned at larger angles with the loading direction, indicating more bending-dominant behaviour. When the structure is loaded in the [1,0,1] direction, some struts align closely with the loading direction, thereby enhancing the stiffness. However, most struts remain inclined, which restricts the stiffness. Compared to the other two directions, the [1,1,1] direction exhibits the greatest number of struts closely aligned with the compression direction. As a result, the deformation mechanism approximates a compression-dominant behaviour, leading to the highest observed stiffness in the simulation results. This direction-specific stiffness underscores the inherent anisotropy of gyroid structures.
The stress–strain curves also elucidate the influence of loading directions on the mechanical response of gyroid structures. Structures loaded in the [1,0,1] and [0,0,1] directions exhibit increased stiffness and a decreased strain at initial fractures during testing. In these structures, local stress reaches the yield point at a lower strain. In the subsequent plastic deformation, defects such as dislocations, micro-cracks, and grain boundary separations rapidly accumulate at significant strain concentration locations, leading to fractures at lower strains. The increased stiffness observed in these two loading directions is accompanied by corresponding low strain at initial fractures. However, their superior deformability remains unaffected, as evidenced by wide plateau regions and comparable absorbed energy.
The mechanical properties of lattice structures are also highly dependent on the manufacturing process. The broad range of strut orientations presents challenges to the LPBF process. Overhangs can occur when struts align more closely with the build plate. Without a sufficient solid substrate, the new layer of materials in the overhang regions is prone to increased spattering. This results in less solid deposition, increasing defects such as material loss and high surface roughness [
36]. Kranz et al. [
37] discovered that struts more parallel to the build plate tend to induce defects such as high surface roughness and dimensional inaccuracies. Shange et al. [
38] reported increased porosity when features align more closely with the build plates. These defects ultimately compromise the mechanical properties, reducing stiffness and deformability. Therefore, the support ratio of the LPBF process, defined as the proportion of the material layer supported by the previous layer, could indicate manufacturing quality.
Figure 10 compares the material layers for manufacturing gyroid structures in three loading directions, revealing significant differences in sequential layer shapes for the three loading directions, associated with different support ratios. To further quantify the support ratios, the CAD models of the structures, oriented in three loading directions, were sectioned using the layer height of the LPBF process. These section images were then compared to calculate support ratios between layers; see
Figure 11. Notably, the 2D geometries of the slices used in this analysis are identical to those used in generating laser trajectories.
The Young’s modulus in compression tests exhibited higher values than those from the simulation results (
Table 3). This increase can be attributed to the slightly higher relative densities (overbuild) of the produced gyroid structures (see
Figure 8). Despite the consistent power relationships of Young’s modulus in tests and simulations, discrepancies emerge for different loading directions. Structures loaded in the [1,0,1] direction demonstrate significantly higher stiffness in tests than the other two loading directions, which can be attributed to the improved manufacturing quality.
Figure 11c illustrates the support ratios of the material layers when structures are produced and loaded in three directions. Among these, the [1,0,1] direction exhibits the highest support ratio. Consequently, this direction is expected to have the fewest overhangs and thus the least manufacturing defects. This results in an improved load-bearing capacity for this loading direction, leading to a higher Young’s modulus. In contrast, the relatively low support ratios in the other two directions increase manufacturing defects and reduce Young’s modulus, as evidenced in
Table 3. Defects, such as porosity, can be significantly reduced by optimising laser parameters and scan strategies in the LPBF process, including adjustments to laser power and scan strategy, as demonstrated in a previous work of the authors [
39].
The failure modes of gyroid structures under the three loading directions correspond to the stress concentrations observed in simulations. The initial failure locations of structures align with the strain concentration, specifically in the middle of struts where stress and strain concentrations are highest. The struts that align more closely with the loading direction, particularly in the [1,0,1] and [1,1,1] directions, exhibit a compression-dominant deformation. However, given the wide range of strut orientations, most struts display a bending-dominant deformation mechanism. The primary failure mode in gyroid structures involves the bending and rotation of struts, indicating a bending-dominant behaviour. During the progressive failure, deformed and failed struts stacked together due to the low stiffness of the porous structures (with a relative density of around 15%) were unable to support the resilient volume.
The loading direction-dependent mechanical properties confirm the anisotropy of gyroid structures and expand the design possibilities for tailoring these structures to specific applications. In instances where a structure meets geometric parameter requirements, such as pore sizes, but requires increased stiffness, optimising the orientation of the gyroid structure can be an effective design strategy. Moreover, the flexibility and potential of gyroid structures can be significantly enhanced when integrated with a graded structure design. The radial gradient design, as demonstrated in [
21], is a promising approach to expanding the design possibilities of graded structures for enhancing mechanical performance and biological integration. For orthopaedic implants, the surface of an implant can be substituted with finely tuned gyroid structures exhibiting non-uniform stiffness and pore size. Consequently, the stress distribution at the bone interface can be customised to more effectively mitigate the stress-shielding effect, and the osseointegration process can be improved by applying an appropriate pore size.