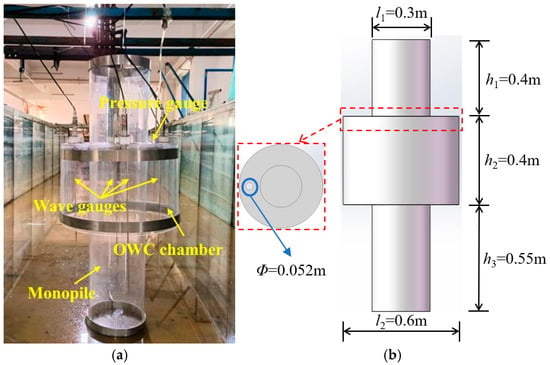
1. Introduction
Marine renewable energy is playing an increasingly significant role in ecological conservation and the development of low-carbon economies. Wave energy, characterized by its global distribution, abundant reserves, and ease of utilization, is currently the most widely applied and promising form of marine energy [
1]. Based on energy conversion principles, wave energy systems can be categorized into oscillating water column (OWC), overtopping, and oscillating body types [
2]. The OWC device features a simple structure, excellent corrosion resistance, and ease of maintenance. The overtopping device can convert unstable wave energy into stable potential energy of the water, enabling a steady and continuous energy output. The key characteristic of the oscillating body device is that the moving body is in direct contact with the waves, enabling more efficient conversion of wave energy into mechanical energy. Due to the immaturity of the technology, wave energy devices still face high levelized costs of electricity (LCOEs), thus hindering full commercialization. Among these technologies, OWC devices stand out for their simplicity and reliability: the only moving part, the air turbine, is located above the water, making it resistant to corrosion and easy to maintain [
3]. Several demonstration plants, such as the Mutriku plant, Yongsoo OWC, and OE Buoy, have already been successfully operating [
4,
5], showcasing the great feasibility and potential of OWC technology.
To harness more wave energy, researchers have optimized the conversion performance of OWC devices through experimental and numerical studies. Elhanafi and Kim [
6] investigated the performance of a 3D offshore OWC device in experiments and found that the device achieved a higher capture width ratio under long waves with low-power take-off (PTO) damping. Kharati and Fathi [
7] compared the effects of various chamber lengths and bottom slope angles on the efficiency of an OWC device. The device reached optimal efficiency with a low chamber length and a high bottom slope angle. Yamac and Koca [
8] developed a computational fluid dynamics (CFD) numerical model for an OWC device and compared the effects of coastal structures on its output power. The results indicated that the OWC exhibited the best performance when the coast had a convex arc geometry. Trivedi et al. [
9] studied the performance of the LIMPET OWC and analyzed the impact of energy dissipation on the hydrodynamic performance by presenting velocity vectors and streamlines during the fluctuation cycle. He et al. [
10] employed the particle image velocimetry technique to report the flow field characteristics around an OWC device, exploring the relationship between energy dissipation and vortex formation. Mayon et al. [
11] proposed an OWC system incorporating a cylindrical OWC and a parabolic wave reflector. This novel design significantly enhanced the energy capture efficiency and bandwidth of the device. Wang et al. [
12] established a numerical model of a dual-chamber OWC with a pitching mid-wall and investigated the effects of the chamber breadth, mid-wall position, and draft on the device performance. M’zoughi et al. [
13] presented an airflow control method for OWCs based on artificial neural networks. The control strategy demonstrated good performance and prevented the stalling behavior of the turbine. Liu et al. [
14] proposed a novel speed-amplified flux switching linear generator and improved the conversion efficiency of the wave energy converter by 13.4% [
14]. Compared to single-chamber OWCs, multiple-chamber OWCs demonstrate higher pneumatic efficiency due to reduced internal fluid sloshing [
15]. Wang et al. [
16] analyzed the differences between a five-unit OWC array and individual devices, finding that transverse spacing between units helps to mitigate destructive interactions and improves conversion performance.
In order to enhance commercial competitiveness, wave energy devices can be developed in combination with offshore structures such as marine platforms and breakwaters, which can help to reduce construction costs [
17,
18]. Naty et al. [
19] studied the feasibility of installing wave energy devices within breakwaters. The optimized configuration reduced the reflection coefficient of the breakwater and enhanced its capture efficiency. Das et al. [
20] proposed a novel concept of coupling an OWC device integrated with an overtopping device in breakwaters and evaluated the feasibility of its implementation in harbors. Xu and Huang [
21] experimentally investigated the hydrodynamic characteristics of an OWC device coupled with pile breakwaters, finding that this configuration is beneficial for structural safety and coastal protection. Howe and Nader [
22] compared the conversion performance of an OWC device when installed independently and when integrated with breakwaters. Ashlin et al. [
23] tested the performance of array OWCs integrated with offshore detached breakwaters and found that the optimal performance is achieved when the spacing between the units is three times the model width. Zhao et al. [
24] examined hydrodynamic coefficients for multi-chamber OWC breakwaters and concluded that the triple-chamber system performs better than conventional pontoon breakwaters. Zheng et al. [
25,
26] combined OWC devices with coastal structures and improved the hydrodynamic efficiency by optimizing the air chamber radius, wall thickness, and submergence. Vipin et al. [
27] investigated the performance of a breakwater-integrated OWC device in irregular waves. The parameters of the device were optimized by using a multilayer perceptron model and tree ensemble model. Wave energy devices can also be integrated with floating breakwaters, where this coupling not only enhances wave energy extraction but also contributes to the stability of the floating structure [
28,
29].
In recent years, hybrid wind–wave energy systems have gained attention due to their potential to fully utilize marine energy and share infrastructure, electrical equipment, and cabling costs [
30]. Sarmiento et al. [
31] coupled a floating semisubmersible structure with three OWC units and investigated the impact of different chamber opening configurations on platform response. Abbaspour and Farshforoush [
32] introduced a hybrid energy harvesting platform combining a wind turbine with an OWC platform, finding that the total wave energy collection output increased sixteen times compared to isolated units. Lee et al. [
33] numerically studied the performance of OWC devices integrated with jacket-type infrastructures for wind turbines and analyzed the effects of the geometrical parameters on the pneumatic power. Michele et al. [
34] developed a numerical model based on linearized theory for an OWC-integrated wind turbine system. The effects of the skirt and internal radius dimensions on wave energy conversion were studied. Using linear potential flow theory, Zhou et al. [
35] established a time-domain model for an OWC integrated into an offshore wind turbine monopole. The results showed that the introduction of the OWC reduced the horizontal and overturning moments on the monopile, thus enhancing the stability of the foundation structure. Cong et al. [
36] coupled four OWC sub-chambers into a monopile wind turbine and found that the wave forces acting on the OWC and the monopile can balance each other under certain wave conditions.
From the literature review, integrating OWC devices with offshore wind turbines has emerged as a key direction in wave energy development. However, most of the previous studies have primarily focused on the effects of OWC dimensions on energy output and structural loads. The flow characteristics and vortex development at critical locations between the air chamber and the wind turbine foundation, which are crucial for understanding the energy capture mechanisms of hybrid wind–wave systems, remain to be further investigated. In this study, a numerical model of an OWC installed in a monopile foundation for an offshore wind turbine is developed based on CFD tools. The numerical results are validated by corresponding experimental tests. The effects of wave period, chamber diameter, chamber draft, and PTO damping on energy harvesting performance are analyzed. The flow characteristics around the key component are described. The main contribution of this work is to provide a deeper understanding of the energy capture process of the hybrid system, which will be helpful in optimizing the design of the device.
The rest of the paper is organized as follows.
Section 2 illustrates the experimental setup and the numerical model.
Section 3 presents the convergence analysis and the validation of the numerical model. The effects of the key parameters and wave conditions on the hydrodynamic behavior of the hybrid system are discussed in
Section 4. Finally, the conclusions are summarized in
Section 5.
4. Results and Discussion
In this section, the flow characteristics of the hybrid OWC–wind device during the energy capture process are analyzed. The effects of key geometrical parameters including the OWC chamber diameter, chamber draft, and PTO damping on the hydrodynamic performance are discussed. In addition, the operating performance under irregular waves, which more accurately represent real sea states, is evaluated.
4.1. Effect of Chamber Diameter
Diameter is a significant factor in determining the performance of a cylindrical OWC. In this section, five different OWC chamber diameters are considered, i.e., l2 = 0.45 m, 0.525 m, 0.6 m, 0.75 m, and 0.9 m. The dimensionless ratio of the chamber diameter to the monopile diameter l2/l1 with values of 1.5, 1.75, 2.0, 2.5, and 3.0 are used for comparison. The dimensionless chamber draft and PTO damping are fixed at d/h = 0.15 and α = 1%, respectively.
The flow characteristics and vortex development at specific locations of the hybrid OWC–wind device during a wave cycle are depicted in
Figure 7. The typical case of
H = 0.1m,
λ/
l1 = 12.0, and
l2/
l1 = 2.0 is selected, and the wave direction is from left to right. At the moment of
T/4 in
Figure 7a, the OWC device reaches its peak exhalation time, during which the airflow velocity attains its maximum value. It can be observed that vortices are generated at the lower lips of the chamber. This is mainly because water particles cannot enter the cylinder chamber horizontally along the wave propagation direction but need to inflate around the edge of the air chamber. At the same time, the PTO damping restricts the motion of the free surface, leading to localized water compression below the orifice. This creates inconsistencies in the velocity and direction of water movement at various locations, resulting in the formation of vortices at both the front and back lips, which also causes energy dissipation.
At the moment of 2
T/4 in
Figure 7b, the airflow velocity is close to zero as the device is transitioning from exhalation to inhalation. The free surface elevation on the leeward side of the air chamber is higher than that on the windward side due to the disturbance effect of the monopile. The airflow velocity reaches its maximum value during the inhalation phase at 3
T/4, as shown in
Figure 7c. The velocity of the water particles below the orifice increases significantly, with the high-velocity regions mainly distributed at the lower lips of the chamber and near the free surface. At the moment of
T in
Figure 7d, the device is in the transition phase from inhalation to exhalation, and the airflow velocity approaches zero again. The free surface inside the chamber is at the lowest position, and the exchange of water with the external flow field is minimal. Consequently, both the intensity and the influence scope of the vortex are not significant.
The effects of the chamber diameter on the flow characteristics of the hybrid device are plotted in
Figure 8. The typical moment of
t =
T/4 is presented. In general, as the OWC chamber diameter increases, the distribution range of the high-velocity region for water particles inside the air chamber expands, especially on the leeward side. Furthermore, the velocity of the particles at the lower lip of the chamber increases with the chamber diameter, enabling more water to enter the chamber. In addition, vortices are formed at the inlet of the chamber, and the influence range of the vortex increases as the diameter increases, leading to more energy dissipation.
Figure 9 shows the effect of the chamber diameter on the hydrodynamic performance of the hybrid OWC–wind device. Evidently, both the free surface elevation and air pressure decrease as the chamber diameter increases. This is attributed to the more intense free surface fluctuations inside the chamber at larger diameters, resulting in higher energy dissipation, as demonstrated in
Figure 8. The
CWR of the device is presented in
Figure 9c. Although the free surface elevation and air pressure decrease with increasing diameter, the OWC with a larger chamber has a greater free surface area, which enhances the airflow generated during the energy conversion process, ultimately leading to a higher
CWR. The maximum
CWR is observed at 0.466 when the relative diameter
l2/
l1 = 0.3.
The above results suggest that the hybrid OWC–wind device performs better with a larger chamber diameter. However, for practical applications, the diameter of the OWC device should also be determined based on the engineering requirements and the load capacity of the monopile. A larger-diameter OWC chamber may be selected as long as the safety conditions are met.
4.2. Effect of Chamber Draft
This section investigates the effects of the chamber draft on the hydrodynamic performance of the hybrid device. Five chamber drafts of d = 0.075 m, 0.1125 m, 0.15 m, 0.1875 m, and 0.225 m were selected, corresponding to relative chamber drafts of d/h = 0.1, 0.15, 0.2, 0.25, and 0.3, respectively. The chamber diameter of l2/l1 = 3.0 was chosen based on the results from the last section, and the dimensionless PTO damping was set to α = 1%.
Figure 10 illustrates the flow characteristics around the device under the influence of the chamber draft.
Figure 10a indicates that, when the draft is small, waves can enter the chamber more easily and no significant vortices or energy loss occur at the lip of the chamber. However, a large difference in free surface elevation is observed around the monopile, with the free surface fluctuating more intensely, which negatively affects the energy capture of the device. As the draft increases, see
Figure 10b–e, the waves are hindered from entering the chamber and vortices are formed at the front lip. Meanwhile, the fluctuation of the free surface inside the chamber gradually decreases. Furthermore, since the wave energy is mainly concentrated at the surface, an excessively deep chamber is detrimental to wave energy capture.
The effect of the chamber draft on the hydrodynamic performance is presented in
Figure 11. Generally, the free surface elevation decreases as the chamber draft increases because the waves are obstructed from entering the chamber at larger drafts, which is consistent with the trend observed in
Figure 10. Regarding the air pressure, the amplitude values are closer under the two smaller-wave-length conditions. As the chamber draft increases, the air pressure rises and then decreases, with a sharp drop observed at the relative draft of
d/
h = 0.3. As for the CWR in
Figure 11c, it can be concluded that the chamber draft has a significant impact on the performance of the hybrid device. An appropriate draft can effectively improve the energy capture performance of the device. When the relative draft
d/
h = 0.15, the OWC achieves the maximum CWR at 0.466. Additionally, the hybrid device is sensitive to the wave length, and the optimal performance is observed at a relative wave length of
λ/
l1 = 12.0.
4.3. Effect of PTO Damping
In this section, the effects of PTO damping on energy capture performance are investigated. In the research models, the relative chamber diameter and the chamber draft were selected in terms of the above optimal studies, with l2/l1 = 3.0 and d/h = 0.15, respectively. The hybrid OWC–wind models equipped with five different PTO dampings were studied. The PTO damping is expressed by α, i.e., the ratio of the orifice opening area to the water column area, and α = 0.5%, 0.75%, 1.0%, 1.25%, and 1.5%, respectively.
Figure 12 presents the flow characteristics of the device under the effects of PTO dampings. Evidently, when the orifice opening is small (see
Figure 12a,b), the free surface elevation inside the air chamber is lower due to the significant PTO damping, which restricts the oscillation of the water. At the same time, the free surface fluctuations become more pronounced with larger PTO damping. As the orifice opening increases, see
Figure 12c–e, the damping effect diminishes and the velocity of the water particles inside the chamber increases, which leads to a higher free surface elevation. Additionally, in the case of small damping, the airflow is more easily expelled from the chamber.
Figure 13 shows the hydrodynamic performance of the hybrid device at different PTO damping levels. From
Figure 13a,b, the PTO damping effect gradually decreases as the orifice opening increases, enabling the air inside the chamber to more easily exchange with the external environment, which leads to a decrease in the air pressure inside the chamber and consequently an increase in the free surface elevation. Since the air power is the product of the pressure and airflow rate and the variations in these two parameters with respect to PTO damping are opposite, there theoretically exists an optimal PTO damping that maximizes the air power. The CWR is shown in
Figure 13c. Except for the relative incident wave length
λ/
l1 = 14.0, the optimal CWR occurs at
α = 0.75%, with a corresponding maximum value of 0.492.
4.4. Performance Evaluation in Irregular Waves
To further evaluate the operating performance of the hybrid OWC–wind device under real sea states, irregular waves were employed for the calculations in this section. The device dimensions were selected according to the optimal values derived from the above results, i.e., a relative diameter l2/l1 = 3.0, a relative chamber draft d/h = 0.15, and an orifice opening ratio α = 0.75%. The irregular wave scenarios were generated based on the JONSWAP spectrum with the peak enhancement factor of γ = 3.3. A significant wave height of HS = 0.1 m and five significant wave periods of TS = 1.27 s, 1.45 s, 1.63 s, and 1.83 s were considered.
The flow characteristics and vortex development of the hybrid device at four typical instants in an irregular wave cycle are presented in
Figure 14, with the case of
HS = 0.1 m and
TS = 1.83 s selected. The device reaches its exhalation peak at
t = 44.84 s, as shown in
Figure 14a. The free surface on the windward side remains relatively stable, while significant fluctuations occur on the leeward side due to the influence of the monopile. At this moment, vortices are observed at the entrance of the front wall. At
t = 45.43 s in
Figure 14b, the air velocity at the orifice is close to zero as the device enters the reversing phase. The flow characteristics are similar to those observed under regular wave conditions. In
Figure 14c, the device reaches its inhalation peak and significant fluctuations in the free surface are observed on both the windward and leeward sides. In addition, the velocity of the water particles on the windward side increases significantly due to aerodynamic effects. At
t = 46.45 s in
Figure 14d, the air velocity returns to zero again, and the free surface elevation inside the chamber reaches its lowest position.
The spectra of the free surface elevation and air pressure inside the chamber, obtained using the fast Fourier transform (FFT) method, are illustrated in
Figure 15. The frequency-domain results of the spectral analysis were derived from the transformation of the time-domain data, i.e., the time series of the parameter in irregular waves. As shown in
Figure 15a, both the spectral moment and peak of the free surface elevation increase with the significant period as more wave energy enters the air chamber during longer periods. Furthermore, a second-order spectral peak is observed when
TS = 1.27 s, which may be attributed to the more intense interaction between the waves and the device during shorter wave periods, leading to significant free surface fluctuations inside the chamber. The air pressure spectrum is shown in
Figure 15b, and the maximum spectral peak occurs at
TS = 1.63 s, indicating that the air pressure inside the chamber is higher at this condition.
Figure 16 presents the pneumatic power output and the CWR of the hybrid device in irregular waves. Both the power output and CWR show a trend of first increasing and then decreasing with the significant wave period, reaching a peak at
TS = 1.63 s. The peak pneumatic power output and CWR are 3.07 W and 0.47, respectively. These results reveal that the hybrid device exhibits more pronounced resonance effects with the irregular wave scenario at the specific period. Therefore, the device could be optimally designed based on the dominant wave conditions to capture more wave energy.
5. Conclusions
In this paper, the hydrodynamic performance of a hybrid OWC–wind device was investigated. A CFD numerical model was established and validated by the corresponding experimental results. The flow characteristics and vortex development around the hybrid device were presented. The effects of geometrical parameters, such as chamber diameter, chamber draft, and PTO damping, on the energy capture performance were discussed. Variations in terms of free surface elevation, air pressure, and CWR were evaluated under both regular and irregular wave conditions.
The results indicate that the hybrid device performs better with a larger OWC chamber diameter. The velocity of the water particles at the front lip increases with the chamber diameter, leading to more intense fluctuations of the free surface, which result in higher energy dissipation. The relative diameter is recommended to be l2/l1 = 0.3. Secondly, the chamber draft has a significant influence on the energy capture. When the draft is small, a large difference in free surface elevation is observed around the monopole. The hydrodynamic performance exhibits a trend of first increasing and then decreasing as the draft increases, with the optimal relative wave draft found at d/h = 0.15. The variations in free surface elevation and air pressure are oppositely influenced by PTO damping. When the PTO damping is too small, the airflow is restricted, leading to a decrease in energy capture. Conversely, when the PTO damping is too large, the air pressure inside the chamber becomes insufficient, resulting in lower performance. The peak CWR is observed with an orifice opening ratio of α = 0.75%. In addition, the hybrid device is sensitive to wave length. Under the optimal geometrical configurations, the device achieves a maximum CWR of 0.49 in regular waves and 0.47 in irregular waves.
This paper provides a foundational reference for the design of the hybrid OWC–wind device. However, the present study ignores the interactions between the air chamber and the air turbine. In future work, a numerical model that integrates the air chamber, a real air turbine, and a generator should be developed to enhance the wave-to-wire performance. Moreover, as ocean energy development extends to deeper seas, the hydrodynamic performance of wave energy devices integrated with floating wind turbines shall be further investigated.