1. Introduction
Non-destructive testing is becoming more and more increasingly applied not only in traditional and industrial solutions [
1,
2,
3,
4], but also in the search for new, alternative methods of testing material properties [
5,
6]. The rise of this type of testing saves time and reduces maintenance costs. A method that enables the examination of materials with ferromagnetic properties is the Magnetic Barkhausen Noise (MBN) method [
7,
8]. The MBN method is sensitive in changes in the magnetic domain structure of a ferromagnetic material [
9]. During the process of reorganization of the magnetic domain structure, there is a non-continuous movement of the domain walls as the magnetic domains vectors are rotating to match the direction of the magnetic field strength vector, reflected by rapid changes in the magnetization state. This causes a voltage to be induced in the measuring coil placed close to the surface of the examined material, which is called the Magnetic Barkhausen Noise. The MBN method makes it possible to detect stress [
10,
11,
12,
13,
14], fatigue changes, and microstructural changes [
15,
16] as well as study material properties [
17,
18,
19,
20,
21]. The method enables the study of material property homogeneity and directionality, which enables the detection and analysis of the anisotropy of material properties [
22,
23,
24,
25]. Anisotropy can be introduced because of exploitational changes in the material structure (e.g., directional stresses) or as a result of special manufacturing operations and the introduction of the desired characteristics of the material properties. Such properties are exemplary and possessed by specific types of electrical steel sheets. Generally, the two types can be distinguished: non-grain-oriented (NGO) and grain-oriented (GO) electrical steel [
26]. NGO steels are widely used for the production of electric motors, generators and high-speed permanent magnet synchronous machines [
27]. GO electrical steels are used in the production of transformers and non-rotating electrical devices [
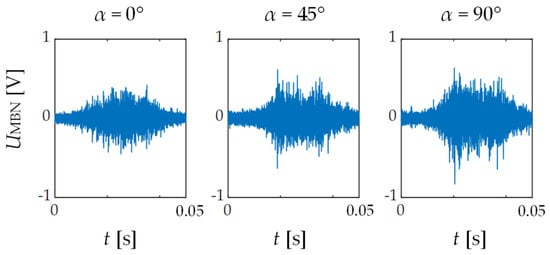
28], and these sheets have magnetic anisotropic properties. GO electrical sheets present as conventional (CGO) and with high magnetic permeability (HGO). In addition, these sheets can be subjected to various surface engineering methods that improve the magnetic parameters of the material through, for example, laser scribing. The MBN signal obtained from a material with such properties takes on the character of transitional phases (present in
Figure 1) between successive Barkhausen effect activity stages occurring in the material and therefore requires advanced signal analysis methods sensitive enough to register those phases and enable quantitative assessment. Exemplary MBN signals registered for different magnetic directions (ascribed with different α angles) of GO steel are presented in
Figure 1. One can clearly see much higher activity in terms of Barkhausen jump amplitudes and their intensity sub-periods for an easy magnetic axis (α = 90°) than for the other two.
Currently, with the increase in computing capabilities of computers, signal analysis methods using time–frequency or time-scale representations are becoming more common [
29,
30,
31,
32]. The use of time–frequency and time-scale representations to analyze the MBN signal has grown rapidly in recent years and has significantly enhanced the depth of understanding of the phenomena occurring in the process of reorientation of the magnetic domain structure during the magnetization process [
23,
24,
25,
33,
34]. So far, various transformation methods have been used for MBN data, such as the time-scale wavelet or bilinear Wigner–Ville transform [
34,
35,
36]. A detailed discussion on the transformation methods for MBN analysis was presented by the authors in [
34,
35]. One of the frequently applied methods that stands out for its potential in the analysis of stochastic MBN signals is short-time Fourier Transform (STFT). The major strength of STFT is the possibility to adjust the computational parameters for transformation operation to obtain a specific spectrogram character and resolution enabling further analysis in different ways. One of the computational parameters is the window, which slides throughout the signal, enabling frequency analysis of the signal bands for a specific time step. The type and size of the window can be adjusted. As the window size changes, the resolution in the time and frequency changes. The larger the window, the higher the resolution in frequency and the lower the resolution in time, and correspondingly, the smaller the window, the lower the resolution in the frequency and the higher the resolution in time as presented in
Figure 2. These properties play a critical role in the adjustment of the transformation results to the physical nature of MBN signals. The course of the Barkhausen phenomenon is complex, it can have local areas of increase and decrease in intensity (higher and lower MBN activity), and these phases can be associated with different aspects of structural changes in the material. Therefore, it can be considered holistically and locally. In each of these cases, there is a need to match the appropriate resolution in time and frequency, which enables using STFT. Articles [
24,
25] present various ways of transformed signal analysis using different computational window configurations. When sub-periods of MBN burst are to be analyzed and the visibility of changes in TF space is important, a smaller window can be selected, as shown in article [
25]. On the other hand, when a generalized and comprehensive analysis of the changes occurring in the spectrogram needs to be carried out, a larger [
24] window can be chosen. This enables analyzing the hidden diagnostic information of MBN from various points of view and gaining knowledge about the different properties of materials.
However, the greatest challenge arises in the proper interpretation of information encoded in a stochastic and non-deterministic signal such as MBN. In general, two approaches can be distinguished in the field of signal analysis and knowledge building from MBN signals. The first one, the most frequently used, is based on classical signal analysis and determination of signal features, often statistical ones, which are calculated from various representations of the signal, such as time, frequency, time–frequency or time-scale and the relationships between features distribution for various materials stages are analyzed [
37]. Such an approach was presented in [
38], where the MBN was observed for plastically deformed structural steel samples and statistical features were extracted from the time–frequency representations of the MBN signals. In this case, the features were plotted as a function of tension and adequate conclusions were drawn from the analysis. Another method of performing the analysis and interpretation of information is to use artificial intelligence (AI). There are two possibilities for accomplishing this approach at this point. Shallow neural networks and machine learning methods can be applied, or deep neural networks can be employed for analysis. In the case of the first approach, the calculated statistical features are provided as input parameters to a machine learning algorithm or a shallow neural network and then a classification or regression model is trained. This approach was used for the analysis of MBN signals acquired during the testing of electrical steel sheets [
39]. The second group refers to utilization of deep neural networks. Recently, AI models in the form of 1-D or 2-D convolutional neural networks (CNN) were used to more accurately analyze the information contained in the MBN raw signal or their time–frequency representations. The idea of this method refers to the calculation of features by appropriate network maps/filters and to the adaptation of the corresponding ones to the received input data. Article [
23] presents the architecture of a 2-D CNN network that was prepared to recognize changes in MBN spectrograms obtained for grain-oriented electrical steel sheets and classify them considering their properties and state. An analysis of the accuracy of the neural network in recognizing different types of grain-oriented electrical steel sheets including conventional and high magnetic permeability and additionally subjected to various surface engineering methods was undertaken. In [
40], the 1-D CNN network based on the ResNet-18 CNN (a residual network) was used for classification of sheet-metal blanking processes. Furthermore, paper [
41] employs a 1-D CNN with an inception module named InceptionTime to classify MBN signals obtained from materials with different hardness levels.
The enormous possibilities and exceptional efficiency of deep learning methods result in an increasingly growing area of their application, including the analysis of MBN signals as well. The accuracy of analysis methods using various deep structures has recently been presented in several articles. Comparison of the effectiveness of methods based on the classical approach with deep methods also indicates a higher accuracy of solving complex diagnostic problems of the latter ones. However, just as in the case of classical methods, the problem is the selection of the right set of signal features and training the method or finding the appropriate multi-parametric connection; in the case of deep learning methods, attention should be paid to the issue of data preprocessing. The question arises about the proper resolution of data used as input data for the network. Therefore, while previous studies have focused on testing the applicability of deep learning techniques in MBN signal analysis, there is a gap in understanding how specific computational parameters of time–frequency transformation affect the deep network model performance. Therefore, this article investigates the impact of window size changes on the classification accuracy by a 2-D CNN network. In the following sections, we present the 2-D CNN architecture used as a tool to examine the effect of window size on accuracy.
2. Experimental Setup
The experiment was carried out for GO electrical steel sheets. The parameters of the utilized steels are shown in
Table 1.
As can be seen (
Table 1), the specimens made from GO electrical steel sheets are of different types and are subjected to different surface engineering methods. The conventional (ascribed as C
XX#Y) and high-magnetic-permeability (ascribed as H
XX#Y) GO electrical steel samples were examined during measurement. The electrical sheets came from two different manufacturers: the samples made of steel from the first manufacturer were marked as #1 and those from the second manufacturer were marked as #2. Selected steel sheets were subjected to a laser scribing procedure (ascribed as C
XXLS#Y or H
XXLS#Y). In addition, the sheets from manufacturer #2 were subjected to removal of the coating oxide layer (ascribed as C
27P#2) and, after removal, to the application of a nitriding process (ascribed as C
27N#2). Full details of the samples involved in the experiment and the nitriding procedures, together with metallographic tests, are described in detail in the previous article [
23].
Measurements were taken with an angular resolution (α
res) of 3.6°, between 0° (TD direction of the steel) and 90° (RD direction of the steel) degrees, as shown in
Figure 3. To perform the measurement, a system consisting of a measuring transducer, a unit for analogue signal processing, a Data Acquisition Board (DAQ) and a PC computer was used. The applied excitation signal
UE had a frequency of 10 Hz and a sinusoidal shape. Due to the increasing dynamics of the magnetization process with frequency, the MBN activity identified both time and frequency increases, and so does the power spectral density increases, which cause a superposition of the periods of the high Barkhausen effect activity. However, taking into account the possibility of distinguishing these periods in time, based on preliminary tests carried out in the previous paper [
25], a frequency of 10 Hz was determined for further studies, which enabled obtaining a spectrogram characteristic that highlights all the phases occurring during the magnetization of electrical sheet metal as was discussed in previous work. The magnetic field strength generated by the measuring transducer was approximately 1.6 kA/m.
The Barkhausen effect can be observed in the range from 1 kHz to several hundred kHz. The filters in the analogue signal processing unit were adjusted during measurement [
24]. Due to the much lower energy of the components originating from the Barkhausen effect compared to the response from the excitation field, low frequencies (within the range up to several tens of Hz) need to be filtered out from the observed band of the useful signal. Furthermore, during the analysis of magnetic anisotropy properties in electrical sheets [
24], it was noted that the cutoff frequency must be adjusted to the size of the computational cell in the frequency domain resolution of the time–frequency transformation. Therefore, first, a 2 kHz high-pass filter is used to eliminate the excitation field component of the measured signal, as well as low-frequency disturbances of the measurement equipment. The upper passband range takes into account the low activity of the Barkhausen effect observed in the frequency range above 70 kHz and the Nyquist criterion and anti-aliasing filtering process related to the sampling rate (given below) as well. Thus, as a result, the signal passing to the DAQ was in the frequency range from 2 kHz to 100 kHz. The signal was read out using an NI-USB 6251 DAQ at a sampling rate of 250 kHz and stored on a PC disk managed by LabVIEW application. For one angular transducer position, 10 measurements were performed. From each measurement, 10 MBN bursts were extracted. A schematic of the measurement system is shown in
Figure 4.
In the next step, the acquired MBN signals were transformed to the time–frequency space using STFT. A window with the Kaiser function of different sizes was used for the calculations:
where I0 is the Bessel function of zero order and β is its parameter, n is a given sample and N is the size of the window w. The Kaiser function is characterized by the ability to adjust the width of the main lobe and the attenuation of the side lobes (parameter β equal 0.5 in this case), which enables it to be adapted to the specific requirements of the analysis. The window is close to the spheroidal window, which maximizes the ratio of the energy of the main lobe to the energy of the side lobes, resulting in reduced spectral leakage and improved spectral resolution [42]. A discussion on the choice of window function was given in previous article [38].
3. The Preparation of MBN Databases Used to Perform the Analysis of Time–Frequency Window Size on CNN Accuracy
Two major sets of data consisting of appropriately computed spectrograms were prepared for the experiment. Each database was developed with the same proportions: 80% training set, 10% validation set, and 10% testing set. Each of the databases contained 260 classes, which refers to 26 classes (26 transducer angular positions over the sample surface) for each out of the 10 samples tested. The first type of database consisted of four individual sub-databases, each obtained from processing the MBN signal with STFT using a different window size (128, 256, 512, 1024). In addition, windowing overlap options of 75% were used and enabled increasing resolution in time [
38]. The effective resolution values of the spectrograms obtained using STFT over time and frequency are shown in
Table 2. Considering the magnetizing field frequency of 10 Hz, a single MBN burst covers a period corresponding to 50 ms. On this basis, it can be seen that the greatest generalization of the characteristic in time can be obtained for a window of 1024 and in the frequency for a window of 128. The essence of the experiments is therefore to compare whether the generalization process taking place for different window sizes during the calculation of spectrograms leads to significant distortions of the key information on the state of the material contained in the spectrograms. Example spectrogram results obtained using different window sizes for a selected sample and different transducer angular alignments in relation to the rolling direction are shown in
Figure 5 and
Figure 6. In
Figure 5, the influence of the change in the magnetization angle and the observation of the Barkhausen effect in relation to the steel rolling direction can be seen. It can be seen that the smallest activity is visible when the transducer is oriented in the TD direction (0°) and with the rotation to the RD direction, the MBN energy clearly increases (as a result of a larger number of 180 domains in the RD direction). However, already for directions convergent with the TD angle, one can notice visible spatialization of MBN activity in time and frequency. The first region is visible for approximately 15 ms, and the second between 30 and 40 ms. With the increase in the measuring angle, another region becomes visible between the two mentioned above. Shifts in time and increases in energy of the mentioned regions are clearly visible, depending on the measurement angle.
Furthermore, from the spectrogram computational point of view, the smaller the resolution in time, the greater the energy accumulated in a smaller number of cells, which causes a higher energy value visible in the spectrogram in a single cell. Conversely, if the resolution increases, the energy is distributed over a larger number of cells. Nevertheless, the influence of the window width on the obtained representations can be clearly observed, while it is still possible to observe local MBN activities even for the extreme case of the window width.
The spectrograms that were obtained using various window sizes had different resolutions on the time and frequency axes. Thus, in order to perform the experiments using them by a single neural network, all had to be fitted to the same dimensions of 145 × 94 (this size was applied in the previous article [
23]). The process was required to train all data on a single specific artificial neural network architecture and compare the obtained accuracies. The exemplary spectrograms before and after the interpolation process are shown in
Figure 5. Each of prepared databases contained 20,800 records in the training set, 2600 records in the validation set and 2600 in the testing set as well. The second type of database that was used during the experiments combined all sub-databases (all spectrograms obtained for the four window sizes), consisting of a total of 83,200 records in the training set and 10,400 in each of the validation and testing sets.
The first type of database was applied to conduct an experiment in which the CNN training process was realized independently for data generated with a specific window size. The purpose of this experiment was to assess the impact of window size on the training process and to determine whether alternative processing could enhance classification accuracy. This approach was driven by the observation that adjusting the window size could reveal certain signal details. Additionally, this database enabled examining whether similar information patterns were present across certain window sizes. The second database was created from all data stored in independent sub-databases. The reason for this experiment was to see how well the CNN could generalize information across the entire dataset in the database, and to verify whether there was a difference in performance when checking with individual databases, each containing specific window sizes.
5. Results and Discussion
In the first experiment, three CNNs were trained using databases of the first type, i.e., four separate databases consisting of spectrograms obtained for different window sizes. Once the CNNs were trained, they were tested using a test dataset (each network individually) and then the average accuracy value was calculated.
Table 5 collects the averaged accuracy results for each network evaluated on each database.
Figure 7 is a graphic interpretation of the results shown in
Table 5.
As can be seen, the differences obtained in relation to the absolute accuracy values are definitely low. Nevertheless, the highest overall accuracy value was achieved for data processed with a window size of 256. The lowest accuracy value was obtained for data processed using a window size of 1024. The difference in accuracy values between the results obtained using the window of size 256 and 1024 is 1.53%. When testing with data created using a window other than the data the network was trained on, the highest accuracy was achieved for the network trained on data generated using a window of 128 and then tested on data generated using a window of 256. Nevertheless, a similar pattern can be observed in all analyzed cases. The second-highest score in terms of accuracy was achieved by testing spectrograms generated using a window one size larger than the base size. This is probably related to the proximity of the spectrogram’s distributions achieved for both sizes, as well as the fact that a larger window size does not cause further generalization of information (simplification of characteristics). The absolute smallest change in window size occurs between sizes 128 and 256, which likely explains the highest testing performance at a window of 256 for networks trained for a data size of 128. Taking a further perspective on the generalization of the input data by a given network, considering a quantitative description made by means of a mean accuracy value, a network trained on data using a window of 256 is able to obtain the highest rate. However, it should be noted that the differences achieved between the classes are small and do not enable an unambiguous assessment.
Another experiment was then performed in which three CNNs were trained using a second major database, which contains the spectrograms generated with all four window sizes (combining all sub-databases). The trained networks were tested on both sets of databases (individual ones and combined one) and the results of the average performance are summarized in
Table 6.
As can be seen, for a test set containing data produced with all window sizes, an accuracy of 70.06% was achieved. Again, the differences in the accuracies obtained during testing with individual databases are small. The lowest accuracy value was obtained for the test set made with a window size of 1024. The highest accuracy was obtained for the database made using a window size of 256. One can clearly see a higher value for the middle sizes. This should be referred to the relation of durations: period and window width. The windows move over the signal in the time domain pixel by pixel, but the result refers to activity over the entire interval specified by the window size. The small size results in high detail in the obtained spectrograms, while at the same time, in the lower energy value for individual cells (pixels) in the resulting image (spectrogram). The larger the size, the higher the degree of energy accumulation, but the lower the detail, the lower the distinguishability of different material states. Nevertheless, it can be noted that regardless of the size of the deep network model used, when it is trained with all data types, it is able to effectively obtain information from spectrograms. The window width of the time–frequency transformation should be understood as an element defining the level of synthesis of the encoded information. The change in resolution over time, defined by the window width, influences the simplification of the resulting image (spectrogram). As long as some limit value of the window width is not exceeded, which would cause the loss of visibility of one specific period of MBN activity on the spectrogram (high MBN energy area; see
Figure 5), this information will be possible to read and thus the deep network would be capable of extracting even subtle changes in achieved distributions. The given observation is reflected in the work by relatively similar values of the accuracy of the conducted assessment regardless of the window sizes used. This confirms the importance of deep network analysis in comparison to precise window size estimation.