Improving Resistive Heating, Electrical and Thermal Properties of Graphene-Based Poly(Vinylidene Fluoride) Nanocomposites by Controlled 3D Printing

2.1. Materials and Nanocomposite Preparation

Homopolymer grade poly(vinylidene fluoride) (PVDF) Kynar^® 721 (powder form) by Arkema (Philadelphia, PA, USA), with MFR 15 g/10 min (230 °C, 3.8 kg), a melting point of 168 °C, and a glass transition (T_g) of −40 °C was used. Graphene nanoplatelets, with grade SE1233 (GNP), a purity ≥ 97%, a tap density < 0.1 g/cm³, an average diameter D50 ~35–50 μm, and SSA (BET) 400–600 m²/g were supplied by Sixth Element Material Technology Co. Ltd. (Changzhou, China).

The GNP/PVDF nanocomposite of 6 wt% filler content was prepared by the melt extrusion process. The filler content was selected above the electrical percolation threshold (EPT) in order to obtain a printable highly conductive nanocomposite. Our previous study determined the EPT of ~2 wt% [31]. The polymer and the filler were dried at 80 °C for 4 h in a vacuum oven; then, the PVDF powder was wrapped with the appropriate amount of GNP in a ball mill for 2 h at a speed of 70 rpm. Then, the wrapped powder was extruded in a twin-screw extruder Teach-Line ZK25T (COLLIN Lab & Pilot Solutions GmbH, Maitenbeth, Germany) at temperatures of 160–175 °C and a screw speed of 60 rpm. The developed nanocomposite filament was cut in pellets and further used for 3D printing of the test samples.

2.3. Characterization Methods

Scanning electron microscopy (SEM) was performed to visualize the orientation of layers in the 3D-printed structures. Samples were cut longitudinally in liquid nitrogen and then gold-coated. SEM images of the cross-section were taken at 15 kV accelerating voltage and 110 mA emission current conditions with Tabletop SEM HIROX SH 4000 (Hirox Europe, Limonest, France) at different magnifications.

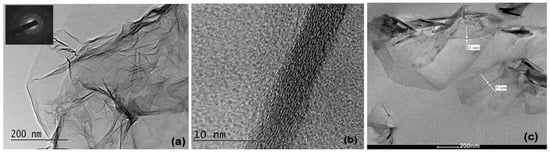
A transmission electron microscopy (TEM) analysis was performed by HR STEM JEOL JEM 2100 (Tokyo, Japan) with high-resolution operation with an acceleration voltage of 200 kV. The preparation of graphene samples was carried out by ultrasonic dispersion of GNP powder in ethanol. Then, a small quantity of the dispersion was placed on standard copper TEM meshes coated with an amorphous carbon membrane and dried at room temperature in a dust-free atmosphere. For the nanocomposite samples, thin sections were cut at room temperature with an ultra-microtome and placed on 400-mesh copper grids. The GNP sheets and the nanocomposite samples were examined at different magnifications to study the hierarchy of their structure from the micro- to nanoscale level.

Thermal analyses were performed to study the heat flow (DSC) and weight change (TGA) in the samples as a function of temperature under a controlled nitrogen atmosphere. A differential scanning calorimeter, DSC-Q20 (TA Instruments, New Castle, DE, USA), was used to monitor the heat effects associated with phase transitions of the polymer as a function of temperature in two heating runs, from 25 °C to 200 °C, at a heating rate of 10 °C/min, with subsequent cooling. From the DSC thermograms, the melting point (T_m), melt crystallization temperature (T_c), and endothermic melting enthalpy (ΔH_m) were evaluated. The degree of crystallinity (%χ_c) was calculated by Equation (1):

$χ c (%) = \frac{Δ H_{m}}{ω \cdot Δ H_{m o}} * 100$

(1)

where ΔH_m is the fusion/melting enthalpy (J/g), ω is the actual portion of polymer in the nanocomposite, and ΔH_m₀ = 104.7 J/g is the melting enthalpy for a 100% crystalline PVDF [32].

A thermo-gravimetric analysis was performed with TGA-Q50 (TA Instruments, USA) by heating from 25 to 800 °C with a ramp-up of 10 °C/min, under nitrogen flow. TG and DTG curves of weight loss and its first derivative were plotted versus temperature. Characteristic temperatures, such as the onset temperature at the start of weight loss (T_onset) and the decomposition peak temperature (T_peak), were evaluated.

Electrical resistance (R) at a room temperature of 25 °C was tested by multimeter Keithley 6517B (Keithley Instruments, Cleveland, OH, USA) using the R-mode test. Before the tests, electrical contacts of silver paint, approximately 50 μm thick, were deposited on the upper and lower surface of the sample’s short ends, to ensure Ohmic contacts with the measuring electrodes. Commercial electrically conductive adhesive LOCTITE 3850 (produced by Henkel) with a volume resistivity of 0.00001 Ω·m was used for metallization. In the presence of metallization with silver, the contact resistance was considered negligible because it was much lower (of an order of mΩ) than the measured electrical resistance of the samples (of an order of Ω), as suggested and adopted in other studies in the literature [38]. The dimension of the test section ~20 × 10 × 2 mm³ was measured for each sample by a digital micrometer with an accuracy of 0.001 mm. Three samples were electrically characterized for each raster angle, and the average values were reported with a standard error of around ±10%.

The Joule heating (resistive heating) test was performed by an experimental setup consisting of a power supply (GW Instek, New Taipei City, Taiwan) providing the voltage (V) and measuring the current (I), while the heating temperature was controlled by a thermocouple type K connected to Keithley 6517B (Keithley Instruments, USA). Similarly to the upper test for the resistance measurements, electrical contacts of silver paint were realized on the short sides of the sample and connected to the power supply. The 3D-printed samples with the raster angles of 0°, 45°, and 90° were tested, with the test section of dimension ~20 × 10 mm² and thicknesses of 0.8 and 2 mm, measured for each sample. Applying voltage to the sample, the local temperature evolution over time was measured by the thermocouple positioned at the center of the sample surface, ensuring close physical proximity to the surface by attaching it with a thermally conductive but electrically insulating LiPOLY AT910 tape (Taoyuan City, Taiwan). The goal was to have thermal coupling for accurate temperature readings without affecting the electrical measurements. Precautions were taken to ensure that no part of the thermocouple came into direct electrical contact with the sample to avoid interference with the current flowing through the sample during heating measurements. Data for the applied voltage and measured temperature, current, and time during four heating and cooling cycles were collected and recorded by the LabView Community edition software. Three samples were tested for each raster angle, and the average values were reported.

Thermo-resistive property characterization was performed, as the resistance was measured by a multimeter Keithley 6517B (Keithley Instruments, USA), while the sample was heated up on a Peltier heating plate of the AR G2 rheometer (TA Instruments, USA) from 25 °C to 160 °C. The controllable temperature was set by the AR G2 (Trios software) with a step of 20 °C and recorded by the thermocouple type K to the Keithley 6517B instrument placed in the middle of the sample. Three samples were tested for each raster angle, and the average values were reported.

The thermal conductivity of the 3D-printed samples was tested with the Laser Flash Technique (LFA 467 Hyper flash, Neztsch, Hanau, Germany) in the temperature range of 25–110 °C, as limited from the heat deflection temperature of the PVDF (HDT ~110 °C at 264 psi, according to the TDS of the producer). Sample with a size of 10 mm × 10 mm and a thickness of 2 mm, printed with the three different raster angles, were tested with the heat flow perpendicular to the printing layers. The measurements were carried out in a standard sample holder (10 mm square) with three tests for each raster angle. The results report the average values. Prior to the measurements, the front and back sides of the samples were coated with graphite to enhance the emission/absorption properties of the samples. The specific heat was determined by the reference method. Therefore, the LFA was calibrated with a C^p-standard (Pyroceram: Ø 10 mm, thickness 2 mm). The sample density at room temperature was measured using the buoyancy flotation method. From the resulting temperature excursion of the rear face measured with an infrared detector, thermal diffusivity and specific heat were both determined. Combining these thermophysical properties with the density value, the thermal conductivity was determined by Equation (2), as follows:

$λ (T) = α (T) * C_{p} (T) * D (T)$

(2)

where λ is the thermal conductivity [Wm⁻¹ K⁻¹], α is the thermal diffusivity November, Cp is the specific heat [JK⁻¹⋅kg⁻¹], and D is the bulk density [g·cm⁻³] of the composite. The Proteus^® Professional 8.6 software was used for data analysis and calculations of the thermal characteristics.

Source link

Rumiana Kotsilkova www.mdpi.com

Greenberg News

Improving Resistive Heating, Electrical and Thermal Properties of Graphene-Based Poly(Vinylidene Fluoride) Nanocomposites by Controlled 3D Printing

2.1. Materials and Nanocomposite Preparation

2.3. Characterization Methods

Greenberg

2.1. Materials and Nanocomposite Preparation

2.3. Characterization Methods

Related Posts

Impact of Hyaluronic Acid and Other Re-Epithelializing Agents in Periodontal Regeneration: A Molecular Perspective

Environmental Factor – September 2023: NIEHS fellows recognized for scientific merit, originality

A new generation of cheaper batteries is sweeping the EV industry

Greenberg