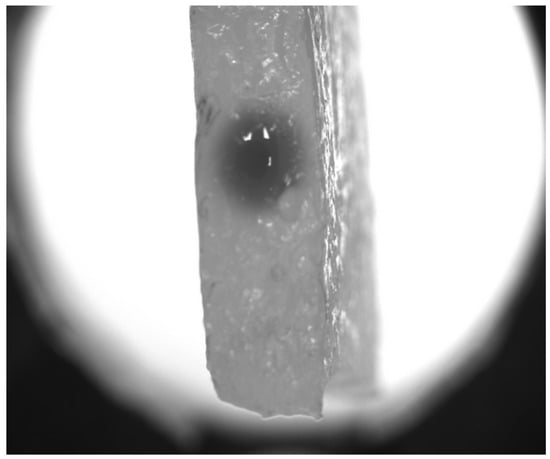
Figure 2 shows the pictures qualitatively illustrating the marker spread with time. One can see an explicit elevation of the visible radius of the spot within hundreds of seconds. A more detailed dynamical picture is provided by the Video S1 assembled from the series of images taken from $0\mathrm{s}$ to $540\mathrm{s}$ separated by the time step of $30\mathrm{s}$. Quantitatively, the central part of the profile is depicted in Figure 3, where solid lines correspond to the cross-sections of the spots presented in Figure 2 and plotted in semi-logarithmic coordinates. Each cross-section passes through the point of symmetry ($x=0$, $y=0$) of the axially symmetric picture. These curves allow us to see the radial spread, but we keep the coordinate x explicitly to account for fluctuations seen in the real experimental records. One can see both widening the profile respectively to the initial condition and diminishing the magnitude of the central plateau, which indicates that the marker dye initially filling the channel leaves it and goes out to the surrounding hydrogel medium.

The latter fact provides an opportunity to estimate whether this spread has a normal diffusion character or not. Even the analytically solved model in the 2D axially symmetric case with constant initial conditions given by a constant concentration spot of a finite radius R results in a complicated integral-based solution. In addition, one can see that real experimental profiles have irregularities. On the contrary, the time evolution of the concentration in the central point possesses a simple analytical solution, which can be rescaled [26] to the form

which results in the linear dependence on time when the diffusion (with the diffusion coefficient D) is normal.

In developing the mathematical model describing the experiment, we implement the model, which generalizes the picture of diffusional spread by taking into account its possible finite velocity of spread tightly connected with the initial relaxation processes. The respective fundamental model is well known as the Cattaneo equation (it also can be referenced as the telegraph equation due to the equivalence of their mathematical structure). The original approach [27] has been considered within the context of addressing the limitations of the classical Fourier law by incorporating a time-dependent term that models finite propagation speeds of thermal signals. It combines features of both hyperbolic and parabolic heat conduction models, making it ideal for studying heat transport in materials where thermal waves are present [28] and exhibiting the transition between two qualitatively different short- and long-time behaviors [29]. It also has applications in studying biological tissues. For example, the Cattaneo equation has been used to model the delayed response of heat conduction that provides a framework for modeling time-lagged responses in heat transfer, especially in tissues subjected to hyperthermia treatments or laser heating [30].

At the same time, the Cattaneo equation-based approach and its generalizations attract attention as a suitable tool for modeling several phenomena related to the random walk [31,32] and anomalous diffusive mass transport [33,34] in complex media. However, the majority of works are limited by purely mathematical considerations without real applications to experimental data.

The classic formulation of the Cattaneo (telegraph) equation, respectively, to the concentration C reads as

where parameter $\tau$ is the relaxation time, indicating the delay before concentration changes respond to the applied gradient. The inclusion of the term ${\partial }^{2}C/\partial t^2$ in Equation (2) implies that changes in C propagate with a finite speed; D is the diffusion coefficient.

The carried out simulations with Equation (2) revealed the crossover effect in the transition from the initial spreading of the dye in the experiment to the diffusive regime with a certain delay similar to the experimental one. However, the regime of the diffusion after the crossover region drastically differs from the experimental one; the reproduction of the dependence of the relaxation shown in Figure 4 was not reproducible for the whole time interval.

Based on this observation and taking into account that the collagen sample is a non-uniform structure and the optic method of registration accesses only the thin upper layer of the finite-depth material, we have to modify Equation (2) for our goal. The respective modification is the equation

where the parameter k accounts for the outflow of the substance either into the bulk of the sample or its “trapping” in the pores of the sample, since the collagen structure is inherently non-uniform.

The simulations with Equation (3) were carried out in the two-dimensional case, i.e.,  the Laplacian was represented as ${\nabla }^2={\partial }^2/\partial x^2+{\partial }^2/\partial y^2$, but under conditions of the axially symmetric spread.

It is worth noting that although the “ideal” initial conditions could be stated as a constant within a disk having the radius R and zero otherwise ($C(x,y,0)=C_0$ if $0<r<R$, $C(x,y,0)=0$ if $r>R$), it is preferable to use the smoother version defined as

where the adjustable parameter s determines the sharpness of the function’s decay from its maximal value $C_0\left(0\right)$ to zero. Such a choice is based on two premises: (i) the Function (4) is differentiable and, as a consequence, the finite-difference scheme implemented for the solution of Equation (3) is more stable; (ii) the actual distribution of the marker in the experiment at the moment corresponding to the initial time of experimental registration also does not have a stepwise shape; see Figure 3. This transient layer is sufficiently narrow and imitates the perivascular space in the biophysical counterpart to the considered model problem. Thus, the value of $s=0.44{\mathrm{mm}}^2$ was chosen by the fitting of Equation (4) to the experimental distribution shown in Figure 3. Simultaneously, the value $R=0.9\mathrm{mm}$ was taken.

Summarizing, the geometry of numerical simulations in comparison to the experimental biomimetic system and the biological meaning of its regions are shown in Figure 5. Note that the radius of the red circle surrounding the central region denoted as “Microvessel” coincides with the radius of a needle used to form a fluid-filled channel in the hydrogel. In fact, the boundary of the channel is something wider due to the mechanical expansion, and this layer of the collagen structure was soaked with the opaque solution of ferroin when it was introduced into the channel with a needle. However, this layer adjacent to the fluid-filled channel can be considered a kind of imitation of the cellular layer forming the BBB (broken in the actual statement of the problem) and the closest part of the perivascular space in biological systems. This interpretation also supports the usage of a continuously changing Function (4), which defines the initial conditions for simulations. Note also that the dark spot in Figure 5A seems wider than the one in Figure 5B by virtue of the grayscale display in the photographic image. In actual simulations, as shown in Figure 3, the numerical values along the diagonal cross-section of the experimental picture and the mathematical model are well coordinated.

The applied modification of the Cattaneo equation implemented in Equation (3) allowed achieving good quantitative correspondence (the coefficient of determination $R^2=0.994$) between results of simulation (the black curve in Figure 4) and the experimental data (circles there). This relaxation curve reproduces the transition between the initial and later stages of the substance spreading. It depicts the first stage with a duration of about 100–150 s as a nonlinear dependence in the used coordinate representation, which originates from the existence of the hyperbolic term in Equation (3) while the second (asymptotic) part is linear that corresponds to the classic diffusive spread. At the same time, it should be noted that the last term in the right-hand side of Equation (3) is crucial for its reproducing, too. Without the leakage, the tangent in the linear region increases more than five times.

We determined the parameters of Equation (3), which provide the mentioned correspondence by the minimization of the absolute deviations between values given its normed solution in the central point at time moments at which the experimental images were taken and the respective values were registered in the real experiment. The values obtained in such a way are listed in the caption to Figure 3. The latter figure allows the exploration of the spatial concentration distribution and its temporal evolution to assess how well the model replicates experimental data under the varying time of the process.

As shown in Figure 3, at the start (the black dashed curve), the concentration profile is the most concentrated near the center, reflecting the initial distribution of the dye. At 120 s, the dye begins to spread, and the peak’s amplitude starts decreasing; however, the reduction is not as rapid, indicating a slight delay. It can be assumed that up to approximately 200 s, a relaxation term plays a significant role. However, with further spreading, diffusion becomes the dominant process, which is somewhat slowed down by a leakage. This is evident at 240 s (see Figure 3, purple dashed and bold lines), where the diffusion process becomes more pronounced, leading to a broader distribution of the dye and a further decrease in the central concentration. Although the experimental curves fluctuate due to the experimental noise and variations in the sample’s structure, the simulated distributions (blue and magenta dashed curves) reasonably reproduce their course on average on the considered radial scales closed to the channel’s surface, i.e., mimicking the processes in paravascular space occurring after the disruption of the blood–brain barrier in the biological case.