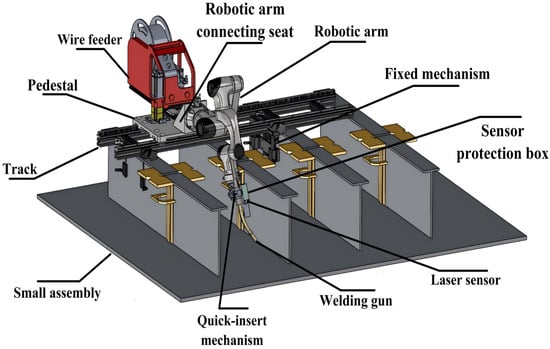
Orbital-Based Automatic Multi-Layer Multi-Pass Welding Equipment for Small Assembly Plates

3.1. Debugging of the Robotic Arm

Before commissioning, it must first be specified that the movement direction of the external axis of the rail is the Z direction in the world coordinate system. The robotic arm, wire feeder, tool flange, quick-plug mechanism, welding torch, and laser sensor are installed onto the bearing mechanism. After the mechanical installation is completed, TCP calibration and laser calibration of the robotic arm are performed. This study adopts the hand-eye calibration method and recommends maintaining a unified calibration posture reference before calibration to prevent precision issues and mechanical arm failures such as lock-up. The starting point of calibration is the flange, which is the end part of the robotic arm. The coordinate system relationships comply with the Cartesian right-hand coordinate system rule shown in Figure 17. During calibration, the coordinate system coincides with the earth coordinate system at the base of the robotic arm, placed at the central position of the robotic arm base, and has the same orientation as the robotic arm’s world coordinate system.

The upper computer processes the hand-eye coordinate system relationship through calibration algorithms and the internal and external parameter matrices of the laser sensor. It converts the relative relationship between the origin of the robotic arm’s Cartesian coordinate system relative to the robotic arm flange into the relative spatial relationship between the origin of the robotic arm base’s Cartesian coordinate system and the sensor’s laser scanning point, as shown in Figure 17. The calibration process requires completing the transformations among the four coordinate systems B, T, C, and CL to obtain the coordinate conversion relationships between two-dimensional pixel coordinates and the spatial coordinate system. The visual recognition results are transferred to the robotic arm’s coordinate system, thereby achieving precise robotic arm motion control and visual guidance. In Figure 17, B represents the robotic arm base coordinate system, T represents the laser sensor coordinate system, C represents the laser sensor coordinate system, and Cl represents the calibration object coordinate system.

For the coordinates of the same point p in any two Cartesian coordinate systems M₁ and M₂ in three-dimensional space, the transformation matrix (1) is a 4 × 4 matrix, which can be represented as the combination H of rotation R and translation T.

$H = [\begin{matrix} R & T \\ 0 & 1 \end{matrix}] = [\begin{matrix} r_{11} & r_{12} & r_{13} & t_{x} \\ r_{21} & r_{22} & r_{23} & t_{y} \\ r_{31} & r_{32} & r_{33} & t_{z} \\ 0 & 0 & 0 & 1 \end{matrix}]$

(1)

In the Equation (1), the submatrix composed of R represents the rotation matrix, and

T (t_{x}, t_{y}, t_{z})

represents the translation vector. The coordinates of point p in

M_{1}

(x_{1}, y_{1}, z_{1})

are transformed into homogeneous coordinates

(x_{2}, y_{2}, z_{2}, 1)

, thereby obtaining the coordinates of point p in

M_{2}

(x_{2}, y_{2}, z_{2})

$[\begin{matrix} x_{2} \\ y_{2} \\ z_{2} \\ 1 \end{matrix}] = [\begin{matrix} r_{11} & r_{12} & r_{13} & t_{x} \\ r_{21} & r_{22} & r_{23} & t_{y} \\ r_{31} & r_{32} & r_{33} & t_{z} \\ 0 & 0 & 0 & 1 \end{matrix}] [\begin{matrix} x_{1} \\ y_{1} \\ z_{1} \\ 1 \end{matrix}]$

(2)

The following coordinate system transformation relationships are expressed as Euclidean transformation matrices: BHCl represents the transformation from the base coordinate system B to the calibration object coordinate system Cl. CHT represents the transformation from the laser sensor coordinate system C to the TCP coordinate system T. This is the “eye-in-hand” relationship; regardless of how many movements occur, the positional relationship between the robotic arm base and the calibration board remains unchanged, and the positional relationship between the laser sensor and the TCP remains unchanged—that is, BHCl and CHT are constants. CHCl represents the transformation from the laser sensor coordinate system C to the calibration object coordinate system Cl, obtained through laser sensor calibration. BHT represents the transformation from the base coordinate system B to the TCP coordinate system T, derived from the robotic arm calibration system. When the robotic arm moves from position 1 to position 2, the following transformation relationships hold:

$B = B H T_{1} \cdot T_{1}$

(3)

$T_{1} = C H T^{- 1} \cdot C_{1}$

(4)

$C_{1} = C H C l_{1} \cdot C l$

(5)

Based on Equations (3)–(5), we obtain (6):

$B = B H T_{1} \cdot C H T^{- 1} \cdot C H C l_{1} \cdot C l$

(6)

Similarly, after the robotic arm moves to position 2, we obtain (7):

$B = B H T_{2} \cdot C H T^{- 1} \cdot C H C l_{2} \cdot C l$

(7)

Combining and rearranging Equations (6) and (7), we derive (8):

$B H T_{2}^{- 1} \cdot B H T_{1} \cdot C H T^{- 1} = C H T^{- 1} \cdot C H C l_{2} \cdot C H C l_{1}^{- 1}$

(8)

If we let

\begin{matrix} X = {C H T}^{- 1}, & A = B H T_{2}^{- 1} \cdot B H T_{1}, & B = {C H C l}_{2} \cdot {C H C l}_{1}^{- 1} \end{matrix}

, we deduce (9):

To solve the problem in the form of Equation (9), we first need to complete the transformation from the base coordinate system to the TCP coordinate system. The rotation matrix is calculated based on the angles of the robotic arm. This paper adopts a specific ZYX Euler angle rotation matrix form to solve BHT. The rotation matrices of the three angles are as shown in Equation (10), where a, b, and c correspond to the (yaw), (pitch), and (roll) angles in the ZYX Euler angles.

$\{\begin{matrix} R_{x} (a) = [\begin{matrix} 1 & 0 & 0 \\ 0 & \cos a & - \sin a \\ 0 & \sin a & \cos a \end{matrix}] \\ R_{y} (b) = [\begin{matrix} \cos b & 0 & \sin b \\ 0 & 1 & 0 \\ - \sin b & 0 & \cos b \end{matrix}] \\ R_{z} (c) = [\begin{matrix} \cos c & - \sin c & 0 \\ \sin c & \cos c & 0 \\ 0 & 0 & 1 \end{matrix}] \end{matrix}$

(10)

Following the sequence of ZYX Euler angles to complete the rotations, multiplying the three matrices yields (11), which expands into (12):

$R = R_{x} (a) R_{y} (b) R_{z} (c)$

(11)

$R = [\begin{matrix} \cos b \cos c & - \cos a \sin c + \sin a \sin b \cos c & \sin a \sin c + \cos a \sin b \cos c \\ \cos b \sin c & \cos a \cos c + \sin a \sin b \sin c & - \sin a \cos b + \cos a \sin b \sin c \\ - \sin b & \sin a \cos b & \cos a \cos b \end{matrix}]$

(12)

A schematic diagram of the ZYX Euler angle rotation is shown in Figure 18.

The homogeneous matrix

{B H T}_{(T)}

is calculated based on

R

$T = {([\begin{matrix} t_{0 x} \\ R & t_{0 y} \\ t_{0 z} \\ 0 & 0 & 0 & 1 \end{matrix}])}^{- 1} [\begin{matrix} t_{t x} \\ t_{t y} \\ t_{t z} \\ 1 \end{matrix}] = [\begin{matrix} T_{x} \\ T_{y} \\ T_{z} \\ 1 \end{matrix}]$

(13)

In Equation (13), (

t_{0 x}, t_{0 y}, t_{0 z}

) are the origin of the base coordinate system, (

t_{t x}, t_{t y}, t_{t z}

) are the origin of the TCP, and (

T_{x}, T_{y}, T_{z}

) record the values of T, denoted as

B H T - T

, which will be used for the calculation of the orthogonal vectors of

C

. In the actual calibration, the eight-point calibration method shown in Figure 19 is adopted for the TCP. These eight points are non-colinear and uniformly distributed within the working space of the robotic arm. The calibration postures need to be manually set, leaving a margin under rotational limit conditions to prevent the robotic arm from locking up or generating singularities. Under the world coordinate system, the robotic arm is operated to sequentially collect and record the position and posture information of the TCP relative to the calibration object. This calibration algorithm uses the J5 axis as the main control axis. In Figure 19a, the TCP of the robotic arm needs to be perpendicular to the calibration object when taking points. In Figure 19b–h, A and B represent the rotational directions around the X and Y axes in the robotic arm’s world coordinate system, and the new posture changes are made as large as possible compared to the previous ones. After point acquisition is completed, calculate the errors. Once they are within the allowable range, operate the robotic arm under the world coordinate system to make its TCP perpendicular to the calibration object and rotate the robotic arm around the A, B, and C axes to check the degree of alignment. Upon passing the verification, the TCP calibration is completed. The smaller the calibration error, the higher the working efficiency and precision of the robotic arm, except when there are errors in the robotic arm itself.

In automatic welding technology, visual sensors are an important component driving the development of intelligent welding [19]. As the “eyes” of robotic arms, visual sensors are also a necessary means of assisting operations [20,21]. Next, we will complete the solution and calibration of the transformation relationship of the laser sensor to achieve precise perception of position and orientation, ensuring the accuracy and stability of scanning recognition. First, we introduce the laser sensor model and use its intrinsic and extrinsic parameter matrices for solving. Both map points from the 3D world to the 2D image plane, i.e., conversion between dimensions. The intrinsic parameters

I P

, related to the internal characteristics of the laser sensor, can be represented as follows (14):

$I P = [\begin{matrix} f & 0 & x_{0} \\ 0 & f & y_{0} \\ 0 & 0 & 1 \end{matrix}]$

(14)

The extrinsic parameters describe the position and orientation of the laser sensor in the world coordinate system, allowing for the transformation from world coordinates to laser sensor coordinates. That is, the extrinsic parameters are

E P = H

. Based on the derivation of the relationship between intrinsic and extrinsic parameters, after performing homogenization operations on the point

p (u_{0}, v_{0})

from the 2D image plane and its spatial coordinates

p (x_{0}, y_{0}, z_{0})

, we obtain the model of the laser sensor, represented as (15).

$λ [\begin{matrix} u_{0} \\ 0 \\ ν_{0} \\ 1 \end{matrix}] = I P \cdot E P \cdot [\begin{matrix} x_{0} \\ y_{0} \\ z_{0} \\ 1 \end{matrix}] o r λ [\begin{matrix} u_{0} \\ 0 \\ ν_{0} \\ 1 \end{matrix}] = [\begin{matrix} f & 0 & x_{0} \\ 0 & f & y_{0} \\ 0 & 0 & 1 \end{matrix}] . [\begin{matrix} r_{11} & r_{12} & r_{13} & t_{x} \\ r_{21} & r_{22} & r_{23} & t_{y} \\ r_{31} & r_{32} & r_{33} & t_{z} \\ 0 & 0 & 0 & 1 \end{matrix}] . [\begin{matrix} x_{0} \\ y_{0} \\ z_{0} \\ 1 \end{matrix}]$

(15)

In (15),

λ

refers to degrees of freedom. During the process of moving from 3D space (laser sensor coordinates) to 2D space (captured image coordinates), one degree of freedom is reduced, particularly depth. The intrinsic parameters focal length (

λ

) and principal point

c_{0} (x_{0}, y_{0})

are provided by the laser sensor. Subsequently, combining the above matrices to solve for the extrinsic parameters, this paper obtains

C H T

by utilizing the projection information of five different calibration points. The calibration transformation relationship is shown in Figure 20.

Using the laser five-point calibration method, a calibration starting center point

u_{c}, v_{c}

and four calibration points at different positions with coordinates

u_{i}, v_{i}

on the target plane are selected, along with the pose parameters of the base coordinate system, with coordinates

(x_{i}, y_{i}, z_{i})

and angles

(a_{i}, b_{i}, c_{i})

, where

i = 1, 2, 3, 4, 5

. Then the offset matrix

M

is prepared.

$M = [\begin{matrix} u_{1} & v_{1} & 1 \\ u_{2} & v_{2} & 1 \\ u_{3} & v_{3} & 1 \\ u_{4} & v_{4} & 1 \\ u_{5} & v_{5} & 1 \end{matrix}]$

(16)

Calculation of

B H T - T

is performed five times according to Equation (13) to obtain

T_{i} (T_{i, x}, T_{i, y}, T_{i, z})

. Based on

M

and

T

, the rotation and translation information is extracted from their product. Then, according to the required orthogonality, the three orthogonal vectors are computed (17).

$\{\begin{matrix} (R_{1} = M^{+} [\begin{matrix} T_{1, x} \\ T_{2, x} \\ T_{3, x} \\ T_{4, x} \\ T_{5, x} \end{matrix}] = [\begin{matrix} r_{11} \\ r_{13} \\ x_{r} \end{matrix}]) (R_{2} = M^{+} [\begin{matrix} T_{1, y} \\ T_{2, y} \\ T_{3, y} \\ T_{4, y} \\ T_{5, y} \end{matrix}] = [\begin{matrix} r_{21} \\ r_{23} \\ y_{r} \end{matrix}]) (R_{3} = M^{+} [\begin{matrix} T_{1, z} \\ T_{2, z} \\ T_{3, z} \\ T_{4, z} \\ T_{5, z} \end{matrix}] = [\begin{matrix} r_{31} \\ r_{33} \\ z_{r} \end{matrix}]) \\ M^{+} = {(M^{T} M^{- 1})}^{- 1} \cdot M^{T} \end{matrix}$

(17)

$V_{1} = [\begin{matrix} r_{11} \\ r_{21} \\ r_{31} \end{matrix}] V_{3} = [\begin{matrix} r_{13} \\ r_{23} \\ r_{33} \end{matrix}] V_{2} = [\begin{matrix} r_{11} \\ r_{21} \\ r_{31} \end{matrix}] \times [\begin{matrix} r_{13} \\ r_{23} \\ r_{33} \end{matrix}] = [\begin{matrix} r_{12} \\ r_{22} \\ r_{23} \end{matrix}]$

(18)

In (17),

M^{+}

represents the pseudoinverse (Moore-Penrose inverse) of

M

. Based on the properties of rotation matrices, we determine that the cross products of the row vectors conform to the right-hand rule, thereby obtaining the relationships among V1, V2, and V3 in (18). Through precise calculations using five calibration points, we derive the optimal approximate solution. In (19),

r_{i j} (i, j = 1, 2, 3)

and

x_{r} y_{r} z_{r}

are variables used to record the results. Subsequently, the variables are normalized.

${\hat{r}}_{i j} = \frac{r_{i j}}{\sqrt{\sum_{i = 1}^{3} r_{i j}^{2}}} (j = 1, 2, 3)$

(19)

The calibration result matrix

X

is constructed, which is the required

C H T^{- 1}

$X = [\begin{matrix} \hat{r_{11}} & \hat{r_{12}} & \hat{r_{13}} & t_{x} \\ \hat{r_{21}} & \hat{r_{22}} & \hat{r_{23}} & t_{y} \\ \hat{r_{31}} & \hat{r_{32}} & \hat{r_{33}} & t_{z} \\ 0 & 0 & 0 & 1 \end{matrix}]$

(20)

For any measurement point

P

with coordinates

p (u_{0}, v_{0})

, it is homogenized to obtain Equation (21).

$p_{B} = {\begin{matrix} B H T & \cdot & C H T \end{matrix}}^{- 1} \cdot p = R \cdot X \cdot [\begin{matrix} u_{0} \\ 0 \\ v_{0} \\ 1 \end{matrix}] = [\begin{matrix} x_{0} \\ y_{0} \\ z_{0} \\ 1 \end{matrix}]$

(21)

The sensor performs repeated emission scanning of laser beams, calculates the time difference and angles of the round trip, and integrates the data to form a more comprehensive two-dimensional data image. Using Equation (21), any two-dimensional coordinate $p (u_{0}, v_{0})$ can be converted into a three-dimensional coordinate $p (x_{0}, y_{0}, z_{0})$ , facilitating further point cloud construction.

In practical operation, the calibration object is placed under the robotic arm’s world coordinate system within the working conditions. A central point and marking points in the four quadrants at different positions within the sensor’s visual range are specified and extracted. As shown in Figure 21a, when adjusting the central point, the laser locator is activated to initiate origin position calibration. The laser beam is superimposed with the positioning beam along the Z and Y axes to obtain the central positioning point. When selecting the four quadrant marking points, refer to the visual range in Figure 21b. The sensor’s field of view divisions and values are as follows: AB is the sensor’s blind zone, BC is the sensor’s positive range, CD is the sensor’s negative range, BD is the sensor’s effective range, C is the sensor’s zero point, W1 is the near measurement end, and W is the far measurement end. All dimensions are in millimeters (mm).

During the process of selecting calibration point data, the four quadrant points should be chosen at optimal distances within the Z/Y axis data intervals specified by the laser’s visual range. Based on the above processing rules, the calibration object is sequentially scanned at the four marking points. The calibration results are then subjected to precision estimation and comprehensive evaluation, and the data are recorded. The calibration result is shown in Figure 22.

Source link

Yang Cai www.mdpi.com

Greenberg News

Orbital-Based Automatic Multi-Layer Multi-Pass Welding Equipment for Small Assembly Plates

3.1. Debugging of the Robotic Arm

Greenberg

3.1. Debugging of the Robotic Arm

Related Posts

Strengthening Climate Action Through Partnerships and Advocacy at COP29

PEPH Newsletter – May 2024

Environmental Factor – June 2023: Exposures affect men’s biological clocks, too

Greenberg