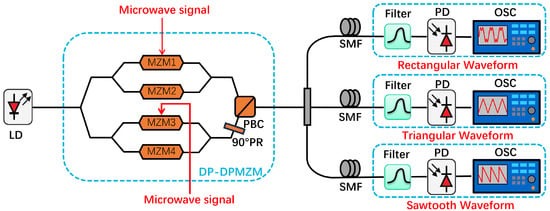
3.1. Experimental Setup
A proof-of-concept experiment was carried out to validate the proposed scheme. An optical carrier at 1550 nm, emitted from an LD, was injected into a commercial DP-DPMZM. Two microwave sources were used for modulation in the experiment to ensure the generation of different waveforms. A sinusoidal signal generated by a microwave signal generator was applied to the MZM1, and a sinusoidal signal was applied to the MZM3. The phase difference between and is zero. After passing through an optical bandpass filter, we acquired two distinct and orthogonal +1st-order sidebands, along with the optical carrier. By applying the optical signal to an optical spectrum analyzer with a resolution of 0.01 nm, the optical spectrum of the modulated optical signal was obtained. The output optical signal was detected utilizing a high-speed photodetector with 3 dB bandwidth of 70 GHz. Subsequently, the electrical signals produced by the photodetector were fed into both an electrical spectrum analyzer and an oscilloscope. The 40 GHz electrical spectrum analyzer was employed to measure the electrical spectra, while the oscilloscope showed the desired microwave waveforms, including triangular, rectangular, and sawtooth waveforms.
3.2. Waveform Generation
Firstly, an
microwave signal at 8 GHz was sent to MZM1, while a 24 GHz
microwave signal was applied to MZM3. MZM1 and MZM3 were all in a carrier-suppressed state by biasing them at minimum transmission points. The powers of RF signals were carefully controlled according to the Principle section.
Figure 3 illustrates the measured optical spectrum at the output of the DP-DPMZM and optical bandpass filter. The corresponding electrical spectrum is depicted in
Figure 4, where the most prominent features are the +1st-order harmonics at 8 GHz and 24 GHz. Since we do not use any electrical amplifiers or optical amplifiers, the final output electrical signal power is not high. In practical applications, power compensation can be used to achieve larger signal output. The power of the 24 GHz harmonic is 19.57 dB lower than that of the 8 GHz harmonic, closely aligning with the theoretical value of 19.08 dB. The 2nd-order harmonic at 16 GHz is effectively suppressed, exhibiting a difference of 41.48 dB compared to the first-order harmonic at 8 GHz. As shown in the waveform of
Figure 4a, a triangular waveform with a repetition frequency of 8 GHz is successfully generated. To assess the approximation error in the waveform, we calculated the RMSE between the measured waveform and the ideal waveform. The RMSE of 0.1089 is close to the theoretical RMSE of 0.0482 calculated from the simulated waveform, and the discrepancy is primarily caused by the external environment and bias voltage instability, among other factors.
Our scheme has the potential for significant tunability and anti-dispersion ability. To further illustrate the tunability of the proposed waveform generation system,
microwave signals with center frequencies of 10 GHz and 12 GHz were loaded to
x-DPMZM, respectively. The corresponding frequencies of the
microwave signals were set at 30 GHz and 36 GHz, respectively, satisfying the required frequency relationship for generating triangular waveforms. The measured electrical spectra and temporal waveforms are shown in
Figure 4c–f. The power of the 30 GHz and 36 GHz harmonics are reduced by 20.23 dB and 20.04 dB, respectively, when compared to the 10 GHz and 12 GHz harmonics. Besides, the RMSE values between the measured and simulated rectangular waveforms are found to be 0.0827 and 0.1384, which fit well with the theoretical values 0.0484 and 0.0484, respectively.
As for the generation of rectangular waveforms, we successfully generated rectangular waveforms with tunable repetition rates. Again, the MZM1 was driven by 8, 10 and 12 GHz
microwave signals, while MZM3 was modulated by 24, 30 and 36 GHz
microwave signals. By biasing MZM1 and MZM3 at the minimum transmission point, the even-order sidebands of x-polarization and y-polarization were effectively suppressed. After filtering to remove undesired sidebands at lower wavelengths and photoelectric conversion, rectangular waveforms with repetition rates identical to the frequency of
microwave signals are generated, as shown in
Figure 5a,c,e. When the
microwave signal was tuned at 8 GHz, it can be seen in
Figure 5b that the power of the desired harmonic at 24 GHz is 9.40 dB lower than that of the 8 GHz harmonic, which is close to the theoretical one of 9.54 dB, and the undesired second-order harmonic at 16 GHz is 30.56 dB lower than first-order harmonic at 8 GHz. The RMSEs of rectangular waveforms were also calculated. For the rectangular waveforms at 8 GHz, 10 GHz, and 12 GHz, the RMSEs between measured waveforms with ideal waveforms were 0.2182, 0.2272 and 0.2507, which were close to the theoretical RMSEs of 0.2020, 0.2019, and 0.2017, calculated between ideal waveforms and simulated waveforms, respectively. To further improve the quality of the rectangular waveform, we can precisely adjust the phase of each harmonic component or utilize a higher sampling rate to capture more high-frequency information.
Subsequently, we demonstrated that the proposed waveform generator is capable of generating other waveforms, such as sawtooth waveforms. By applying an
microwave signal ranging from 8 GHz to 12 GHz to MZM1 and applying an
microwave signal with corresponding frequencies ranging from 16 GHz to 24 GHz to MZM3, the sidebands were precisely controlled to ensure that the frequency relationship complies with Equation (
9). The power ratio between
and
microwave signals was carefully adjusted to satisfy Equation (
9). Both MZM1 and MZM3 were biased at minimum transmission points while ensuring that the DC-introduced phase shifts of
x-DPMZM and
y-DPMZM,
and
were set at
/2. Thus, an optical signal with two orthogonal polarized sidebands and optical carrier was obtained.
In the experiment, sawtooth waveforms with repetition rates identical to the frequency of
microwave signals were generated, as shown in
Figure 6a,c,e. The corresponding electrical spectrums of the sawtooth waveforms are shown in
Figure 6b,d,f. For the sawtooth waveform at 8 GHz, the electrical signals primarily consist of the fundamental tone at 8 GHz and the harmonic at 16 GHz, whose amplitude is 7 dB higher than the fundamental frequency. The contribution from the harmonic at 24 GHz can be neglected, as it is attenuated by 47.23 dB, compared to the fundamental frequency. The RMSEs are 0.1185, 0.1576 and 0.1323 for the sawtooth waveforms with 8, 10 and 12 GHz repetition rates, respectively.
3.3. Anti-Dispersion Transmission
We also verified the anti-dispersion transmission ability of the system. In practical microwave photonic radar applications, different waveforms correspond to different applications. Rectangular signals are commonly used in time-division multiplexing (TDM) systems and digital modulation. Triangular signals are often employed in coherent detection, optical frequency scanning and modulator linearization. And sawtooth signals are widely used in applications such as frequency sweeping, as well as in certain fiber-optic sensing scenarios. This system is suitable for a variety of microwave photonic radar processing systems. In previous work, most photonic generation of microwave waveforms relied on double-sideband modulation, which suffers from power fading during long transmission. The method we proposed is based on carrier-suppressed single-sideband (CS-SSB) modulation. To demonstrate the anti-dispersion transmission and integrity of the waveform after passing the system through 25 km of optical fiber with 5.5 dB loss, we measured the optical spectrum before and after transmission through 25 km single-mode fiber (SMF), as displayed in
Figure 7. It can be seen that there is a power decline when the link includes the 25 km SMF. The optical power attenuated by approximately 5.6 dB.
The temporal waveforms of the generated triangular pulses with repetition rates of 8, 10 and 12 GHz and its electrical spectra correspond to
Figure 8a,b. From electrical spectra, the power fading is approximately 10.84 dB, mainly attributed to insertion loss of SMF.
Figure 8c and d show the time domain waveform and the electrical spectra of the generated rectangular waveforms of 8 GHz, 10 GHz and 12 GHz after passing through 25 km SMF. In addition, we validated the anti-dispersion capability of the system by generating sawtooth waveforms with varying frequencies. The temporal waveforms and electrical spectrum of the generated sawtooth waveforms at 8, 10 and 12 GHz under 25 km SMF transmission condition are depicted in
Figure 8e,f. The power fading observed is approximately 12 dB. We also conducted a comparison between the original 12 GHz triangular waveform and the waveform after transmission through a 25 km optical fiber, both in the time domain and frequency domain. As illustrated in
Figure 9a, the waveform maintains good performance after transmission. The measured spectra in
Figure 9b indicate that the overall electrical power is reduced by approximately 11.2 dB, corresponding to a decrease in optical power of 5.6 dB, which fits well with the insertion loss of the SMF. Therefore, our proposed waveform generator can eliminate power fading due to dispersion over fiber transmission.