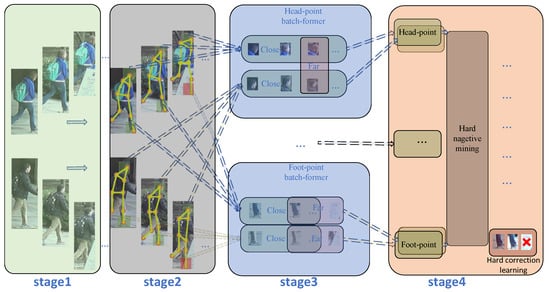
Pose-guided partial-attention is a network architecture that uses pose information extracted by a pose estimator to guide the attention mechanism, aiming to enhance the model’s understanding of local pedestrian features and mitigate the impact of occlusions. Batch information refers to utilizing the relationships among images within the same training batch to enhance feature learning, especially in the context of feature learning for key-point regions of pedestrians. The overall framework of the model is shown in
Figure 2. The model works by first extracting semantic features of key-point regions and global features using a pose estimator and a backbone. It then combines the intensity and direction information between key points to create fused semantic features inputted into KBA. KBA helps to find correlations for the same part in the same batch. Finally, the model performs hard mining on the representation vector after KBA, which is used to correct any wrongly predicted vectors.
The following section describes some details, including those proposed in PPBI, including NON and KBA.
3.2.1. Node Optimization Network
To comprehensively understand the image content and effectively integrate local and global features, this study introduces the NON module. The NON module is inspired by the message-passing mechanism in graph neural networks (GCNs), aiming to dynamically enhance the semantic representation of key-point features while suppressing noise caused by occlusion. Unlike traditional GCNs that assume all node features contribute equally, the NON module introduces a dynamic information propagation mechanism that adaptively adjusts the direction and magnitude of message passing. This enables the NON module to capture both first-order semantic features and high-order edge relationships across different key points. By filtering irrelevant features and emphasizing meaningful semantic relations, the NON module improves robustness under occlusion and varying conditions across different cameras.
A regular graph convolutional layer has two inputs, an adjacent matrix
A of the graph and the features
X of all nodes. The output can be calculated by Equation (
1)
where
is the normalized version of
A and
W refers to parameters of the adjacent matrix.
For the sake of occlusion, we improve the simple graph convolutional layer by adaptively learning the adjacent matrix (a predefined linkage of key-point nodes) based on the global features. Given two local features, we assume the uncovered region’s more meaningful feature is more similar to the global feature. Therefore, we propose a NON module, whose inputs are a global feature
and
K key-point features
, and a predefined matrix (the adjacent matrix is
A). We dynamically update the weights of graph edges by utilizing differences between local features
and global feature
of all key-point nodes, resulting in NON. Then, a simple convolutional graph can be formulated by multiplication between
and NON. To stabilize training, we fuse the input local features
to the output of our NON as in the ResNet. Details are shown in
Figure 3. Our NON can be formulated in Equation (
2), where
and
are two unshared fully connected layers.
Our high-order relation module
is implemented as a cascade of NON to obtain semantic features
from image
x in Equation (
3):
The proposed NON module integrates local and global information by facilitating effective information flow across key-point regions, leveraging multi-scale features to model complex relationships. Additionally, by suppressing meaningless feature transmission from occluded regions, the NON module prevents noise amplification and improves the discriminative power of ReID models.
3.2.2. Learning Key-Point Batch Attention
The above NON outputs a feature vector of size
, where 14 means 13 key points and 1 global feature, and
means batch size. In this part, we utilize the vector of the first 13 key-point vectors, i.e., the vector of size
, as the subsequent input. Then, input each of the 13 key points into the respective KBA model, i.e., the size of each key-point node is
, as shown in
Figure 4.
The 13 key-point nodes represent the different key-point vectors extracted by the model above, representing the 13 most important key regions of the human body. After the model above, these vectors can contain richer information, including the degree of connectivity and directionality between vectors. In the previous methods of dealing with the pedestrian Reid problem by the attention mechanism, the Transformer tends to have a better global field of view, focusing on the global information in a single image. Using this feature of the Transformer, different key points of pedestrians are input into a newly built KBA according to their body key-point parts, in an attempt to obtain the global information between the same key points of different images.
The KBA can effectively learn the relation between the same key-point nodes in an image batch. Such mutual information can effectively close the correlation of the same object while pushing away different objects. For example, there must be a great correlation between the same key-point region of the same pedestrian in other images. In contrast, the correlation between those of the same key region of different pedestrians or the same pedestrian in the case of occlusion will be greatly weakened. This paper learns the 13 key-point nodes separately for the above relationship. When the batch size is appropriate, the same key-point region of the same pedestrian will be greatly correlated. The interference caused by the received occluded part for the matching task will be effectively weakened, which can help predict pedestrian ID in the prediction stage.
The KBA module is motivated by mutual information theory and aims to enhance the model’s ability to capture intra-batch commonalities among key-point features. Unlike traditional approaches that compute mutual information over global features, KBA refines the analysis to the granularity of key points, enabling a more precise and effective representation of shared semantics. By constructing a key-point batch graph, KBA captures the semantic relationships of key points across samples within the same batch. This method not only improves the model’s robustness to occlusion and view variations but also optimizes computational efficiency by limiting the scope of mutual information computation to key-point-level features.
The detailed structure within the KBA is described as follows. As illustrated in
Figure 5, after the preceding network layers, the query vector, key vector, and value matrix
are obtained through three independent linear projections using the representation vector as input. This is followed by the multiplication of the
q and
k vectors to produce an adjacency matrix
A. Upon obtaining the approximate affinity matrix
A, a softmax function
s is typically applied to convert the affinities into attention weights. In this paper, the equation can be rewritten as the sum of two parts, where
p is a small threshold. The first part represents the sum of elements with low attention weights, and the second part represents the sum of elements with high attention weights. Although each attention weight might be small, the total sum remains significant as the number of samples
N increases, making it comparable to the second term in the sum; therefore, irrelevant samples can negatively affect the final computation.
The proposed KBA module highlights the shared semantics among key points within a batch, helping the model focus on consistent and meaningful features while suppressing noise caused by occlusion or background clutter. This fine-grained approach to mutual information significantly enhances the model’s ability to distinguish between occluded features and salient attributes of pedestrians, resulting in improved performance on challenging datasets.
3.2.3. Learning BE
To alleviate the above problems, the BE is proposed in this paper to optimize the degree of correlation between the relevant samples. This paper assumes that if two images are adjacent in the feature space, they will likely be correlated. For this purpose, we propose computing an enhancement mask representing the top k correlation terms from the approximate affinity mapping A, which will focus on the top
k values of affinity in each row. Then, in this paper, we can multiply the Hadamar product with its permutation to obtain an inverse proximity mask. For each element, the value will be set to 1 if both
i and
j are the top k-related terms of each other and 0 otherwise by adding this mask M to the regular softmax function. In this paper, we implement a sparse attention mechanism that exists only in the relevant terms, thus increasing the attention to more pertinent images. The BE is calculated as follows: Since most attention values are set to zero, as shown in
Figure 6, these relations are restricted to similar vectors, making the aggregation in Equation (
4) more focused and robust.
We can obtain
by performing a Hardman product of
and
. The introduction of this augmented mask allows this paper to focus more finely on the critical terms for model training and feature learning. The computation of
is shown in Equation (
5):
In this paper, it is found in practice that the introduction of BE is a sparse attention mechanism, which makes these attention values mainly exist in related terms, thus improving the attention to more associated images. Specifically, since most attention values are zero, these relations focus on the similarity vectors. As a result, the aggregation in the above formulation becomes more focused and robust.
Source link
Jianhai Cui www.mdpi.com