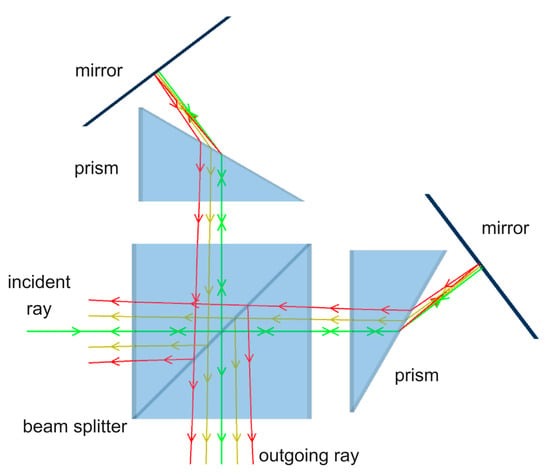
2.1. Movement of the FLP in Prism-Based SHSs
The principle of prism-based SHSs and the phenomenon of the movement of the FLP are briefly described using a typical prism-based SHS [
19]. As shown in
Figure 1, it is based on a Michelson interferometer modified by replacing the mirror in each arm with a prism–mirror assembly. Both mirrors are tilted at the same angle with respect to the prisms in their respective arms. The collimated light enters the beam splitter and is divided into two beams. The beam in each arm passes sequentially through the prism, mirror, prism again, and then returns to the beam splitter. The beam with a certain wavelength, called the Littrow wavelength, will incident perpendicular to the mirror and return parallel to the optical axis. The wave fronts with the Littrow wavelength exiting from the interferometer are perpendicular to the optical axis and produce an interferogram with zero frequency. For a wavelength different from the Littrow wavelength, since the prism has different refractive indices at different wavelengths, the wave fronts of the two outgoing beams are no longer parallel, but tilt at the same angle relative to the optical axis in opposite directions, equivalently producing fringes on the FLP. The FLP can be visualized as a plane of recombination of the two backpropagating beams exiting from the interferometer and should be imaged by the imaging system onto the detector plane.
For traditional grating-based SHSs, the location of the FLP is very intuitive as the beam in each arm is diffracted by the grating only once, so the FLP intersects the center of each grating. However, for the SHSs with a prism–mirror structure, the beam in each arm is refracted more than once by the prism, so there is uncertainty in the location of the recombination plane obtained by extending the outgoing rays from the two arms in the reverse direction. For example, if the apex angle of the prism is set to 30°, the height of the prism is set to 25 mm, the material is set to N-LASF9, the length of the optical axis between the prism and the mirror is set to 16.2 mm, and the Littrow wavelength is 650 nm, the distances from the FLP to the entering surface of the prism if the wavelengths of the incident ray are 400 nm, 600 nm, and 1000 nm are, respectively, about 73.6 mm, 83.5 mm, and 88.6 mm. It can be seen that the location of the FLP is different for different wavelengths of the incident ray, which is consistent with the phenomenon in the experiments done by Fabio Frassetto et al. [
18]: when focusing the imaging optics on a particular FLP distance, a spectral response peaking was obtained at that corresponding wavelength. In fact, the FLP of a point source (ideally) is unlocalized, except that the size of the overlap region of the beams from the two arms varies at different locations. However, even a laser is not an ideal point source and the FLP is localized [
5]. Maintaining a fixed FLP can eliminate the need to calculate the FLP’s location and move the imaging device based on the predicted wavelength of the incident light during use.
2.2. Preliminary Optical Design
To keep the location of the FLP constant, we can make the optical axes of the two arms be turned in opposite directions with respect to each other only once due to refraction. This requires the beam in each arm to pass through the prism only once. After the beam passes through the prism, it needs to return to the beam splitter without passing through the prism again. Therefore, some form of optics is needed to reflect the beam and provide a shift.
To realize this idea, we propose to use a prism–bimirror–mirror assembly instead of the prism–mirror structure in each arm, as shown in
Figure 2a, with the angle made by the two planes of the bimirror being a right angle. The collimated light is split by a beam splitter and is divided into two paths. Now we will describe only one of the paths. The beam is incident vertically into a prism and refracted at its exiting surface. Then, the beam is incident to one of the planes of the bimirror. The intersection line of the two planes of the bimirror is perpendicular to the incoming axis of the bimirror and parallel to the side surfaces of the prism. In terms of the direction of the beam, a right-angle bimirror is equivalent to a mirror, except that the beam is shifted by an extra segment of the optical axis between the incoming and outgoing axes, which staggers the incoming and outgoing beams.
To allow the beam to return to the beam splitter for recombination with another one, a mirror is added behind the bimirror to change the direction of the optical axis. This mirror is tilted at a proper angle so that its outgoing optical axis is perpendicular to the surface of the cube beam splitter. The system is a TSHS in which the Littrow wavelength can be tuned by tilting the bimirrors and the mirrors. The rotating spindle is located at the refracting surface of the prism, intersecting the center of the refracting surface, as well as at the mirror, intersecting the center of the mirror. The bimirror and mirror share this spindle, where the bimirror needs to be tilted twice as much as the mirror during the tuning process. The prism–bimirror–mirror structures of the two arms are upside down with respect to each other in order to ensure that the outgoing beams from the two arms are tilted in opposite directions, as shown in
Figure 2b.
If the wavelength of the incident light is not equal to the tuned Littrow wavelength, the wave fronts of the beams of the two arms are tilted by the same angle relative to the optical axis in opposite directions, equivalently producing the fringes on the FLP. The center of the FLP overlaps with the center of the refracting surface of each prism. The distance from the FLP to the imaging optics is equal to the length of the optical axis between the refracting surface of each prism and the imaging optics. This length does not change, regardless of the tuned Littrow wavelength and the wavelength of the incident light, solving the problem of the FLP location varying with the wavelength that exists in current prism-based SHS designs.
Besides diffused light, stray light can be generated by specular reflection on the surfaces of the cube beam splitter and prisms. Anti-reflection (AR) coatings are needed to improve transmittance. In the arrangement shown in
Figure 2, the splitting and recombination of the beams occur at different locations in the beam splitter, preventing the beams from reaching the detector without passing through any arm. In addition, the prisms are single- rather than double-passed, which may result in less chance for the beams to be reflected by the prisms. Stray light analysis requires the consideration of many other factors such as mechanical structure and still requires further research.
An added advantage of this system is that the outgoing beams in the two different directions are not backtracking toward the source. The two outgoing beams can be detected by two detectors to increase the luminous flux. This advantage remains if the prisms are replaced by gratings, which is not discussed further in this paper.
2.3. Spectral Inversion
The parameters of the key components in the Zemax OpticStudio v.19.4 simulation are provided here first. The glass of each prism used is N-LASF9 (SCHOTT Group Corporation, Mainz, Germany) and the apex angle of each prism is 30°. The half-width of the incident light is 20 mm. The imaging system has a magnification of 0.5. The parameters of the detector refer to the SONY IMX 174 (Sony Group Corporation, Tokyo, Japan), which has a pixel pitch of 5.86 µm and 1936 × 1216 pixels.
Assuming that the wavelength of the incident light is not equal to the tuned Littrow wavelength, the equivalent fully transmissive optical system is shown in
Figure 3a and the wave fronts intersecting the centers of the refracting surfaces of the prisms of the two arms are shown in
Figure 3b. Assuming points A and B on the two wave fronts are from any point on the light source, the two beams propagate in the directions AC and CB, respectively. They are equivalent to intersecting at point C. Thus, the FLP intersects the center of the refracting surface of each prism and is perpendicular to the outgoing optical axis of each prism. The center of interference is always located at the center of the FLP and the values of the optical path difference (OPD) at both ends of the FLP are the largest.
If the angle between each wave front and the FLP is
β, then the
OPD is
Then, the spatial frequency
f of the interferogram is
where
σ is the wavenumber of the incident light, which is the reciprocal of the wavelength
λ. Setting the Littrow wavelength as
λ0, the angle
β between the wave front and the FLP is
The refractive index
n versus wavelength
λ equation for the N-LASF9 provided in the Glass Catalog of ZEMAX is
The coefficients of the formula are K1 = 2.00029547, L1 = 0.0121426017 µm2, K2 = 0.298926886, L2 = 0.0538736236 µm2, K3 = 1.80691843, and L3 = 156.530829 µm2. The correspondence between the spatial frequency f of the interferogram on the FLP and the wavelength λ of the incident light has been established up to this point. Compared to the SHS with a prism–mirror structure, it has a much simpler inversion formula.
2.4. Performance Parameters
Now, we calculate the theoretical spectral resolving power of the system. Assuming that the incident light with a wavenumber of
σ1 produces 2
N fringes, the maximum
OPD on the interferogram can be expressed as
Nλ1. If the half-width of the light source is
d0, due to the small angle between the wave fronts of the two arms and the FLP, the half-width
d of the wave fronts of the two arms after passing through the refracting surfaces of the prisms can be approximated as
Thus, the maximum
OPD can also be expressed as
where β1 is the angle between each wave front and the FLP when the wavelength of the incident light is λ1. Since β1 is small, substituting Equation (3) into Equation (6), we can approximately get
Assuming that the number of fringes increases by one when the wavenumber of the incident light changes to
σ2, the same way we obtain
The difference between these two wavenumbers is the maximum spectral resolution. When defining the function,
Combining Equation (7) and Equation (8), we can get
Since the difference between
σ1,
σ2 and
σ0 is small at a given tuning, the following approximation can be made:
where f′(σ) denotes the derivative function of f(σ). Substituting Equation (11) into Equation (10), we can get the maximum spectral resolution:
The theoretical spectral resolving power of the system at wavenumber
σ can be expressed by the following equation:
The variation of the theoretical spectral resolving power of the spectrometer is shown in
Figure 4. The theoretical spectral resolving power in the spectral range (10,000 cm
−1~25,641 cm
−1) is approximately 1381~27,595; that is, the highest spectral resolution is approximately 0.014 nm/390 nm (0.93 cm
−1/25,641 cm
−1). In some applications, the required spectral resolving power differs in different spectral ranges, allowing the selection of the appropriate material and apex angle for the prisms accordingly.
Next, consider the tuning angles of the system. According to the Nyquist–Shannon theorem, spectral information can be recovered if a detector uniformly samples an interferogram at a frequency that exceeds the fringe frequency by at least a factor of two. The spectral range of an arbitrary tuning is limited by the maximum fringe frequency of the interferogram, which is determined by the pixel pitch of the detector. In the simulation in this paper, six tuning steps are required to achieve detection in the range of 0.39 µm to 1 µm: the angles of the mirror tilt with respect to its outgoing optical axis are 20.99°, 20.51°, 20.01°, 19.44°, 18.78°, and 18.19°, respectively corresponding to Littrow wavelengths of 0.398 µm, 0.420 µm, 0.450 µm, 0.500 µm, 0.600 µm, and 0.800 µm. The bimirror is tilted at twice the angle of the mirror to ensure that its outgoing optical axis is aligned with the incoming optical axis of the mirror.
Finally, consider the usable FOV. In SHS, the limiting off-axis angles are reached when the OPD at the edge of the fringe pattern changes by 1/2 wavelength. Since the usable FOV is negatively correlated with the spectral resolving power, the usable FOV when the incident light is at the wavelength with maximum spectral resolving power (0.39 µm) determines the usable FOV of the instrument. By setting the conditions to get a series of solutions and fitting the relationship between
ϕ and
φ,
where ϕ denotes the angle between the on-axis rays and the component of the off-axis rays in the dispersion plane and φ denotes the angle between the off-axis rays and the dispersion plane. The FOV of this system is comparable to that of the typical prism-based SHS shown in Figure 1 in cases of equal spectral resolving power.
2.5. Simplification of the Motion Control System
Tuning the spectrometer with the structure shown in
Figure 2 requires tilting four optics: two bimirrors and two mirrors. The motion control system is more complex than that of a grating-based TSHS, which requires tilting only two gratings. We drew on the orthogonal interferometer based on a Michelson interferometer designed by Li Yixuan et al. [
20] and modified it into the form of a Mach–Zehnder interferometer. After simplifying the motion control system, it allows tuning by tilting only two optics at the expense of a larger spectrometer size. As shown in
Figure 5a, the collimated light is divided by the beam splitter into arm A and arm B. Arm A contains mirror 1 and arm B contains a bimirror. The angle between the two mirrors of the bimirror is 90°. The mirror 1 and bimirror, each placed at 22.5°, reflect the beams onto a right-angle prism coated with mirrors. Then the two beams incident parallelly to prism 1 and prism 2, respectively. The bimirror acts like a roof prism, deflecting the beam top-to-bottom.
When the beams of the two arms are incident into the prisms placed in the same direction, the cross-section of the beam of arm B is upside down. Thus, while the two beams are refracted by the prisms in a same outgoing direction, they are equivalent to being tilted at the same angle relative to the optical axis in opposite directions. After this, the beams of the two arms pass through the bimirror assembly and mirror 2 and return to the right-angle prism in turn. Then, the beam of arm A passes through mirror 1 again and the beam of arm B passes through the bimirror again, being deflected bottom-to-top. Finally, the two beams return to the beam splitter for recombination.
This modified structure assembles the two bimirrors of the two arms of the prism–bimirror–mirror TSHS into a bimirror assembly by fixing them together and tilting them synchronously. Similarly, the two mirrors of the two arms are combined into mirror 2. Therefore, tuning can be performed by simply tilting the bimirror assembly and mirror 2 around the rotating spindle, simplifying the motion control system.
2.6. Anti-Aliasing Design
One of the major limitations of SHS is that the symmetry in achieved spectrum from the Fourier transform duplicates all spectrum features at locations on either side of the Littrow wavelength λ0, which is referred to as aliasing. If λ1 > λ0, the spatial frequency f of the interferogram corresponds to λ1 one-to-one; if λ2 < λ0, f also corresponds to λ2 one-to-one. Therefore, a spatial frequency f corresponds to two wavelengths, λ1 and λ2. We need an additional mechanism to tell the difference between λ1 and λ2.
For grating-based SHSs, each grating can be tilted by a small, constant angle around the axis of symmetry which is perpendicular to the tuning spindle. This tilting produces a constant frequency in a direction orthogonal to the interference fringes generated by dispersion. However, in prism-based SHSs, if the mirrors are tilted, the FLP of the fringes produced by dispersion is at a different location than the FLP of the fringes orthogonal to the direction of dispersion. If the prisms are tilted, this will lead to a change in the refractive angle, which may have an effect on the accuracy of the spectrum [
20]. This is acceptable if the resolution of the spectrometer is not very high.
We consider tilting only half of the areas of the refracting surfaces of the prisms of both arms by a small angle (0.1°) around their axes of symmetry which are perpendicular to the tuning spindle, as shown in
Figure 5b. This results in both a 1D interferogram and a 2D interferogram on the FLP, where the 1D interferogram recovers the exact spectrum and the 2D interferogram is used to differentiate between
λ1 and
λ2. Now, we describe the principle of the 2D interferogram. The beams pass through half of the refracting surfaces that are tilted and not only produce the angle
β with the optical axis in the dispersion plane, but also produce an angle
γ with the optical axis in the direction orthogonal to the dispersion plane. When the beams are recombined by the beam splitter, the angles become +
γ and –
γ, because the beam from one arm is transmitted and the beam from the other arm is reflected. The plus or minus sign of
γ is determined by which arm the beam is coming from and is independent of the wavelength, which makes the states of the outgoing beams corresponding to
λ1 and
λ2 different. The interferograms are modulated in the direction orthogonal to the dispersion plane. In the simulations in this paper, when
λ1 >
λ0, the interferogram is deflected clockwise and the impact spectrum of the 2D power spectrum is located in the first and third quadrants; when
λ2 <
λ0, the interferogram is deflected counterclockwise and the impact spectrum is located in the second and fourth quadrants.
Source link
Zihao Liu www.mdpi.com