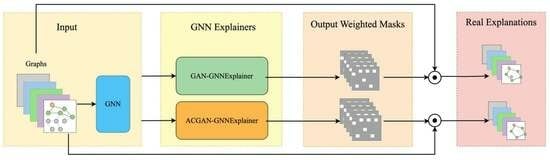
Reliable and Faithful Generative Explainers for Graph Neural Networks

4.1. Experimental Settings

Datasets. We focus on two commonly used synthetic node classification datasets, BA-Shapes and Tree-Cycles [9], as well as two real-world graph classification datasets, Mutagenicity [33] and NCI1 [34]. Detailed descriptions of datasets are provided in Table 1.

The BA-Shapes dataset comprises a Barabasi–Albert (BA) graph with 300 nodes. It incorporates 80 “house”-structured network motifs randomly attached to nodes within the base graph. Nodes are classified into four categories based on their structural roles: those at the top, middle, and bottom of houses and those not part of any house.

The Tree-Cycles dataset originates from an initial eight-level balanced binary tree. It incorporates 80 six-node cycle motifs attached randomly to nodes within the base graph. Nodes are divided into two classes based on whether they belong to the tree or the cycle.

The Mutagenicity datasets consist of 4337 molecule graphs representing atoms as nodes and chemical bonds as edges. These graphs are categorised into two classes, nonmutagenic and mutagenic, indicating their effects on the Gram-negative bacterium Salmonella Typhimurium. Specifically, carbon rings containing $N H_{2}$ or $N O_{2}$ groups are known to be mutagenic. However, carbon rings are present in both mutagenic and nonmutagenic graphs, rendering them nondiscriminative.

NCI1 is a curated subset of chemical compounds evaluated for their efficacy against non-small-cell lung cancer. It encompasses over 4000 compounds, each tagged with a class label indicating positive or negative activity. Each compound is depicted as an undirected graph, with nodes representing atoms, edges denoting chemical bonds, and node labels indicating atom types.

Baseline approaches. With the rising adoption of GNNs in various real-world applications, the need for explainability has gained significant attention, as it plays a crucial role in enhancing model transparency and building user trust. In this context, we selected three prominent GNN explanation methods for comparison: GNNExplainer [9], Gem [12], and OrphicX [26]. For these methods, we utilised their official implementations to ensure consistency in evaluation.

Different top edges (K or R). After calculating the importance (or weight) of each edge in the input graph G, selecting an appropriate number of edges for the explanation is crucial. Choosing too few edges may result in incomplete explanations, while selecting too many can introduce noise. To address this, we define a top K for synthetic datasets and a top ratio (R) for real-world datasets to determine the number of edges to include in the explanation. We evaluate the stability of our method by experimenting with different values of K and R. Specifically, we use $K = 5, 6, 7, 8, 9$ for the BA-Shapes dataset, $K = 6, 7, 8, 9, 10$ for the Tree-Cycles dataset, and $R = 0.5, 0.6, 0.7, 0.8, 0.9$ for the real-world datasets.

Data split. To ensure consistency and fairness in our experiments, we split the data into three subsets: 80% for training, 10% for validation, and 10% for testing. The testing data are kept completely separate and unused until the final evaluation stage.

Evaluation metrics. An effective GNN explainer should produce concise explanations or subgraphs while preserving the model’s predictive accuracy when these explanations are input back into the target GNN. Therefore, it is essential to assess the performance of the explainer using multiple evaluation metrics [35]. In our experiments, we evaluate the accuracy of the GAN-GNNExplainer and assess both the accuracy and fidelity of the ACGAN-GNNExplainer.

Specifically, we generate explanations for the test set using GNNExplainer [9], Gem [12], OrphicX [26], GAN-GNNExplainer, and ACGAN-GNNExplainer. These explanations are then fed into the pre-trained target GNN model f to evaluate the accuracy, which is formally defined in Equation (9):

$A C C_{e x p} = \frac{| f (G) = f (G^{s}) |}{| T |},$

(9)

where G represents the original graph requiring explanation and $G^{s}$ refers to its corresponding explanation (such as the significant subgraph). The term $| f (G) = f (G^{s}) |$ denotes the number of instances where the predictions of the target GNN model f on both G and $G^{s}$ are identical, while $| T |$ is the total number of instances.

Furthermore, fidelity assesses how accurately the generated explanations capture the key subgraphs of the original input graph. In our experiments, we utilise the metrics

F i d e l i t y^{+}

and

F i d e l i t y^{-}

[36] to evaluate the fidelity of the explanations.

F i d e l i t y^{+}

measures the change in prediction accuracy when the key input features are excluded, comparing the original predictions with those generated using the modified graph. Conversely,

F i d e l i t y^{-}

evaluates the variation in prediction accuracy when the important features are retained and nonessential structures are removed. Together,

F i d e l i t y^{+}

and

F i d e l i t y^{-}

offer a comprehensive assessment of how well the explanations capture the model’s behaviour and the significance of various input features. The mathematical definitions of

F i d e l i t y^{+}

and

F i d e l i t y^{-}

are provided in Equation (10) and Equation (11), respectively:

$F i d^{+} = \frac{1}{N} \sum_{i = 1}^{N} (f {(G_{i})}_{L_{i}} - f {(G_{i}^{1 - s})}_{L_{i}}),$

(10)

$F i d^{-} = \frac{1}{N} \sum_{i = 1}^{N} (f {(G_{i})}_{L_{i}} - f {(G_{i}^{s})}_{L_{i}}),$

(11)

where N represents the total number of samples and $L_{i}$ denotes the class label for instance i. The terms $f (G i) L_{i}$ and $f (G i^{1 - s}) L_{i}$ refer to the prediction probabilities for class $L_{i}$ based on the original graph $G_{i}$ and the occluded graph $G_{i}^{1 - s}$ , respectively. The occluded graph is created by removing the important features (explanations) identified by the explainers from the original graph. A higher $F i d e l i t y^{+}$ value is preferred, indicating a more critical explanation. On the other hand, $f (G i^{s}) L_{i}$ refers to the prediction probability for class $L_{i}$ using the explanation graph $G_{i}^{s}$ , which contains the crucial structures identified by the explainers. A lower $F i d e l i t y^{-}$ value is desirable as it reflects a more complete and sufficient explanation.

In summary, the accuracy of the explanation ( $A C C_{e x p}$ ) evaluates how well the generated explanations reflect the model’s predictions, while $F i d e l i t y^{+}$ and $F i d e l i t y^{-}$ measure the necessity and sufficiency of these explanations, respectively. By comparing the accuracy and fidelity metrics across different explainers, we can gain meaningful insights into the effectiveness and suitability of each method.

Source link

Yiqiao Li www.mdpi.com

Greenberg News

Reliable and Faithful Generative Explainers for Graph Neural Networks

4.1. Experimental Settings

Greenberg

4.1. Experimental Settings

Related Posts

Greenpeace statement on Gaza ceasefire deal

Causes, Impacts and Recovery – State of the Planet

The Most Eco- (and Budget) Friendly Heating Options this Winter

Greenberg