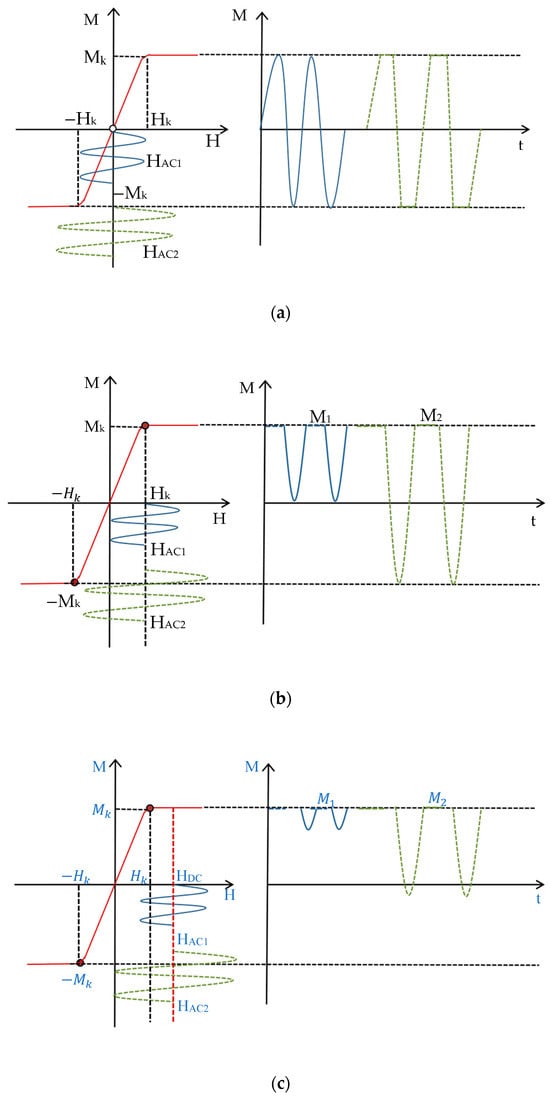
2.1. Second Harmonic Response Analysis of Magnetic Nanoparticles
Neglecting magnetic particle anisotropy, particle–particle interactions, and hysteresis, the nonlinear magnetization behavior of superparamagnetic iron oxide nanoparticles can be approximated by the Langevin paramagnetic theory. When exposed to an external magnetic field, the magnetic moments of these particles align with the field direction, resulting in a change in magnetization. For ideal particles, magnetization increases gradually with increasing field strength, reaching saturation, and subsequently decreases to zero as the field is removed. This behavior can be mathematically modeled using the Langevin function [
28].
The average magnetic moment in the direction of the applied magnetic field, denoted by ⟨m⟩, is determined by the magnetic moment of the nanoparticles (m), the applied magnetic field strength (H), the absolute temperature (T), and the Boltzmann constant (kB).
Figure 1 shows the schematic diagram of magnetic nanoparticles based on different harmonics detection:
M–
H is the nonlinear magnetization response curve of the magnetic nanoparticles,
M is the magnetization signal,
Mk is the saturation magnetization signal,
H is the applied magnetic field strength,
Hk is the applied magnetic field strength required for the magnetic nanoparticles to reach the saturation magnetization signal,
M–
t is the time-domain graph of the magnetic nanoparticles’ magnetization signals, and M1 and M2 are the magnetization response of the magnetic nanoparticles at the same frequency with different amplitudes. In particular,
Figure 1a represents the principle of MNP detection using the third harmonic response. If a small amplitude AC magnetic field (
) is applied, the magnetization response is sinusoidal and contains the fundamental frequency; the magnetization response obtained by applying a large-amplitude AC magnetic field (
) is distorted and contains the third and odd harmonics. By attaching a DC bias field
to the AC magnetic field, as shown in
Figure 1b, the AC field is shifted, and the magnetization response of the magnetic nanoparticles is a half-rectified waveform, which generates even harmonic signals, mainly the second harmonic. When
, the second harmonic signal of the magnetic nanoparticles reaches the maximum value due to the nonlinear characteristics of its magnetization signal; when
, the rectified waveform of the magnetic particles’ magnetization response time-domain graph becomes smaller, as shown in
Figure 1c, and the time-domain curve tends to be saturated gradually with the second harmonic acceptance signal being zero as
increases. As can be seen from
Figure 1, based on the second harmonic, the magnetic particle magnetization signal is not affected by the AC field amplitude. Even if the AC field amplitude is small, the particle magnetization response can be observed.
The red curve on the left side of the figure shows the nonlinear magnetization response curve of the magnetic nanoparticles; the small amplitude (HAC1) sinusoidal AC voltage waveform is shown in blue, and the green dotted line is the large amplitude (HAC2) sinusoidal AC voltage waveform. The curves on the right side of the figure are the time-domain graphs of the magnetic nanoparticle magnetization signals at the same frequency with different amplitudes.
The application of a DC bias to the alternating magnetic field results in a total applied magnetic field
H that is the sum of the excitation field and the DC bias field.
Substitute into Equations (1) and (2):
The magnetization of the
k-th harmonic signal is as follows [
30] (where the exponent
i is the first
i particle signals summed over the magnetized intensity of the kth harmonic signal):
The magnetized signal
M is expanded by the Taylor series and decomposed into the harmonic signal amplitude intensity
A (signal peak) of each order, where the second harmonic amplitude intensity
(signal peak) can be expressed as follows:
where N represents the concentration, Ms is the saturation magnetization of the magnetic nanoparticles (MNPs), HAC is the AC field strength, HDC is the DC field strength, kB is the Boltzmann constant, and T is the absolute temperature. Given the known values for the MNP concentration, Boltzmann constant, temperature, and saturation magnetization of the sample material, the dependence of the second harmonic signal on the DC and AC excitation fields is illustrated in Figure 2. As shown, the second harmonic signal of the MNPs increases rapidly with the DC bias field until it reaches a peak and subsequently declines. This behavior stems from the nonlinear magnetization characteristics of MNPs. Furthermore, increasing the AC excitation field drives the magnetization signal from the linear regime to the saturation regime.
As depicted in
Figure 1, the introduction of a DC bias field shifts the AC excitation field. When 0 <
HDC <
Hk, the magnetization curve exhibits asymmetric distortion in the time domain, resulting in an increased induced electromotive force (EMF). At
HDC =
Hk, the magnetization response becomes a half-rectified waveform, yielding a maximum second harmonic signal. When
HDC >
Hk, the time-domain magnetization signal exhibits small-amplitude fluctuations, ultimately approaching saturation (
M =
Ms) and resulting in a null induced EMF.
2.2. Establishing the Relationship between Bias Field and Sample Spatial Distance Based on Langevin Equation
In practical applications, the excitation magnetic field is typically generated by a solenoid, which can be approximated as a superposition of the magnetic fields produced by a finite number of toroidal coils. While a toroidal coil generates its maximum magnetic field at its center, the sample is often positioned at a distance from the excitation coil, resulting in a weaker magnetization. The magnetic field distribution is illustrated in
Figure 3.
It is assumed that the toroidal coil is on the
xyz-axis coordinate system, the center of the coil coincides with the coordinate origin O, and the radius of the coil is R; ds is the element per unit of length, r is the distance from the length element to the detection point P, and
is the vector of r. The magnetic field at the detection point P must be along the
x-axis, i.e., (x, 0, 0). Due to the axial symmetry, the dB_y components of the magnetic field cancel each other, and the synthetic field at point P must be along the
x-axis, i.e., (x, 0, 0).
Figure 4 shows the analysis of the magnetic field and the coordinate system of the detection point P on the axis.
According to the Biot–Savart Law:
Substituting ∮ds = 2πR into the preceding equation yields the following expression for B
x:
Equations (1)–(8) demonstrate that as point P moves along the axial direction (increasing x), the induced magnetic field decreases. The total magnetization of the magnetic nanoparticles is given by
where = βmB, N refers to the total number of magnetic particles, β = 1/kBT.
Figure 5 depicts the Langevin function as a function of
= βmB. As the detection distance d increases, the induced magnetic field B decreases, resulting in a decrease in the slope of the function
/3. Consequently, a larger DC bias field is required to saturate the second harmonic magnetization signal of the magnetic nanoparticles.
2.3. Probe Structure Design
To minimize sensor volume and shield the detection signal from interference generated by the excitation coil, surrounding circuits, and external DC magnetic fields, an anti-interference differential coil structure is employed, as shown in
Figure 6. The outermost layer contains the excitation coil, responsible for generating the magnetic field used to stimulate the nanoparticles. The inner layer consists of two detection coils, wound with an equal number of turns but in opposite directions, connected in series for differential mode operation. This configuration maximizes the extraction of the signal from the sample. The nested coil structure effectively cancels the in-phase induced potential from the excitation field within the detection coils, significantly reducing noise and enhancing the signal-to-noise ratio (SNR).
The particle generates an induced magnetization signal under the action of an applied excitation magnetic field, and the receiving coil receives the particle magnetization signal. Wherein coil 1 senses the excitation magnetic field signal
u1, coil 2 senses the particle signal uc superimposed with the excitation magnetic field signal
u2, and the coil 2 and coil 1 differential signal is
Since the coil 1 and coil 2 currents are in opposite directions and in series with each other, then
The detection signal is obtained as
The detection coil is constructed using 790 turns of 1 mm diameter Litz wire, with a 30 mm separation between the two coil sections. Operating at a frequency of 8642 Hz, the coil exhibits an inductance of 3.74 mH and a resistance of 31.57 ohms. To amplify the second harmonic signal at 17,284 Hz, a resonant capacitor is connected in parallel with the detection coil, forming an LC parallel resonant circuit. This circuit enhances the voltage of the signal at the resonant frequency. The value of the resonant capacitance is calculated using the following formula:
where ω represents the angular frequency of resonance and L represents the inductance of the detection coil. The quality factor (Q) of the resonant circuit is given by
and detection sensitivity is given by
where Vs represents the voltage signal generated across one side of the coil, S denotes the cross-sectional area of the coil, and N corresponds to the number of turns in the coil.
The probe utilizes a differential detection principle based on a nested coil structure. An alternating magnetic field generated by the excitation coil induces a nonlinear response in the magnetic nanoparticles, which is subsequently detected by the detection coil. The detection coils, positioned symmetrically above and below the sample, are connected in series with reversed polarity, effectively canceling out induced potentials from the excitation field. Conversely, the nonlinear echo signals emanating from the target nanoparticles are detected primarily by a single coil. This spatial arrangement minimizes interference from the excitation field, thereby amplifying the signal from the target nanoparticles.