2.1. Measurement Principle of the Inductive Conductivity Sensor
The measurement principle of inductive conductivity sensors is based on Faraday’s law of electromagnetic induction, enabling the non-contact detection of liquid conductivity. The sensor probe typically consists of two primary components: an excitation coil and a sensing coil, together forming an electrode-free measurement structure. This configuration effectively eliminates the interference from electrode contamination and polarization effects, ensuring long-term stability and reliable performance. When alternating current is applied to the excitation coil, it generates a time-varying magnetic field. This magnetic field induces eddy currents in the conductive medium, which in turn generate a secondary magnetic field that is detected by the sensing coil. The magnitude of the induced current is directly proportional to the conductivity of the liquid, allowing the conductivity to be measured without direct contact with the fluid.
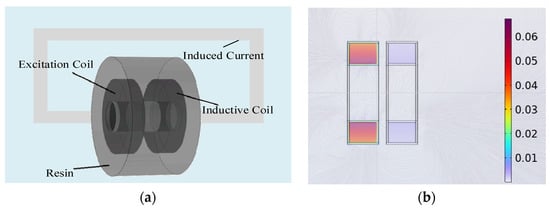
The structure of the inductive conductivity sensor probe is shown in
Figure 1a. According to Faraday’s law of electromagnetic induction, the application of alternating current to the excitation coil produces an alternating magnetic field that extends through the sensor and into the surrounding liquid. This magnetic field induces eddy currents (or induced currents) in the conductive medium, the strength of which is directly related to the liquid’s conductivity. The induced currents generate a secondary alternating magnetic field within the liquid, which induces an electromotive force (EMF) in the sensing coil. Since the conductivity of the liquid determines the strength of the induced current, it directly influences the output signal of the sensing coil. By measuring the amplitude and frequency characteristics of the signal from the sensing coil, the conductivity of the liquid can be inferred.
Figure 1b shows the magnetic flux density distribution of the sensor probe, which is obtained through finite element simulation. The excitation coil magnetically couples with the sensing coil through the conductive liquid, inducing magnetic flux in the magnetic core of the sensing coil. This, in turn, generates an electromotive force (EMF) in the sensing coil, which is then used to measure the conductivity.
A virtual short-circuit circuit, constructed using an operational amplifier, is employed to measure the sensor output, as shown in
Figure 2. The excitation signal, generated by the signal generator and power amplification module, is applied to the excitation coil. The measured liquid is modeled as a single-turn coil, with its conductivity represented by a resistance
Rs, which is placed between the excitation coil and the sensing coil, creating a coupling mechanism that generates an output signal at the sensing coil. Due to the virtual short-circuit property of the operational amplifier, the output of the sensing coil is effectively short-circuited. The short-circuit current
I4 is influenced by the conductivity of the measured liquid, the geometry of the sensor, and the excitation frequency. Once the sensor’s structure and operating conditions are fixed, the short-circuit current
I4 becomes directly proportional to the conductivity of the measured liquid. Exploiting the virtual open-circuit property of the operational amplifier, the short-circuit current
I4 flows through the feedback resistor
Rf, following the relationship
Uout =
Rf ×
I4. Therefore, by measuring the output voltage
Uout of the operational amplifier, the conductivity of the measured liquid can be determined.
2.2. Equivalent-Circuit Model of the Inductive Conductivity Sensor
The equivalent circuit of the inductive conductivity sensor is shown in
Figure 3 [
18]. The sensor consists of an excitation coil and a sensing coil with electromagnetic coupling established through the measured liquid. In the equivalent circuit, the coupling between the excitation coil, the liquid, and the sensing coil is modeled as the coupling of two ideal transformers. The excitation coil and the sensing coil are magnetically coupled through the conductivity of the liquid. In
Figure 3,
L1 and
L4 represent the inductance of the excitation coil and the sensing coil, respectively, while
L2 and
L3 represent the equivalent inductance of the liquid. The mutual inductance between the coils and the liquid is represented by
M12 and
M34. However, due to shielding measures typically implemented between the excitation coil and the sensing coil, the mutual inductance between the two coils is generally neglected in this model. The resistances
R1 and
R2 correspond to the loss resistances of the excitation coil and the sensing coil, respectively. The conductivity of the measured liquid is modeled as a resistance
Rs in the circuit.
U1 represents the input voltage applied to the sensor [
19].
To obtain the output electromotive force (EMF) of the sensor, the following equation can be derived by applying Kirchhoff’s law:
Since the magnetic permeability of the sensor core is significantly higher than that of the liquid, it is reasonable to assume perfect coupling between the transformer components in the equivalent circuit model [
20,
21]. Given that the sensor operates under high-frequency conditions, it can be assumed that
R1 <<
ωL1,
R4 <<
ωL4, where
ω is the angular frequency and
L1,
L4 are the inductances of the excitation and sensing coils, respectively. Furthermore, in this study, a virtual short-circuit configuration, implemented with an operational amplifier, is used to measure the short-circuit current. Based on these assumptions, the following conditions can be derived:
In the equation,
k12 and
k34 represent the inductive coupling coefficients between the respective coils and the liquid. Therefore, the short-circuit current
I4 can be expressed as
The probe section of the inductive conductivity sensor comprises two toroidal cores, which are each independently wound with a coil. A schematic diagram of this structure is shown in
Figure 4.
In
Figure 4,
N1 represents the number of turns of the excitation coil, while
r1 and
r2 are the inner and outer radii of the toroidal magnetic core, respectively.
t denotes the thickness of the magnetic core, and
d is the distance between the excitation coil and the sensing coil. Both the excitation coil and the sensing coil have identical physical structures, meaning they share the same number of turns and the same magnetic core dimensions. The inductance
L of the toroidal coil is given by the formula in Equation (4).
In the equation, μ0 represents the permeability of free space, μr is the relative permeability of the magnetic core, and a is an inductance coefficient that depends on the dimensions and material properties of the toroidal magnetic core.
Substituting Equation (4) into (3) yields
In the equation,
k is the conductivity constant,
Gs represents the conductivity of the water,
a1 is the inductance coefficient of the excitation coil on the toroidal magnetic core, and
a4 is the inductance coefficient of the sensing coil on the toroidal magnetic core.
a2 is the inductance of the water-equivalent single-turn coil on the excitation coil’s toroidal magnetic core, and
a3 is the inductance of the water-equivalent single-turn coil on the sensing coil’s toroidal magnetic core. Since the physical structures of the excitation and sensing coils are identical, it follows that
a2 =
a3. After the short-circuit current
I4 passes through the virtual short-circuit circuit constructed with the operational amplifier, the output voltage
Uout is given by
Uout =
Rf ×
I4. Therefore, the sensor’s output can be expressed as
It can be observed that once the input signal, magnetic core coil physical structure parameters, and material properties are determined, the output of the inductive conductivity sensor shows a linear relationship with the conductivity of the measured water.