1. Introduction
The interaction between the wheel/track and soft ground directly affects the driving performance of wheeled/tracked vehicles running on soft terrain. In order to obtain a deep understanding of the interfacial characteristics between the wheel/track and soil, scholars have conducted experimental and simulation research [
1,
2,
3,
4,
5,
6] using soil bin test systems. However, the mechanical properties of snow are more complex than those of soil. Experimental studies on the interfacial performance between wheels/tracks and snow based on the soil bin system are limited because it is difficult to guarantee the snow environment, and the simulation research is limited because of the lack of a feasible snow model.
Snow is a kind of porous/multiphase material whose mechanical properties are affected by light and the water content, temperature, and crystal structure of snow. A series of mechanical tests conducted by the Cold Region Research and Engineering Laboratory [
7,
8,
9,
10,
11] (CRREL) on snow showed that the strength of the snow increased 10-fold after 6 days of sintering, and the shear index was irregularly related to the temperature and crystal size of the snow. In the density range of 900 kg/m
3, the elastic modulus of snow changes by four orders of magnitude, and the bearing capacity of the elastic part of snow on a vehicle can be ignored when the density of the snow is below 300 kg/m
3. Based on the experimental data of snow mechanical properties conducted by CREEL, Sally Shoop [
11,
12] analyzed a plastic model of snow in detail and calibrated the parameters of the snow with a density of 200 kg/m
3. Jonah H analyzed the stress distribution of snow under the interaction between wheel and snow based on the Modified Drucker–Prager Cap model [
13], and verified the theoretical model using simulation results of the interaction between wheel and snow in the absence of relevant experimental data [
14,
15]. The traction force and motion resistance of patterned tires running in snow were simulated, and the interfacial characteristics between the patterned tires and snow with different model parameters was compared by Choi, J. H [
16] using the FEM-FVM coupling simulation method.
However, the mechanical properties of snow used in the above numerical simulation are not consistent with those of actual snow. In order to reflect the mechanical properties of snow in different regions, temperatures, and sintering times, the model parameters need to be further studied and redefined. Some methods for calibrating soil parameters can be used for reference. Soil model parameters including cohesion, internal friction angle, saturation, and density need to be obtained using appropriate testing methods, such as laboratory experiments, triaxial experiments, direct shear experiments, in situ tests, and cone penetration tests. These selected methods should produce results as close as possible to the field values and provide all of the data necessary for the numerical simulation, such as continuum-based numerical techniques and discrete-based numerical techniques [
17,
18]. In order to solve the problem of slope failure, Huang and Fei made a soil cylinder sample in the laboratory and tested the shear strength of unsaturated soil through triaxial experiments [
19]. In order to calibrate the parameters of the DEM of simulated lunar soil, Jianzhong Zhu conducted conical pile experiment tests and calibrated the angle of repose. Penetration tests were conducted to verify the accuracy and validity of the DEM parameters [
20]. In order to test the interaction behavior between a small-wheeled mobile platform tire and forest soil, Liyang Yao established the FEM-DEM simulation model, in which soil parameters were obtained through standard geotechnical tests and uniaxial experiments [
21]. However, whether these methods suitable for testing soil parameters are suitable for testing snow parameters remains to be studied because of the limited bearing capacity of snow and the difficulty of obtaining snow experiment samples.
The in situ test of soft ground can maintain the mechanical properties of undisturbed soft ground as much as possible and can provide more accurate results than laboratory test results. Parameter inversion is a common method used to calibrate soft ground parameters by using in situ test results. Zhu Min conducted a parameter inversion of the relevant parameters of the hardened soil model based on a self-drilling side-pressure experiment curve, and obtained the value range of the parameters of the hardened soil model for finite element simulation analysis [
22]. The Duncan–Chang model is used to establish the finite element model of soil in the foundation cover layer. Based on the sensitivity analysis of each parameter of the model, Liu Xiaosheng took the laboratory test results as the initial values to invert the soil parameters in the foundation cover layer. Compared with the traditional laboratory soil sample test results, the parameter inversion results are closer to the in situ test results [
23]. Rangeard D. calibrated the parameters of the Cam–Clay model using the parameter inversion method [
24]. However, no investigation has been conducted into the back-analysis of snow parameters based on the in situ test results.
In addition, machine learning may also be an effective method to calibrate the parameters of soft terrain models, but the application of machine learning-based methods in the calibration of snow parameters in the area of snow thickness and temperature calibration has not been reported in the literature. For example, Yao Heming proposes a novel inverse method based on the deep convolutional neural network to extract data on the layer thickness and temperature of snow via passive microwave remote sensing [
25], and Junyu Zhan proposed a novel global navigation satellite system–interferometric reflectometry signal-to-noise ratio-retrieving snow depth method to monitor the depth of snow [
26]. Deep learning technology in the field of soil is mainly applied in soil classification, soil image processing, soil terrain recognition, etc., and is less applied in soil mechanic parameter calibration.
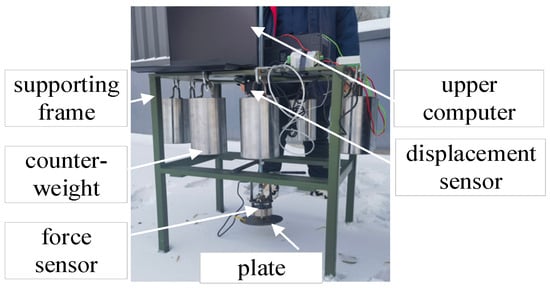
The accuracy of a snow model directly affects the simulation results of wheeled/tracked vehicle driving performance in snow. In this paper, an innovative method of parameter inversion based on in situ test results of the load–sinkage relationship of snow is proposed to calibrate snow parameters: A finite element model of plate loading was established to analyze the sensitivity of snow parameters to the load–sinkage relationship, the snow parameters with greater sensitivity were selected and calibrated based on the in-situ test results of load–sinkage relationship. Compared with the traditional experimental method for measuring the mechanical properties of soft terrain, as shown in
Table 1, the parameter inversion method proposed in this paper, which avoids the destruction of undisturbed snow when obtaining experimental samples, is more suitable for the measurement of snow parameters.
3. MDPC Snow Model
Snow is a porous polyphase material, whose plastic deformation can be simulated using the Mohr–Coulomb model, Drucker–Prager model, Modified Drucker–Prager Cap model, etc. Compared with the Mohr–Coulomb model and the Drucker–Prager model, the Modified Drucker–Prager Cap (MDPC) plastic model can more realistically simulate the plastic deformation of snow by adding a material yield criterion caused by isotropic compression. According to Ref. [
11], the yield surface of the MDPC plastic model is described by the stress invariant in the stress tensor, which can be expressed as Equations (4)–(6):
where p is the equivalent stress, q is the deviator stress, r is the third stress invariant, and S is the stress deviator tensor, where = σ + pI. The combination of the second and third stress invariants forms a new invariant expression, as in Equation (7):
where K is the stress flow potential (the ratio between the tensile stress and the compressive stress) and describes the yield surface in the deviator stress plane. When K = 1, the yield surface is circular, and the tensile yield stress and compressive yield stress are equal. When K = 0.778, the model can approximately describe the Mohr–Coulomb yield surface, as shown in Figure 2.
The yield surface of the MDPC plastic model can be expressed in the p-t plane, as shown in
Figure 3, which includes shear yield surface, Cap yield surface, and transition surface, which can be expressed by Equations (8)–(10), respectively.
where d is the material cohesion, β is the angle of friction, α is the transition surface coefficient, R is the Cap eccentricity, is the intersection point of shear yield surface and Cap yield surface, and is the hydrostatic pressure ( is a function of the volumetric plastic strain , ), which defines the hardening law during compression.
When the stress state of snow reaches the initial yield surface, it is necessary to use the stress flow potential to describe the relationship between the plastic strain increment tensor and the plastic stress increment tensor. As shown in
Figure 4, when the non-correlated plastic flow potential is applied to the shear yield surface and the correlated plastic flow potential is applied to the Cap yield surface, the stress flow potential surface can be expressed as Equation (11) and Equation (12), respectively.
4. Snow Parameter Inversion
The cohesive force, angle of friction, elastic modulus, and hardening law of the model should be calibrated based on triaxial experiments and direct shear experiments, which have been widely used in soil mechanics [
28,
31]. As for snow, its bearing capacity is limited, and its mechanical properties are greatly affected in the process of obtaining experimental samples, which leads to experimental test results that are far from the original values. Therefore, an innovative method for the parameter inversion of snow model parameters based on the in situ test results of the load–sinkage relationship of snow is proposed in this paper, as shown in
Figure 5. This method avoids the disturbance of snow during the preparation of the experimental samples, which leads to inaccurate parameter calibration results.
4.1. Simulation Model
The simulation model of circular plate loading in snow was established, and the MDPC model was used to describe the plastic deformation of snow. The plate diameter was 0.1 m and the snow depth was 0.2 m (the same as the experimental condition above). According to the relevant literature and simulation results, when the snow radius is greater than two times the circular plate radius, the snow boundary will not be deformed. Thus, the snow radius was 0.125 m.
The snow under circular plate loading will have large plastic deformation, which will cause great difficulty in the convergence of the simulation [
36]. In the simulation of the interaction between wheel and snow, Jonah H. Lee improved the mesh quality in the simulation process using the Arbitrary Lagrange–Eulerian (ALE) method [
14]. The ALE method can re-mesh the geometry when the mesh is distorted. However, the situation still exists in which the simulation process is aborted due to poor mesh quality. The wide applicability of the ALE method is limited, especially in the simulation of tracked vehicles running on snow.
The coupled Eulerian–Lagrangian (CEL) method is an effective method to solve the large deformation problem [
37,
38]. The snow material flows freely in the Euler region, and the mesh does not deform. Therefore, the Euler region of the snow was established, and the snow depth was 0.2 m, as shown in
Figure 6. The model parameters of the snow are shown in
Table 2.
The simulation process lasts for 96 s and the sinkage of the circular plate is 0.185 m (the same as in the experiment). When the circular plate moves down a certain distance, the circular plate is unloaded, and the unloading displacement is 10 mm (at this distance, the elastic deformation of the snow is completely restored, and the unloading/reloading stiffness of the snow can be calculated).
4.2. Sensitivity Analysis of Snow Parameters
The sensitivity of the snow model parameters to the load–sinkage relationship of snow was analyzed by means of a single-factor sensitivity analysis method in this paper. Taking the snow parameters in
Table 1 as the comparison group, the parameters marked with * were changed separately, with the other parameters unchanged (30%, 60%, 130%, and 160% of each variable to be changed were taken as the experimental group, with a total of 24 experimental groups). Circular plate-loading simulations were carried out on each sample to analyze the sensitivity of each variable to the load–sinkage relationship and unloading stiffness.
4.3. Parameter Inversion of Snow Model Parameters
In the process of inverting the snow parameters, the load–sinkage relationship of snow obtained from the in situ test in
Section 2.2 was used as the matching data. The model parameter closest to the experimental test result in the sensitivity analysis was taken as the initial value of the parameter inversion, the maximum correlation coefficient between the test result and the simulation result of the load–sinkage relationship was taken as the objective function, and the model parameters were searched by the NSGA-II optimization algorithm. The correlation coefficient can be expressed as Equation (13):
where X is the experimental result and Y is the simulation result. The range of the correlation coefficient R is [−1 1]. When R = 0, X and Y have no correlation; when |R| = 1, there is a linear function relationship between X and Y. When |R| < 1, the change in X will cause the change in Y. The greater the absolute value of R, the greater the change in Y caused by the change in X. When |R| > 0.8, the correlation between the two is strong.
The NSGA-II algorithm is a genetic algorithm based on the Pareto optimization concept, which includes fast non-dominated sorting, an individual crowding distance operator design, and an elite retention strategy. The NSGA-II used was set as follows: crossover probability 0.91, genetic algebra 63, initial population size 27, crossover index 10, variation distribution index 20, and a total of 1200 iterations. In the process of parameter inversion, the initial value of the model parameters is used to simulate the load–sinkage relationship, and then the objective function under the model parameters is calculated. When the objective function under the parameter is less than the given optimization termination condition, the model parameters are adjusted according to the NSGA-II optimization method, and the load–sinkage relationship under the new model parameters are re-simulated. When the objective function under this parameter is greater than the given optimization termination condition or reaches the given number of iterations, the simulation ends.
6. Conclusions
In this paper, the snow plastic model, the MDPC model, was analyzed. A simulation model of the load–sinkage relationship of snow under circular plate loading was established by using the coupled Eulerian–Lagrangian method. A single-factor sensitivity analysis of the snow parameters was carried out, and an in situ experiment of the load–sinkage relationship was conducted. The parameter inversion of the snow model parameters was carried out by using the experimental results as the matching data, and the following conclusions were obtained:
(1) In the simulation of the large deformation of soft terrain such as snow, the mesh was seriously distorted when using the Lagrange method, resulting in the simulation being aborted. The CEL method is an effective method to simulate the large deformation of snow.
(2) The material cohesive, angle of friction, and hardening law of snow have a great influence on the load–sinkage relationship during continuous loading. The elastic modulus of snow has a great influence on the unloading stiffness of snow, while the Poisson’s ratio and density have almost no influence on the bearing characteristics of snow.
(3) The parameter inversion of the snow model was carried out. The load–sinkage curve obtained by inversion had a good fit with the experimental data, and the correlation coefficient was 0.979.
(4) The simulation results of the load–sinkage relationship of snow under circular plate loading based on the snow parameters obtained by parameter inversion had a good fit with the experimental data with different plate diameters and snow depths. In the cases studied in this paper, the minimum correlation coefficient between the simulation results and the experimental results was 0.8743. The snow model parameters calibrated by parameter inversion were able to reflect the bearing characteristics of the experimental snow accurately.
In this paper, the snow parameters were inverted based on the in situ test results of the load–sinkage relationship of snow, and the simulation model of undisturbed snow was obtained. In the future, further in situ testing experiments will be conducted on the load–sinkage relationship of snow in different regions, at different depths, at different sintering times, and for different microscopic crystal structures. More experimental data will be used to verify the inversion results of the snow parameters, analyze the relationship between snow parameters and water content, temperature, light, crystal structure, etc., and build a snow parameter database. The performance of wheeled/tracked vehicles in different types of snow will be predicted by numerical simulation. Moreover, deep learning technology may have broad application prospects in the research of snow, including model parameter calibration, and will be very helpful in solving the existing key technical problems.