Greenberg News

    Green Futures: Innovate, Sustain, Thrive

    Strategies for Multigeneration in Residential Energy Systems: An Optimization Approach

    Greenberg     January 27, 2025 in News - 7 Minutes


    2.1. Energy Demands

    The case study focuses on a 30-story residential building located in João Pessoa, Northeast Brazil. The building’s energy demands include electricity, hot water, and cooling (air conditioning). The characterization of electricity demands was conducted following the Brazilian standard ABNT NBR 5410:2004 [20], which specifies lighting loads based on room area, electrical outlet dimensions based on the room perimeter, and active power requirements for equipment such as elevators, pool pumps, and water reservoirs. Demand factors were applied in accordance with the guidelines of the local electricity utility [21]. Hot water demands were determined based on the daily useful energy requirements (kWh/day), following Brazilian standard ABNT NBR 15569:2021 [22]. Cooling loads were estimated using the degree-day method [23], assuming daily air-conditioning usage in apartment units from 9 pm to 7 am (on both weekdays and weekends). The reception area (front desk) maintained 24 h air-conditioning operation, while the party room required cooling only between 4 p.m. and 10 p.m. on weekends. An electric vehicle charging station was also included in the analysis, operating 24 h a day with the capacity to charge two vehicles simultaneously, twice daily, at a rate of 22 kW per charge.

    The analysis was conducted using two representative days per month: one for weekdays and one for weekends/holidays. Each day was divided into 24-hourly periods, resulting in a total of 576 hourly periods. The building’s annual energy demands were calculated as 747.74 MWh/year for electricity, 330.34 MWh/year for hot water, and 85.37 MWh/year for cooling.

    2.2. Superstructure and Equipment Specification

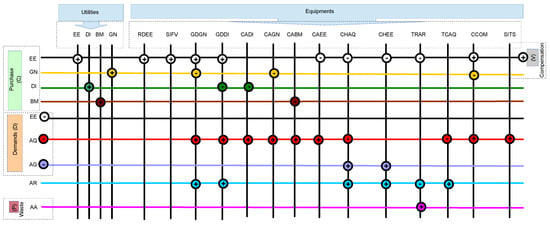
    The superstructure includes all possible technologies, available energy resources, and their interactions. Equipment is included in the superstructure based on the energy demands of the residential building, considering commercially available technologies. Figure 1 illustrates the superstructure considered herein. A positive node indicates energy production (supply), and a negative node indicates consumption. Horizontal lines refer to physical distribution systems into which the equipment (the vertical lines) can supply or consume.
    On the left side of Figure 1, the green box indicates the energy resources available for purchase. For example, EE is Electricity, which can be produced (+) or consumed (−) by equipment. Also, on the left side of Figure 1, the orange box indicates the energy demands of the building. The upper section of Figure 1 shows the available resources and equipment. Electricity generated by the PV system can be exported to the electric grid, following Brazilian law [19]. Table 1 and Table 2 summarize the utilities and technologies available on site.
    Technical parameters of the equipment were obtained from equipment data sheets and are displayed in Table 3, along with costs. Appendix A presents detailed equipment data. Capital costs were obtained from consultation with manufacturers, and operation and maintenance (O&M) costs were obtained from the Brazilian National Research System on Civil Construction Costs and Indices [24].
    Direct price surveys were carried out to obtain the tariffs for the energy services. The location used as a reference for the case study was the city of João Pessoa. For biomass (sugarcane bagasse), the value of Delgado et al. [25] was used (BRL 78/MWh), and, for diesel, the value used was BRL 743.46/MWh [26].
    The electricity tariff for the residential consumer unit is BRL 356.61/MWh, a conventional flat tariff throughout the day [27]. For natural gas, the tariff is BRL 451.38/MWh [28], which is also a flat tariff.

    2.3. Modeling and Programming

    The model was implemented using C++, a high-performance programming language chosen for its ability to handle complex calculations and large data volumes efficiently, as the proposed problem requires. In energy optimization, using C++ offers advantages such as enabling the development of customized algorithms and direct integration with optimization libraries like CPLEX, facilitating the resolution of highly complex problems.

    The flowchart in Figure 2 presents the required steps and the sequence of the modeling of the multigeneration system, as well as the requirements for programming and optimization.
    IBM® ILOG® CPLEX® Optimization Studio v20.1 [29] was employed, a decision optimization software for building and solving complex optimization models. The solution provides the results of an economic analysis, specifying the optimal configuration, including the type and quantity of equipment to install, as well as the operational strategy required to achieve minimal annual costs. All input data were organized into spreadsheets, with separate sheets for energy demand, a list of technical coefficients, investment, maintenance, and operational costs, and a third sheet for tariff information.
    The economic objective function is the minimization of total annual costs (Ctotal), comprising fixed annual costs (Cfix, capital costs) and variable costs (Cvar), which include the costs of purchasing of energy resources and O&M costs, as shown in Equations (1)–(3).

    Min   C total =   C fix + C var

    C fix = [ frc · 1 + fci · ∑ t ∈ T i t y t ] + SisFV + SisTS

    C var = ∑ m ∈ M ∑ r ∈ R ∑ h ∈ H ∑ t ∈ T ( c t x mrht + cm t   x mrht ) − ∑ m ∈ M ∑ r ∈ R ∑ h ∈ H ∑ t ∈ T ∑ n ∈ N c n Q mrhnt

    The fixed costs consider the capital recovery factor (frc = 0.13) and an indirect cost factor (fci = 0.15). i refers to the capital cost and y to the number of installed equipment. t is the type of equipment. SisFV and SisTS refer to the capital costs of the solar PV and thermal systems.

    Within the variable costs, m, r, and h refer to, respectively, month, representative day, and hour. ct refers to the cost of technology t in reais (Brazilian currency), and xmrht indicates the use of technology t during month m, day r, and hour h (measured in hours). cm t   is the cost of technology maintenance cost t in reais (Brazilian currency), and Qmrhnt is the excess of utility n used by technology i during month m, day r, and hour h (measured in hours).

    The operational limits of the system are implemented as restrictions in production, capacity, and energy balance equations. For each time period, energy production is restricted to the installed capacity, and an energy balance must be followed for each utility n, as shown in Equation (4).

    S mrhn + P mrhn −   E mrhn −   C mrhn −   D mrhn −   W mrhn = 0

    In Equation (4), S, P, E, C, D, and W represent Purchase, Production, Excess, Consumption, Demand, and Waste, respectively, for utility n in month m, day r, and time h.

    The restriction expressed by Equation (5) guarantees that all energy demands are met because production must be greater than the sum of demand and consumption. A tn indicates the production of utility n by technology t.

    ∑ t ∈ T x mrht A tn ≥ D mrhn + C mrhn ,   ∀ m ∈ M ,   ∀ r ∈ R , ∀ h ∈ H ,   ∀ n ∈ N   e   ∀ t ∈ T

    The restriction shown in Equation (6) indicates that the excess of a utility in a specific hour is the difference between the production and consumption of equipment.

    ∑ t ∈ T x mrht A tn − D mrhn + C mrhn = E mrhn ,   ∀ m ∈ M , ∀ r ∈ R , ∀ h ∈ H ,   ∀ n ∈ N   e   ∀ t ∈ T

    Equation (7) guarantees that the total amount of an internally used utility (consumption and demand) cannot be higher than the excess produced. Q mrhnt indicates the used excess of utility n in month m, day r, and hour h by technology i.

    ∑ t ∈ T Q mrhnt ≤ E mrhn ,   ∀ m ∈ M ,   ∀ r ∈ R , ∀ h ∈ H ,   ∀ n ∈ N   e   ∀ t ∈ T

    Equation (8) limits the excess used by a piece of equipment. U nt is how much, proportionally, technology t uses of n.

    Q mrhnt ≤ U nt x mrht ,   ∀ m ∈ M ,   ∀ r ∈ R , ∀ h ∈ H ,   ∀ n ∈ N   e   ∀ t ∈ T

    Equation (9) indicates that the maximum number of equipment installed must be equal or higher than the amount of equipment used at any time. Y t is the maximum amount of technology t used.

    Y t − x mrht ≥ 0   ,   ∀ m ∈ M ,   ∀ r ∈ R , ∀ h ∈ H ,   e   ∀ t ∈ T

    The restrictions shown in Equations (10)–(14) define the nature of the decision variables.

    x mrht ≥ 0 ,   ∀ m ∈ M , ∀ r ∈ R , ∀ h ∈ H ,   e   ∀ t ∈ T

    E mrhn ≥ 0 ,   ∀ m ∈ M ,   ∀ r ∈ R , ∀ h ∈ H   e   ∀ n ∈ N

    Q mrhnt ≥ 0 ,   ∀ m ∈ M ,   ∀ r ∈ R , ∀ h ∈ H   e   ∀ n ∈ N   ∀ t ∈ T

    Y t ≥ 0 ,   ∀ t ∈ T

    Y t ∈ Z ,   ∀ t ∈ T



    Source link

    Danielle Bandeira Mello Delgado www.mdpi.com

    Related Posts

    JMSE, Vol. 13, Pages 249: Navigating Uncertainty: A Novel Framework for Assessing Barriers to Blockchain Adoption in Freeport Operations
    January 29, 2025
    Climate change primed LA to burn — catastrophically
    January 29, 2025
    Environmental Factor – May 2021: Environmentally persistent free radicals may affect lung health
    January 29, 2025

    Greenberg

    Learn More →
    This website uses cookies to improve user experience. By continuing to use the site, you consent to the use of cookies.