The production of green hydrogen can be defined as a process which generates hydrogen based on some renewable source such as wind, solar, or biomass energy [1]. In this way, green hydrogen can be considered a clean method of producing hydrogen which will emit less carbon dioxide than grey hydrogen, which is based on using fossil fuels [1]. One promising method for producing green hydrogen is through electrolysis, where water is split to generate hydrogen and oxygen [2]. In particular, this is an attractive option if the energy used to drive electrolysis is obtained from renewable sources. For example, Hosseini et al. consider electrolysis driven by either wind or solar power as a clean method for producing hydrogen [3]. However, they also mention that one of the limitations of electrolysis is the high costs of the rare metals used in the electrodes [3]. A comparison of the costs of producing hydrogen showed that green hydrogen combined with renewable energy might cost between 2.28 and 7.39 $/kg while grey hydrogen from methane or coal might cost 0.67–1.31 $/kg [4]. Hence, there is a drive to make electrolysis systems cheaper and more efficient at producing hydrogen to make them more competitive. Discussion and comparisons of the different methods for producing hydrogen can also be found in the reviews of Acar and Dincer as well as Dash et al. [5,6]. Furthermore, life cycle analysis has also been carried out for different hydrogen production methods [7,8]. In both these studies, the environmental impacts of hydrogen production through electrolysis are compared with different energy sources, and both find electrolysis powered by renewable sources such as wind and solar are the most beneficial [7,8]. Recently, there has also been growing interest in using algae to produce hydrogen [9].

A large number of studies and reviews have investigated how to improve hydrogen production through electrolysis of water. The review of Wang et al. looks in detail at different amorphous materials that can be used as electro-catalysts for water splitting [10]. Olivier et al. review and discuss the modelling and model equations required, including different analytical and empirical relations used [11]. Hu et al. also reviews modelling approaches focusing on alkaline water electrolysis [12]. In addition to giving model equations, they also discuss the importance of different operating conditions such as temperature, pressure, electrolyte flow, and concentration [12]. They also list a range of different ways by which water electrolysis can be enhanced, including modifying operating conditions, changing the design/geometry of the electrolyzer, using different catalysts, and applying external fields (gravity, magnetic, ultrasound, and pulsing electric fields) [12].

The review of Li et al. goes into great depth discussing the theory and mechanisms by which magnetic fields can enhance water electrolysis [13]. They mention the following three main effects [13]:

Most recently, Sun et al. have also discussed these effects and some of the latest results that have been obtained from applying magnetic fields to water electrolysis [14]. Both of these reviews provide detailed discussion of the theory and provided examples from the literature where magnetic fields have provided some enhancement [13,14]. However, they have offered only limited comparisons of the different enhancements obtained by these methods [13,14]. In most cases, the enhancements are discussed separately for each existing study and attributed to one of the three main effects mentioned above. In addition, both Sun et al. and Li et al. point out that there may be multiple effects in play when applying a magnetic field, so it is difficult to assess the combined effects, requiring further study [13,14].

Section 2 gives basic details about the design and modelling of electrolysis systems, highlighting inefficiencies/limitations. Section 3 examines the empirical performance of enhancements through the application of external magnetic fields, and Section 4 discusses the limitations of existing work in this field and gives recommendations for future research in the area of magnetic field-assisted water electrolysis.

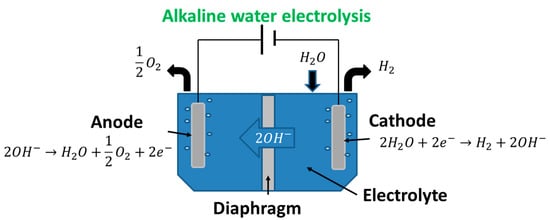
Water electrolysis systems are all based on the water splitting reaction as shown in Equation (1). This overall reaction relies on electrons being transferred through an electric circuit from the anode to the cathode. However, the reactions which occur at the anode and cathode depend on the type of electrolysis system, with one of the common designs and the associated reactions shown in Figure 1. This type of electrolysis is defined as one of the “mature” methods in terms of technological readiness [15]. In this review, the focus is on enhancing the most mature existing technology, which is alkaline electrolysis.

The energy for water splitting (shown in Equation (1)) is provided by the voltage applied. The Gibbs free energy $\left(∆G\right)$ of this overall reaction is related to the reversible voltage $V_{rev}$ as defined by Equation (2) [16]:
where z is the number of electrons transferred and F is the Faraday constant [16]. The Gibbs free energy depends on the operating temperature and pressure [17]. Correlations are available for predicting this where it can be seen that $V_{rev}$ reduces with increasing temperature [12]. However, the actual voltage used for the electrolysis cell $V_{cell}$ must be higher than this for a number of reasons. Firstly, there will be an irreversible change in entropy $\left(∆S\right)$ such that voltage is increased to

where $∆H$ is the change in enthalpy related to Gibbs free energy through $\left(∆G=∆H-T∆S\right)$ and $V_{tn}$ is the thermoneutral cell voltage [16]. In addition to this, the voltage must be increased further to account for various resistances in the system. These resistances translate to increases in the voltage called overpotentials. Figure 2 shows a typical voltage–current density diagram which shows how voltage changes increase current density.

The overpotential can be broken down into ohmic overpotentials (related to factors such as electrolyte concentration, electrode gap, bubble coverage on electrodes, temperature, and pressure) and activation overpotentials (related to factors such as electrode materials, bubble coverage, and current density) as well as diffusion overpotentials [12]. Combining all these terms, the overall cell voltage can be calculated by Equation (4) [12]:

where $V_{act,c}$ and $V_{act,a}$ are the activation overpotentials of the cathode and anode, which may have different electro catalyst materials, $V_{Ohm}$ is the ohmic overpotential, and $V_{diff}$ is the diffusion overpotential. While detailed analytical models are available for estimating the separate parts of the overpotential, there are also empirical models for estimating the overall overpotential [11].

The hydrogen production rate $\left({\dot{n}}_{H_2}\right)$ can be obtained using Faraday’s law as shown in Equation (5) [11]. This says that the hydrogen production is proportional to the current flowing through the system $\left(I\right)$.

However, due to current losses in the system, sometimes called parasitic losses, it may not be possible to convert 100% of the current supplied into hydrogen production [10]. To account for this difference, the Faraday efficiency ${\eta }_F$ can be inserted into Equation (5) to give Equation (6) [16]. Hence, Equation (6) can be used to calculate the hydrogen production from a single electrolysis cell (multiplying by the number of cells to give the total hydrogen production [16]. For alkaline electrolysers the Faraday efficiency can be calculated through empirical correlations [11].

Both of these affect the overall energy efficiency of hydrogen production through electrolysis. Typically, when attempting to improve efficiency, research to reduce overpotentials focuses either on overpotentials associated with the hydrogen evolution reaction (HER) at the cathode or the oxygen evolution reaction (OER) at the anode [18].