1. Introduction
ULF waves serve as important links between the solar wind, magnetosphere, and ionosphere, and their study continues to reveal insights into space physics, geospace dynamics, and planetary environments. ULF waves can propagate along and across magnetic field lines (depending on their modes and characteristics) within the magnetosphere and interact with field-aligned currents (FACs). Field line resonances (FLRs) occur when these waves resonate with specific field line configurations, leading to enhanced energy exchange between the magnetosphere and ionosphere. The energy carried by ULF waves can modulate FACs, facilitating the transfer of energy from the magnetosphere to the ionosphere (e.g., [
1]). Solar wind forcing, such as interplanetary shocks and dynamic pressure pulses, significantly impacts Earth’s magnetosphere, leading to the production of electromagnetic waves, plasma heating, and energetic particle acceleration. The magnetospheric response involves immediate plasma heating and particle acceleration, lasting for several hours. Even small changes in solar wind pressure can generate waves, including poloidal-mode ultra-low-frequency (ULF) waves.
ULF waves also interact with charged particles in the radiation belts and the ring current (e.g., [
2,
3,
4,
5]). Resonant interactions lead to radial diffusion, drift motions, pitch-angle scattering, and particle precipitation. ULF waves can modulate chorus and hiss emissions, affecting the loss and acceleration of radiation belt electrons. These interactions play a role in radiation belt dynamics and space weather effects. ULF waves are energized by the solar wind as it interacts with the Earth’s bow shock and magnetosheath.
The acceleration of energetic electrons in the radiation belt and ions in the ring current region occurs in two stages: initial adiabatic acceleration due to magnetospheric compression, followed by wave–particle resonant acceleration driven by global or localized poloidal ULF waves. A generalized theory of drift and drift–bounce resonance with localized ULF waves explains the observed features such as distorted energy spectra and unique pitch angle distributions. Poloidal ULF waves are particularly effective at accelerating and modulating radiation belt electrons and ring current ions (e.g., [
6]). These findings are applicable to solar wind interactions with other planetary magnetospheres and astrophysical objects with magnetic fields.
Solar wind compressions and expansions generate ULF wave activity in the foreshock region. Alfvén/ion cyclotron waves and mirror modes in the magnetosheath contribute to ULF wave generation ([
7,
8,
9]). The presence of these modes affects wave properties and propagation. These waves are more prevalent when the interplanetary magnetic field (IMF) is nearly radial (aligned with the Sun–Earth line), as this condition enhances wave coupling and energy transfer.
Understanding the intricate plasma dynamics of Earth’s magnetosphere requires an understanding of the turbulence and waves in the foreshock and magnetosheath regions ([
10]). These areas are important for the study of particle acceleration, energy transmission, and dissipation in space plasmas. Research on these complex systems is still ongoing, utilising both theoretical models and observational data. Several research outcomes have had an impact on our comprehension of space weather and the larger field of astrophysics. The universe is full of magnetised plasma waves, which are expected to be significant in many different astrophysical environments. Many attempts have been made to derive effective wave mode descriptions of plasma dynamics, speculating that turbulence may be a leading factor, characterised as an ensemble of waves. Critical balance predicts an isotropic cascade of energy in wave vector space, where magnetic energy cascades at varying rates, parallel and perpendicular to the local mean magnetic field. The theory of critical balance can be extended to smaller scales than that of the ion gyroradius, at which wave–particle damping and collisions become significant, even though the initial predictions only applied to a cascade of Alfvén waves in the magnetohydrodynamic (MHD) limit of the inertial range.
With frequencies ranging from 0.001 to 5 Hz, ultra-low frequency (ULF) waves are the lowest frequency plasma waves in the Earth’s magnetosphere [
11], frequently observed in planetary foreshocks [
12]. Waves at the lower end of the ULF band include eigenmodes with wavelengths comparable to the magnetosphere’s size, and they are frequently well-described using an MHD approximation. Approaching the ion-cyclotron frequency, ULF waves are better described by other approximations (e.g., local linear kinetic theory [
13]). The magnetosphere–ionosphere (MI) coupling, ring current/radiation belt dynamics ([
14,
15,
16]), modulation of very low frequency (VLF) waves/precipitation ([
17,
18,
19]), geomagnetically induced currents (GIC) [
20], substorms ([
21,
22,
23]), and other areas relevant to space weather prediction are all impacted by ULF waves.
Research on nonlinear whistler waves has been of great interest in regards to laboratory ([
24,
25]) and astrophysical ([
26]) plasmas. Specifically, it is well known ([
27,
28,
29,
30,
31]) that modulational instability of a large amplitude whistler wave can occur in response to ion-acoustic disturbances and MHD. The modulated whistler wave’s dynamics are controlled by a nonlinear Schrödinger equation. The nonlinearity emerges later as the whistler wave packet links with low-frequency density perturbations. The whistler wave packet is finally localised as envelope solitons in the final stage due to these unstable modulations ([
26,
30,
31]). In reality, in both lab studies and in the upstream direction of the solar wind, the whistler wave localisation (envelope soliton) has been observed. However, the spectrum of the weakly interacting waves cannot be pushed into a single coherent wave when the whistler waves are insufficiently strong [
32]. The weak turbulence theory ([
32,
33]) should thus be used to treat the dynamics of whistler waves with modest amplitudes. Ref. [
34] have demonstrated that randomly phased small amplitude plasmons can become modulationally unstable for an unmagnetised plasma. Many forms of low-frequency disturbances arise in magnetically confined plasmas, and they may nonlinearly link with whistler waves. Therefore, the fast magneto-sound and ion-sound perturbations that modulate stationary whistler turbulence were taken into consideration ([
31]). Unstable ULF perturbations along and oblique to the external magnetic field were demonstrated. The issue of ULF emission excitation in the magnetosphere (e.g., [
35,
36]) and in laboratory investigations ([
24]) may be affected by these findings.
Ground-based magnetometers and satellite measurements provide valuable data on ULF wave characteristics, including frequency, polarization, and spatial distribution. ULF waves serve as diagnostic tools for studying magnetospheric properties and monitoring energy flow.
A number of solar system planetary foreshocks have been linked to ULF electromagnetic plasma waves connected to backstreaming protons (e.g., [
37,
38,
39,
40,
41,
42,
43,
44,
45,
46]). The interaction of reflected ions with the solar wind causes waves to be produced in the foreshock. These waves have the potential to travel upstream into the solar wind or back towards the bow shock. The entire dynamics of the region can be affected by these waves, as they can mediate the transfer of energy and momentum between the solar wind and the foreshock plasma. Particles can accelerate due to wave–particle interactions and Fermi acceleration caused by waves in the foreshock. The plasma environment around Mercury is distinct from that of other solar systems due to its small but significant Alfvén Mach number of the solar wind, which allows for the production of a foreshock. Furthermore, its orbit’s wide range of heliocentric distances makes it possible to investigate the variability of wave occurrence in a way that is not feasible anywhere else in the solar system, unless we apply a comparative planetology method. It is worth mentioning that despite all these important factors, statistical research on ULF waves surrounding Mercury has only recently begun (e.g., [
47,
48,
49]). The first comprehensive study on SLAMS at Saturn has been published by [
50].
Our review does not aim to provide a comprehensive review of space-related ULF wave phenomena in general; rather, it focuses on these waves generated in the planetary foreshock regions and their related, coupled processes observed in the planetary magnetospheres. ULF waves have already been observed on other planets as well, with more detailed, recent analyses regarding Mercury and Saturn. At Mercury, several statistical investigations regarding these waves, their distribution over the magnetosphere, and global modelling efforts have been conducted to better understand their important role in the coupling processes between the solar wind the magnetosphere in general. Comparative studies between the much better studied terrestrial plasma environment and the new results obtained in these recently investigated planetary environments are crucial for our understanding of the different factors that govern these processes; we can also apply this knowledge to exoplanetary research in the future.
First, we discuss the observations and physical processes leading to ULF-wave generation in the foreshock and transmission through the magnetosphere in the terrestrial plasma environment. We then summarize the most recent results related to ULF-wave observations and associated phenomena in the vicinity of Mercury, with a further outlook to other planets as well.
2. Foreshock Ion Populations
The Earth’s extended magnetic field, the terrestrial magnetosphere, represents an obstacle to solar wind. Since the solar wind is supersonic, or more precisely, a super-fast-magnetosonic flow [
51], when solar wind reaches the terrestrial magnetosphere, bow shock, a permanent shock wave, is formed in front of the magnetosphere. At the bow shock, the fast solar wind is slowed down to sub-fast magnetosonic speed; as it becomes compressed, the density and the magnetic field value increase, and the solar wind becomes thermalised. In other words, energy dissipation takes place. The terrestrial bow shock, but also the planetary bow shocks in general, have a curved shape that defines the local plasma environment and its properties. The average angle between the direction of the upstream interplanetary magnetic field (IMF) and the bow shock surface normal is marked as
ϑBn. According to the
ϑBn value, the bow shock can be divided into two main regions: quasi-perpendicular (when
ϑBn > 45°) and quasi-parallel (when
ϑBn < 45°). On the quasi-perpendicular side, the shock transition from upstream to downstream presents a clean, narrow, well defined transition zone, which is represented by a sharp increase in magnetic field and density value, while the bulk velocity of the plasma is decreased to a sub-fast magnetosonic value. At the same time, the initial beam-like solar wind particle energy distribution spectra is transformed into a thermalised distribution. On the other hand, the quasi-parallel side of the bow shock presents rather different characteristics: the shock transition is far less well defined and presents an extended transition zone that stretches out far upstream from the shock front. This transition zone is called the
foreshock and is dominated by waves of many types, along with energised particles.
Due to the curved shape of the bow shock, both quasi-perpendicular and quasi-parallel regions are present at the same time. The presence of a foreshock can be easily explained by taking into consideration the IMF direction. Solar wind particles (electrons and ions) that are reflected or escaping the shock front can propagate in the upstream direction along the magnetic field lines due to the low ϑBn value. These particles interact with the incoming solar wind particles through multiple physical processes and are capable of generating waves leading to an extended, turbulent foreshock region. The “turbulent” indicator in the literature is mostly used to characterize the quasi-parallel upstream bow shock region, i.e., the foreshock, compared to the quieter region upstream of the quasi-perpendicular bow shock.
The boundary of the quasi-parallel and quasi-perpendicular regions was determined more precisely, considering the aberration (the deviation of the axis of rotational symmetry of the bow shock from the Sun–Earth axis determined by the speed of the Earth’s rotation and the speed of the solar wind) and non-specular nature of the ion reflection as a field-aligned surface connected to the bow shock, where the local
ϑBn ≈ 51° [
52]. The aberration alone was found to be responsible for a 1.5–7° (on average, approximately 4°) deviation from 45°, i.e., the solar wind reaches the magnetosphere eastward of the subsolar point, and the entire magnetosphere also turns to the east by this amount.
Figure 1.
The regions in front of the terrestrial bow shock: EF, electron foreshock; IF, ion foreshock (From [
53]).
Figure 1.
The regions in front of the terrestrial bow shock: EF, electron foreshock; IF, ion foreshock (From [
53]).
There is a clear distinction between the two foreshock regions (see
Figure 1). The boundary of the electron foreshock is defined by an electron beam consisting of backstreaming electrons that are reflected at
ϑBn = 90° from the shock front. The ion foreshock is the region connected by magnetic field lines to the bow shock and thus, accessible to protons leaving the bow shock. The ion foreshock boundary is characterised by a backstreaming ion beam ([
54,
55]) that consists of reflected ions. Due to the
E ×
B drift, with
E = −
vsw ×
Bimf, deflecting the ions from their field-aligned path, the ion foreshock boundary is somewhat earthward of the interplanetary magnetic field lines tangent to the bow shock, originating at the shock front, where the
ϑBn value is about 62–67° [
56]. Thus, both the electron and the ion beam are originating from the quasi-perpendicular side of the bow shock surface. Using observations of the ISEE satellites, the ULF foreshock boundary was found to start at
ϑBn ≈ 50° on the terrestrial bow shock [
57] and at
ϑBn ≈ 45° at Saturn [
58] via Cassini.
Three distinct ion distributions were identified within the ion foreshock [
59]. The highly collimated, high-speed (~10
vA) but tenuous (~1% of the solar wind density) ion beams [
60], called the “field-aligned beams” or FABs (sometimes referred to simply as reflected ions) are aligned along the ion–foreshock boundary ([
55,
61,
62,
63]). No ULF low-frequency waves directly associated with these ion beams have been observed. It has been shown by [
55] that while convected deeper into the foreshock, the backstreaming FAB ion population interacts with upstream waves, and as a consequence, the initially highly collimated beam can be pitch-angle scattered, resulting in an “intermediate” (kidney-shaped) ion velocity distribution, showing characteristics of a low-degree pitch angle scattering ([
64,
65]) demonstrated that this intermediate ion population can be further scattered in the pitch angle, leading to the so-called “toroidally gyrating ion” population. These backstreaming beams can be regarded as a very important factor in providing free energy for the generation of ULF waves in the foreshock region ([
66,
67]).
Deeper in the foreshock, where the conditions are quasi-parallel, the phase space density of the ions becomes more diffuse. While the energy density of the beam population is concentrated in its kinetic energy (~70%), 80% of the energy of the diffuse ions is thermal energy [
60]. The diffuse ions possess energies high above the energy of the initial solar wind ions, and display a highly isotropic, doughnut-shaped distribution in velocity space [
55]. It has been shown, based on a statistical study, that the diffuse ion partial density decreases exponentially along the magnetic field lines in the upstream direction from the shock front [
68], while the steepness of the exponential is a function of the diffuse ion energy (at higher energies, the steepness of the exponential becomes lower). This behaviour of the diffuse ions shows that these ions are accelerated at the shock through a first-order Fermi acceleration or the diffusive shock acceleration (DSA) mechanism. Ref. [
67] performed the first determination of the diffuse ion exponential profile properties based on multi-spacecraft simultaneous Cluster measurements, while [
69] extended the analysis to higher diffuse ion energies. Low-frequency quasi-monochromatic waves were found [
70] to be coexisting with the intermediate and diffuse ion distributions. ULF waves become stronger, more irregular [
70], more compressional, and more linearly polarised as the spacecraft travels even deeper into the ULF foreshock. In the meantime, the peak of the ULF wave power spectrum becomes broader [
71]. In the area closest to the bow shock, highly compressive mini-shock-like wave packets, the so-called shocklets, are observed [
59].
Ref. [
72] presented the first remote-sensing global images of ion energization in the Earth’s foreshock, obtained by the Interstellar Boundary Explorer (IBEX). Their results provide insights into the ion energization process and its dependence on the bow shock obliquity. Ref. [
51] discussed the impact of reflected ions on the microstructures of the shock front in the terrestrial foreshock, with a particular focus on the Mach regime of the solar wind. The study highlights how variations in the Mach number influence the formation and characteristics of shock waves, the reflection of ions, and the generation of wave phenomena. The findings provide valuable insights into the dynamics of the foreshock and its interactions with the Earth’s magnetosphere.
In summary, there are two main sources of energies that feed the generation of waves in the foreshock region: 1. the beams produced by reflection at the quasi-perpendicular side of the bow shock, and 2. the diffuse ions produced at the quasi-parallel side of the bow shock. These two sources can be regarded as free energy sources for the generation of upstream waves. While these two sources can be regarded as independent sources, in certain circumstances they can interact in the complex foreshock system. Refs. [
73,
74] presented case studies in which the FAB generated waves influence the scattering of diffuse ions, leading to an enhanced, more effective first-order Fermi or DSA acceleration of the diffuse ions.
3. ULF-Wave Generation in the Foreshock
The ULF foreshock is embedded in the ion foreshock, and its boundary was found to be well-defined whenever
ϑBx < 45° [
57]. The ULF foreshock boundary [
75] corresponds to a guiding centre trajectory of reflected proton beams of a speed of ~1.4
vsw along
Bimf [
57]. The 45° threshold value is near the average Parker angle at Earth; consequently, the ULF foreshock is typically well-defined.
In the region where the solar wind interacts with the Earth, a specific group of foreshock low-frequency (below the ion-cyclotron frequency) ULF waves appears, with periods typically around 30 s (sometimes referred to as 30-s waves). These waves are generated via wave–particle interactions, driven by solar wind protons backstreaming from the bow shock. Energy transfer between the protons and the waves takes place whenever the Doppler-shifted wave frequency is equal to
n times the cyclotron frequency, where
n is a non-zero integer (
n = 0 corresponds to the Landau resonance). In such a case, the protons and the wave can exchange energy. The resonance condition is
where is the proton cyclotron frequency, e is the elementary charge, mp is the proton mass, Bimf is the magnitude of the interplanetary magnetic field (Bimf), ωsw is the wave angular frequency in the solar wind plasma frame, k is the wave vector, and vb is the bulk velocity of the reflected protons. According to [76], the most unstable mode is the fundamental resonance on the right-hand side when n = −1. In this case, the protons overtake the wave that propagates upstream and sense the inherently left-hand cyclotron wave electric field, with reversed polarisation. This instability was termed the ion–ion right-hand resonance [76], or the anomalous ion cyclotron resonance [77].
Considering that the backstreaming protons are guided by the interplanetary field lines, and that
vph = ωsw/
k, Equation (1) can be also written as follows:
where ϑkB is the angle between the wave vector k and the Bimf. We assume that in the plasma rest frame (i.e., the solar wind frame), the generated waves propagate upstream with the Alfvén speed along the magnetic field lines. However, the typically super-Alfvenic solar wind sweeps back the waves toward the Earth. Hence, an observer fixed in the Earth’s reference frame detects them Doppler-shifted, with a reversed sense of polarisation (i.e., as left-handed). The Doppler-shifted wave frequency can be written as follows:
where vsw is the solar wind speed. Combining Equations (2) and (3) gives the following:
where we assume that the solar wind flow is directed into the –x direction (i.e., Earthward along the Sun–Earth line), and ϑkx = π − ϑkv, is the angle between the wave vector and the x-axis. Provided that the waves propagate upstream along the field lines, i.e., k ‖ Bimf, with the Alfvén speed, Equation (4) can be further simplified as follows:
where MA = vsw/vA is the Alfvén Mach number, with vA as the Alfvén speed, and ϑBx is the angle between the Sun–Earth line and Bimf, also called the cone angle. Using typical values (the proton’s specific charge e/mp = 9.58 · 107 C/kg, MA ≈ 8, and ϑBx = 35°, Equation (5) yields the following:
For example, in this approximation, the frequency observed in a reference frame fixed to the Earth is directly proportional to the magnitude of the interplanetary magnetic field.
Moreover, based on the work of [
78], the guiding centre speed (
vb) of the protons reflected from the bow shock nose [
79] is as follows:
Substituting (6) into (5) yields the following:
and the following for typical
MA:
Both of the above approximations [
79] are also valid for satellites which have a negligible speed (few km/s) compared to
vsw upstream of the bow shock nose, and they are in accordance with the frequent observations of the 30 s waves under typical solar wind conditions, with
Bimf ≈ 5 nT. Recent kinetic simulations were successful in reconstructing many characteristics of foreshock ULF waves (e.g., [
80,
81].
Somewhat contradicting this theory, according to which the wave growth maximises parallel to the magnetic field, it was found that upstream ULF waves seem to favour a slightly oblique (typically ~20°) propagation angle ([
59,
82,
83,
84,
85,
86] suggested wave refraction as a possible explanation. This scenario was confirmed by [
85].
4. Steepening into SLAMs
The formation of a Short Large-Amplitude Magnetic Structure (SLAMS) is believed to result from the steepening of long-wavelength magnetosonic waves in the upstream region, triggered by backstreaming solar ions associated with high-amplitude, nonlinear, compressive ULF waves in the quasi-parallel upstream region [
87]. These waves, often originating from ion beam instabilities due to interactions between backstreaming particles and the incoming solar wind ([
88,
89,
90]), dominate the foreshock region. Various waves within the same frequency range within the foreshock can be generated by ring, ring-beam, and diffuse distributions [
91].
During the steepening process, a whistler wave can be generated from the leading edge of the SLAMS, detaching and behaving like a new shock front [
87]. This whistler causes a sudden change in amplitude and polarization. Initially, SLAMS propagate Sunward, but are convected back toward the bow shock by the solar wind plasma [
92]. Evolved SLAM structures move at approximately the same velocity as the ambient plasma until near the bow shock, where they contribute to shock reformation.
SLAMS, as fast-mode structures, reflect particles and contribute to continuous shock reformation at high Mach number supercritical shocks [
93]. The characteristic length of shock reformation is a few ion gyroradii, forming a foot region characterized by variable magnetic field magnitude and high plasma density ([
87,
94]). For quasi-parallel shocks, SLAMS may deflect particle beams and contribute to plasma thermalization and deceleration [
95]. The quasi-parallel bow shock can be seen as a patchwork of SLAMS, constituting an extended transition region, with variously shaped SLAMS phases rather than a single surface.
SLAMS have been detected near Earth via the CLUSTER probes ([
96,
97,
98,
99,
100]) upstream of quasi-parallel bow shocks within the transition zones. The CLUSTER mission, consisting of four spacecraft in a tetrahedral formation, provides significant advantages (compared to single-spacecraft observations) for observing ULF waves and SLAMS, as high temporal resolution measurement of spatial variations of the magnetic field and plasma environment is possible. This allows for the precise measurement of transient features—like SLAMS—and their dynamics. An example of SLAMS observations upstream of the quasi-parallel bow shock is shown in
Figure 2.
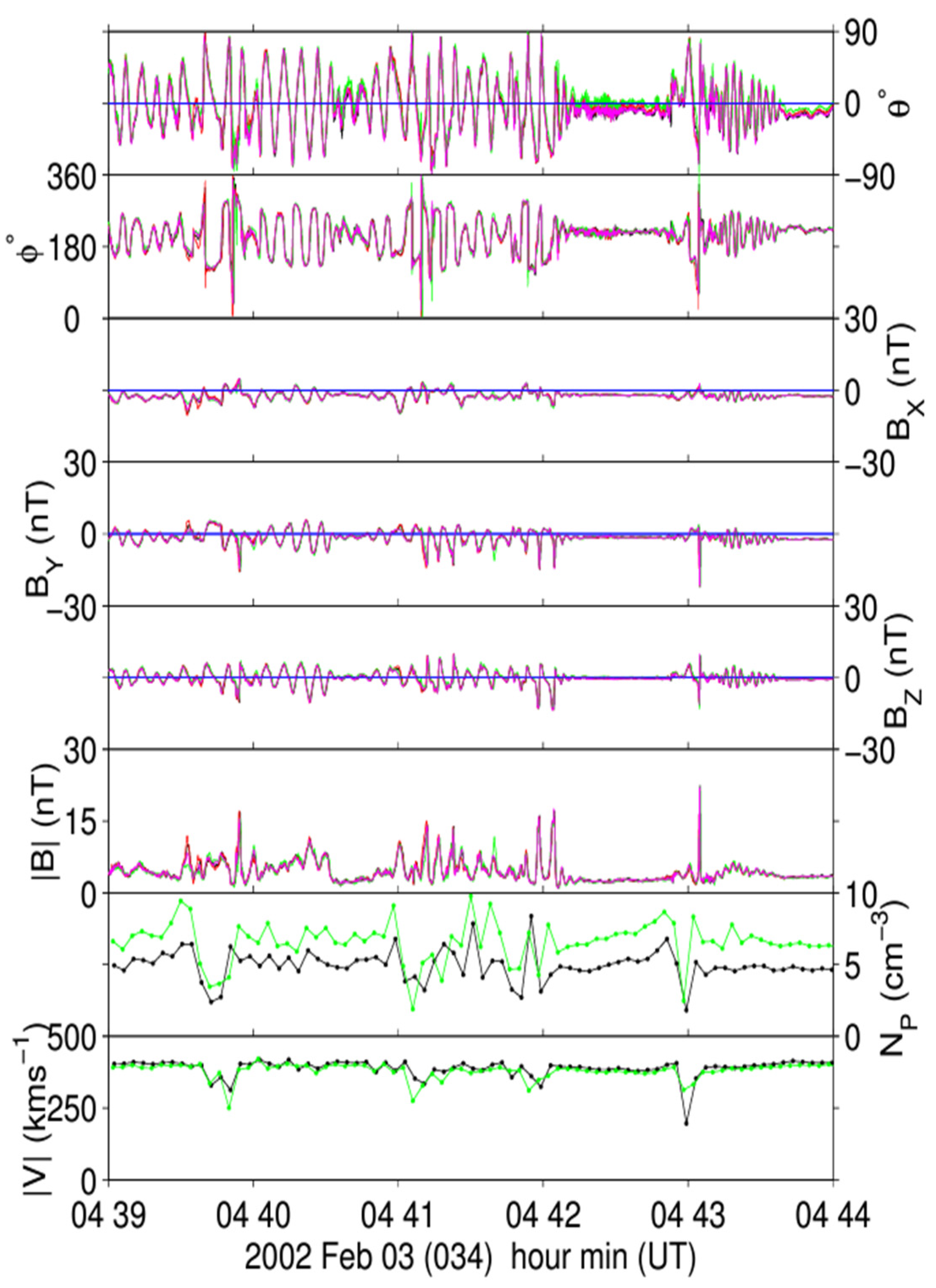
Figure 2.
CLUSTER measurement (obtained on 3 February 2002) of at interval upstream of the quasi-parallel bow shock when both ULF waves and steepened SLAMS were present(from [
101]).
Figure 2.
CLUSTER measurement (obtained on 3 February 2002) of at interval upstream of the quasi-parallel bow shock when both ULF waves and steepened SLAMS were present(from [
101]).
Originally defined as brief monolithic features in the magnetic field, with amplitudes exceeding double the background field [
102], SLAMS manifest during crossings of quasi-parallel bow shocks, which are typically greatly disturbed, showing spiky electromagnetic fields instead of clearly defined transitions. Recent observations related to SLAMS have been made during the Magnetosphere Multiscale (MMS) Mission by [
103], who suggested a connection between the scale size of magnetospheric jets and the rippling of the bow shock, which is thought to be related to SLAMS.
Bow shocks of outer planets are generally stronger than those of inner planets due to their higher Mach numbers [
104]. For planets with stronger bow shocks, the flux of backstreaming particles is higher, leading to increased rates of particle acceleration ([
105,
106]). At Earth, SLAMS have a typical duration of about 10 s [
89], while at Saturn, the duration is approximately 1–2 min, reflecting differences in upstream conditions such as lower interplanetary magnetic field strength and solar wind density.
5. Observational Evidence on the Relationship Between Upstream Waves and Ground Geomagnetic Pulsations
Ref. [
107] first pointed out an important relationship between the interplanetary magnetic field and ground pulsations, namely that the direction of the IMF affects the occurrence frequency of Pc3 waves observed on the ground. According to these results, along with those of others (e.g., [
108,
109,
110,
111,
112,
113,
114,
115]), daytime Pc3 pulsations appear on the ground when the cone angle is smaller than 50°–60°. Based the empirical data, many authors found maximum pulsation activity at a cone angle of 0° ([
109,
111,
116]), while others observed this activity at around 30° ([
117,
118,
119]).
Ref. [
120] also reported a clear relationship between the frequency of Pc2-4 geomagnetic pulsations recorded on the ground and the magnitude of the interplanetary magnetic field. Later, a series of studies ([
118,
121,
122,
123]) confirmed these results (for further references, see [
122,
124,
125]). The same relationship was also found to be valid in the foreshock region ([
59,
90]), as well as in the magnetosphere ([
116,
126]).
Later on, a series of studies ([
118,
121,
122,
123]) confirmed these findings (for further references, see [
124,
125]). Moreover, the same relationship was also found to be valid in the foreshock region ([
71,
127]), as well as in the magnetosphere ([
116,
126]). All these observations point to the upstream origin of the dayside Pc3-4 pulsations.
The dependence of the activity of various types of ULF waves on the solar wind speed is also well documented ([
128]). For example, ref. [
129] found that the correlation between the amplitude of daytime Pc3 pulsations and the solar wind speed maximises at around 40 mHz, which is close to the theory-predicted upstream wave frequency under typical interplanetary conditions.
More recently, Refs. [
113,
115] found that the dayside Pc3 activity also depends on the density of the solar wind. Under extremely low (<1 cm
−3) density, ground Pc3 waves disappear (
Figure 3). This is probably caused by the fact that the solar wind then becomes sub-Alfvénic and is thus unable to sweep the upstream propagating waves back towards the magnetosphere. At low Mach numbers, the bow shock also weakens, and the ions are reflected less efficiently ([
113]). At low solar wind speed and/or low density, the kinetic energy available to drive instabilities is also limited. All these factors play some role in controlling the ULF activity within the magnetosphere and on the ground.
These observations pointed to the upstream origin of the daytime Pc3-4 pulsations observed in the magnetosphere and on the ground.
6. Transmission Through the Magnetosheath and Propagation in the Magnetosphere
ULF waves are crucial for mass, momentum, and energy transport in the magnetosphere. Understanding their global properties and energy transport mechanisms from the solar wind to the magnetosphere, ionosphere, and ground is essential. Earth’s magnetospheric activity is primarily influenced by the solar wind plasma and the interplanetary magnetic field (IMF). Energy coupling between the solar wind and Earth’s magnetosphere often excites various plasma waves, including ULF waves. In the 1940s, ground-based magnetometer observations identified geomagnetic signals related to interplanetary shock impacts, later identified as driven by coronal mass ejections (CMEs) or corotating interaction regions (CIRs). Solar wind dynamic pressure pulses can significantly affect the magnetosphere, either compressing or inflating it, launching fast magnetosonic waves that form standing ULF waves. These waves can transport solar wind energy into the magnetosphere and sometimes, into the plasmasphere. The generation mechanisms of dayside ULF waves vary by region. The Kelvin–Helmholtz instability, requiring a shear flow to meet its instability threshold, primarily occurs on the dawn and dusk flanks of the magnetopause. In contrast, dynamic pressure pulses are responsible for ULF waves in the dayside local noon region.
The discovery of empirical relationships between the upstream waves and surface geomagnetic pulsations immediately raised the question of where and how the waves generated in the foreshock enter the magnetosphere. This question has not been answered satisfactorily to date. Despite decades of research ([
130,
131,
132]), the transmission of foreshock ULF waves across the bow shock and the turbulent magnetosheath remains unclear. Refs. [
84,
133] studied the propagation of ULF waves in the foreshock and in the magnetosheath using the wave telescope technique, making use of the multipoint observations of the Cluster mission. Although they found upstream propagating (in the solar wind frame) waves in the foreshock and earthward propagating modes in the magnetosheath (
Figure 4), the wave populations, as well as the wave modes found inside and outside the shock, proved to be unrelated. The magnetosheath was found to be dominated by the mirror and ion cyclotron modes, while fast magnetosonic waves (the wave mode of ULF waves of upstream origin, as observed in the magnetosphere) were not detected ([
84,
134]).
In a recent global kinetic ion simulation study, using the hybrid-Vlasov (Vlasiator) simulation code, ref. [
81] managed to reconstruct the passage of the upstream waves through the magnetosheath and their entry into the magnetosphere (
Figure 5). The frequency of the waves entering the model magnetosphere showed a dependence on
Bimf, which is similar to the behaviour of the foreshock waves, and in agreement with other observations, the magnetospheric intensity showed a clear dependence on the cone angle and the solar wind speed. However, the simulation produced fast magnetosonic activity in the magnetosheath, where this wave mode has never been observed, as previously mentioned.
Once compressional ULF waves enter the magnetosphere, they can propagate isotropically through the magnetosphere. In the inhomogeneous magnetosphere, compressional and shear Alfvén modes are always coupled; thus, the compressional waves launch Alfvén waves along the geomagnetic field lines they cross. The coupling is the most efficient where the frequency of the compressional driver matches the eigenfrequency of the geomagnetic field line (
ω/
k‖ =
vA). In this case, the Alfvén wave builds up a field line resonance ([
135,
136]). A broad-band driver simultaneously excites a range of field line resonances at a range of eigenfrequencies. Thus, some part of the compressional wave energy entering the magnetosphere near the subsolar point (or the flow stagnation point on the magnetopause) and propagating inward couples to the Alfven waves and reaches the ionosphere, guided along the field lines ([
137,
138,
139]). This combined propagation path (isotropic compressional plus field-guided Alfvén) is often referred to as the Tamao path ([
137,
140]).
The remaining incoming compressional energy penetrates deeper. During the propagation, the waves become weaker due not only to the loss resulting from mode coupling but also as a consequence of geometric attenuation ([
140]). Propagating inward, the waves travel through an increasingly dense medium. At some point (the turning point), waves cannot propagate further but are reflected ([
141,
142]). The rest of the magnetosphere is not transparent for the waves. Magnetosonic waves propagate only as long as the wave equation has a solution. Since both the wave propagation speed (
vA) and the azimuthal wave number
kφ are a function of the location, the cutoff frequency is also a function of location. In the WKB approximation ([
141]), the cutoff frequency
ωmin is given by the following:
where r is the radial distance, and L is the McIllwain parameter. Since kφ = 2π/λφ = m/r, with λφ and m as the azimuthal wavelength and wavenumber, respectively, and assuming a simple power-law radial plasma density distribution (r−α) in a dipole magnetic field, the equatorial Alfvén speed scales as L−3+α/2, and so, the following is obtained:
where ϱmp is the plasma mass density at the magnetopause ([141]). Substituting realistic values (m = 3, n = 3, ϱmp = 1 cm−3), fmin = ωmin/2π is 81 mHz, 46 mHz, 29 mHz, 20 mHz, 14 mHz, and 11 mHz for L = 4, 5, 6, 7, 8, and 9, respectively. This means that higher-frequency ULF waves penetrate deeper into the magnetosphere.
The waves that reach as deep as the plasmapause (where there is a step-like increase in the density and a corresponding drop in
ωmin,) can propagate further from that point toward the ionosphere. According to this model, the typical 30 s waves cannot reach beyond the L = 6 shell. This finding of [
141] has led many researchers to question the relationship between the upstream waves and the ground pulsations.
In his later more realistic model, including a plasmasphere, Lee (1996) [
143] showed that waves around 25–30 mHz do reach the plasmapause under average conditions and subsequently, at least the L = 3 shell. The magnetosphere focuses the incoming waves around the equator, i.e., the waves have the best chance to approach the ionosphere near the equator.
At the point of the total reflection, the reflected magnetosonic waves couple to the non-propagating, exponentially decaying evanescent mode ([
141,
144]). Thus, even if not directly, upstream waves may also reach the ionosphere ([
139,
145]).
7. Waves at the Ionosphere and Transmission Through the Ionosphere
ULF wave observations at low-Earth orbit (LEO) have confirmed the above scenario. Compressional ULF waves of upstream origin have been clearly identified in the recordings of the Oersted [
146], CHAMP [
139], and Swarm [
147] satellites. Reports on field line resonances driven by the upstream wave activity, as well as on their statistical investigations, have also been published ([
136,
148]). In line with the propagation model, compressional Pc3 wave power at LEO is concentrated near the equator and at around MLT = 11 (
Figure 6a) [
139]. The coherence length of compressional Pc3 waves was found to be of the order of 1000–10,000 km (
Figure 6b), and practically all of the dayside waves fluctuate in-phase ([
139,
147]).
Transmission through the ionosphere has also been studied for decades. While compressional waves are not reflected efficiently and can easily break through the ionosphere, shear Alfvén waves are typically reflected under dayside conditions. This is a necessary condition for the development of the geomagnetic field line resonances. However, upon reflection, a portion of the incoming Alfvén wave power mode is converted and is reflected in the compressional mode ([
145,
149]).
Upon transmission through the ionosphere, Alfvén waves are rotated by 90° ([
135,
150,
151]). Field-aligned, fluctuating currents carried by the Alfvén waves are closed in the ionospheric E-layer (at ~100–110 km altitude) by Pedersen currents flowing along the wave electric field. However, the magnetic field of the Pedersen current and the field-aligned current cancel each other below the ionosphere, assuming a homogeneous ionosphere and a vertical magnetic field (Fukushima). Ground signatures of Alfvén waves are thus produced exclusively by the ionospheric Hall currents (which flow perpendicular to the wave electric field). Hence, field line resonances, which typically oscillate in the azimuthal directions (east–west) in the magnetosphere, can be observed in the north component on the ground.
Compressional waves do not display associated current fluctuations and are not the subject of this rotation. According to the existing models [
145], they should exhibit the same polarisation and oscillate in-phase above and below the ionosphere.
However, compressional waves have been observed in-phase only on the nightside, while on the dayside, they are typically observed in the anti-phase. Strong coherence was found between mid-latitude ground stations when both the station and the satellite were on the dayside, and when the satellite was at equatorial, low, or mid-latitudes [
139]. The main features of the ground-LEO observations of the transmission of compressional and Alfvén waves through the ionosphere have been successfully reconstructed using an MHD model [
145].
8. ULF Waves and SLAMS in the Plasma Environment of Mercury
ULF wave activity in Mercury’s magnetosphere was first observed using magnetometer data from Mariner 10 during its 1974 flyby. Initial observations showed right-handed circularly polarised waves, with a period of around 3 s, near the dawn side magnetopause. As Mariner 10 moved deeper into the magnetosphere, these waves transformed into narrowband, linearly polarised waves, with a period of 2 s. The transition to linear polarisation suggested the possibility of a resonance, potentially a fourth harmonic of the fundamental field line resonance frequency, according to [
152,
153] later argued that this wave could not be a pure field line resonance, as seen in Earth’s magnetosphere, due to a significant compressional component. Southwood suggested that these waves might be analogous to Earth’s standing waves, modified by the presence of hot plasma. Ion reflection is a common characteristic of high Mach number collisionless shocks (e.g., [
61,
78,
154,
155]). Investigating the Hermean foreshock is important in order to understand ion reflection and related physical processes occurring under low solar wind Mach numbers (e.g., [
156,
157] Slavin and Holzer, 1981). The solar wind Alfvénic Mach number range observed at Mercury is ~4–6, which is just above the critical value, where particle reflection at the bow shock should occur ([
44]).
The first orbiter mission to Mercury, the MErcury Surface, Space ENvironment, GEochemistry, and Ranging (MESSENGER) [
158] spacecraft’s four-year orbit around the planet, provided excellent opportunities for long-term investigations of its plasma environment. MESSENGER arrived at Mercury on 18 March 2011, and entered into an approximately 12 h period, high eccentricity (periapsis ~ 200 km, apoapsis ~ 15,200 km) orbit with an inclination of 82°. The orbit was modified by 16 April 2012, with an adjusted period of ~8 h, and the apoapsis was lowered to around 4.1 Mercury radii (~4100 km from the surface). MESSENGER’s orbit was also favourable for studying the foreshock and various regions of the magnetosphere. ULF wave activity has been observed at Mercury on several occasions. Shortly after its orbit insertion, the MESSENGER spacecraft detected strongly coherent ULF waves with a frequency of 1 Hz in Mercury’s magnetosphere ([
159,
160]). The frequency fluctuated between the local He+ and proton cyclotron frequencies. During a statistical study spanning 2.5 years ([
161]), waves were detected in the frequency range of 0.4 to 5 Hz, with the transverse component dominating in 25% of the cases, exhibiting frequencies of 1–2 Hz.
8.1. Recent ULF Wave Observations at Mercury
The first comprehensive study on ULF waves in Mercury’s foreshock has been conducted by [
47], using the high-resolution magnetic field data (
Figure 7). Their findings indicate that waves peaking in power spectral density between 0.05 and 0.41 Hz exhibit near-circular polarisation, propagate quasi-parallel to the background magnetic field (approximately 10 degrees) and quasi-antiparallel to the solar wind velocity (approximately 165 degrees), with a relatively low normalised wave amplitude (δB/|B0| ~ 0.2). These characteristics resemble the “30 s waves” observed in Earth’s foreshock, attributed previously to fast magnetosonic waves generated by backstreaming protons. In contrast to Earth’s foreshock, the normalised wave amplitude and occurrence rate of these waves (~0.5%) appear lower in Mercury’s foreshock, likely due to reduced backstreaming proton fluxes under Mercury’s relatively low solar wind Alfvénic Mach number. These differences may also stem from Mercury’s smaller foreshock size and variable solar wind conditions. Additionally, their estimation suggests that the velocity of resonant backstreaming protons parallel to the magnetic field in the solar wind reference frame (normalised by the solar wind speed) ranges from 0.95 to 2.6. These results indicate particle acceleration at Mercury’s bow shock comparable to other planetary bow shocks in the solar system, despite Mercury’s low solar wind Alfvénic Mach regime.
In another study, ref. [
48] examined the favourable conditions for the generation of ULF waves in Mercury’s foreshock. They analysed the dependence of the 0.05–0.41 Hz ULF wave occurrence rate of the IMF intensity and cone angle; these parameters influence the foreshock size, the linear wave growth rate of plasma instabilities, and the Alfvén Mach number. MA affects the solar wind backstreaming proton fluxes responsible for ULF wave generation. Waves preferentially occur with a quasi-radial IMF configuration, and the ion–ion right hand resonant instability is likely responsible for these waves, as indicated by the consistent wave polarisation and frequency range, similar to the 30 s waves reported in the terrestrial foreshock. Waves also tend to occur at relatively low IMF intensity, corresponding to higher
MA, which is generally linked to increased particle reflection at the bow shock. Detection of ULF waves throughout Mercury’s orbit suggests that conditions for backstreaming ions are likely present at all of Mercury’s heliocentric distances. The most important conclusion, however, is that the wave occurrence rate increases with heliocentric distance (
Figure 8), and that this trend was observed during the entire mission. It also correlates with the abundance of backstreaming protons, which is partly due to the radial decay of the IMF intensity from the Sun. Furthermore, an additional variable affecting wave abundance is solar wind proton density. This density decreases with heliocentric distance, thus lowering the Alfvén Mach number for a relatively constant solar wind speed. However, it is important to note that solar wind proton density not only affects the Alfvén Mach number but also the linear wave growth rate and the flux of reflected solar wind protons at the Hermean bow shock.
Ref. [
49] characterised the ULF wave activity, power, polarisation, and frequency in Mercury’s magnetosphere on a global scale. Observations indicate that wave power is prevalent throughout the magnetosphere, with compressional waves contributing more significantly than azimuthal or poloidal waves to wave power. Azimuthal wave power is most commonly observed within the dayside magnetopause, suggesting that interactions with the solar wind, such as the Kelvin–Helmholtz instability, may drive ULF wave activity within the magnetosphere, possibly through field line resonance. Compressional wave power is present throughout the magnetosphere, peaking near midnight close to the planetary surface. The wave power also delineates the likely location of a polar cap boundary, consistent with the KT14 magnetic field model, where minimal wave activity occurs on the open field lines poleward of the boundary, and substantial wave activity is observed on the closed field lines towards the equator of the boundary.
The distribution of wave power (
Figure 9) in the magnetosphere shows concentrations near the dayside magnetopause and in the near magnetotail (towards dawn). The concentration of wave power (especially azimuthal) on the dayside magnetopause suggests that the interaction with the solar wind could be a major source of ULF wave activity at Mercury. Excluding the compressional waves (these are related to the high wave power in the magnetotail), the entire dayside magnetosphere and the flanks are dominated by azimuthally oscillating ULF waves. This dominance of azimuthally oscillating wave activity is highest in the vicinity of the planet, indicating that the solar wind interaction could drive toroidal field line resonances (FLR) similar to those observed in the terrestrial system.
The polarisation of these transverse waves shows a clear reversal around the noon–midnight meridian. The handedness of the waves on each side of the magnetosphere suggests that they inherit their polarisation state from anti-sunward propagating features of the solar wind, such as Kelvin–Helmholtz magnetopause waves. This feature is well-known in the Earth’s magnetosphere. In Mercury’s multicomponent plasma environment, resonant mode coupling could occur with the shear Alfvén mode when the frequency is considerably lower than the lowest ion gyrofrequency among the components. If not, localised coupling may be observed at the crossover frequency. It is possible that solar wind-related wave activity could couple with toroidal FLRs or the local crossover frequency.
The spacecraft’s rapid transition through the magnetosheath and the steady solar wind conditions during the analysed period allowed for an investigation of both the spatial and temporal properties of the shock crossings [
162]. The observations indicated that under stable solar wind conditions, the shock reformation process (
Figure 10) can be nearly periodic. In
Figure 10, the low-amplitude ULF waves are shown on the right, and the large-amplitude magnetic structures from bow shock reformation are shown on the left. Over five wave periods (15:53:10 to 15:53:50 UTC), a gradual amplitude change is observed, indicating a connection between the phenomena. A steepening is seen on the left (downstream) side of both the fully developed and intermediate structures, contrary to typical observations at the terrestrial bow shock.
During a measurement interval of 25 min, the periodicity of the magnetic field oscillations only deviated ~10% from that of the average 10 s period measured. It was also demonstrated that bow shock reformation can be a significant source of wave activity in the magnetosphere, generating oscillations in the magnetic field with amplitudes of 40–50 nT over large areas in the dayside magnetosphere. The clear and cyclic behaviour observed during this event in the upstream region, as well as throughout the magnetosphere and magnetosheath, suggests that the subsolar region was predominantly influenced by a cyclic reformation of the shock front.
8.2. Recent Simulation Results of the Hermean Foreshock
Ref. [
163] used a 3D hybrid simulation to model the ion foreshock and large-scale ULF foreshock wave activity at Mercury. In the simulation, a portion of the incident solar wind ion flux (comprising both solar wind protons and alpha particles) is scattered back upstream near the quasi-parallel bow shock regime. The upstream conditions were set to represent nominal solar wind and IMF at Mercury’s perihelion.
Their analysis reveals a dynamic Hermean ion foreshock upstream of the quasi-parallel bow shock of Mercury. Simulation of the global magnetic field configuration (variation of the B
y component) is shown on
Figure 11. The backstreaming solar wind particles represent the suprathermal foreshock ion population, of which a significant fraction exhibits sunward-pointing velocity components. This near-foreshock (at a few Mercury radii from the planet) region is associated with large-scale oblique fast magnetosonic waves in the ULF regime that propagate downstream with the solar wind. Under the specific upstream conditions analysed, in the simulation, the period of the ULF waves in Mercury’s foreshock was found to approximately 5 s, which corresponds to the 30 s foreshock waves observed at Earth, when adjusted for the magnitude of the IMF.
Ref. [
164] have investigated the role of the morphology of Mercury’s magnetic field and the foreshock region in ULF wave generation, using a 3D hybrid simulation in which ions were treated as particles, and electrons were represented as a massless charge-neutralizing fluid. This model has recently been applied to study ULF waves in the foreshocks of Mercury [
163], Venus [
165], and Mars [
166]. While modelling the first flyby of the BepiColombo mission to Mercury, they found evidence for ~2-s circularly polarized right-handed waves in the magnetosphere, with the most intense wave power observed on the dawn-side closed magnetic field lines. These waves were observed to originate from the hemisphere that is magnetically connected to the interplanetary magnetic field on the dayside and to the planetary foreshock. Thus, it is likely that the generation mechanism of these waves is related to the precipitating ion flux or the wave activity in the foreshock.
8.3. SLAMS Observations at Mercury
The possible existence of SLAMS (short large-amplitude magnetic structures) in Mercury’s foreshock has been considered by [
167] as they examined a MESSENGER spacecraft traversal through the magnetosheath and quasi-parallel foreshock region. They detected what they termed ‘large-amplitude magnetic structures’, but did not provide specific amplitude measurements. Rather than interpreting these structures as SLAMS, they viewed them as larger-scale cyclic reformations of the bow shock. They observed nearly periodic waves in stable solar wind conditions and stated that bow shock reformation could be a significant source of magnetospheric wave activity. Instead of aligned SLAMS structures (as in Earth’s quasi-parallel bow shock), at Mercury, bow shock cyclic reformation is more likely to occur. Their argument was based on the clear cyclic behaviour of these structures, with similar amplitudes for each consecutive magnetic field peak, which differed from the typically observed monolithic structures of SLAMS [
89]. They also noted that the same distinct cyclic behaviour was observed in the downstream magnetosheath and even in the magnetosphere, suggesting that the structures possessed a large cross section. A patchwork of smaller, SLAMS-like structures would not produce such stable periodicity in the downstream waves. Additionally, the polarisation of the structures matched that of the upstream ULF waves, which is not characteristic of SLAMS at Earth. Ref. [
167] also argued against the presence of SLAMS at Mercury, citing the rarity of magnetic compressive structures (‘paramagnetic plasmoids’, as per [
168]) in the magnetosheath. At Earth, such structures are interpreted as remnants of SLAMS that have crossed the bow shock, thus suggesting that the existence of SLAMS at Mercury is unlikely.
The first comprehensive study of SLAMS at Mercury was presented by [
169]. They used four years of magnetic field measurements from the MESSENGER spacecraft to investigate and identify SLAMS in the Hermean foreshock. For their analysis, they defined SLAMS as magnetic field compressional structures, with an increase in magnetic field strength of at least twice that of the background field, when MESSENGER was in the solar wind. A total of 435 SLAMS events were identified. These were found either in regions of a general ultra-low frequency (ULF) wave field, at the boundary of such a ULF wave field, or, in a few cases, isolated from the wave field (
Figure 12). The majority of the SLAMS were found within 2 R
M of the model bow shock, as measured both along the Sun–planet line and along the IMF, referred to as “transition region” by [
92]. Statistics for several properties of the SLAMS, such as temporal scale size and amplitude, were presented. It was determined that SLAMS are mostly observed during periods of low interplanetary magnetic field strength, indicating that they are more common for higher solar wind Alfvénic Mach numbers (
MA). They also established that the observed SLAMS were found on field lines connecting to the bow shock, and for a few cases right-hand elliptical polarisation was shown as well. These features are consistent with SLAMS observed in the terrestrial plasma environment. Although SLAMS are expected to be observed along field lines connected to the quasi-parallel bow shock, at Mercury, they also observed SLAMS-like structures in the quasi-perpendicular regime. It is known that—especially when the IMF is more radially oriented, characteristic of the quasi-parallel regime—the foreshock can extend into regions of
ϑBn ≈ 60° ([
170,
171], which was consistent with the observations presented by [
169].
In some cases, a whistler-like precursor wave can be observed (
Figure 13) at the upstream edge of SLAMS (similarly observed at Earth, see
Section 4, and Saturn, see
Section 9) as a common indicator that these magnetic structures locally behave as quasi-perpendicular shocks. For the whistler-like waves observed at Mercury, the frequency was roughly twice the local proton gyrofrequency, with almost circular polarisation. At Mercury, the frequency of ULF waves was only about 40% of the proton gyrofrequency during the initial measurements. The explanation for this lies in the mixture of solar wind-originating hydrogen and helium, as well as crust-derived oxygen, sodium, magnesium, and silicon in Mercury’s environment.
These results suggest that the upcoming BepiColombo mission should aim to observe both the foreshock ion populations upstream of the quasi-parallel bow shock and the ULF fluctuations in plasma density and the magnetic field, both upstream and inside of the magnetospheric boundary, to obtain a more comprehensive knowledge about the intricacies and further implications of coupling between plasma waves and magnetospheric dynamics.
9. ULF Wave and SLAMS Observations at Saturn
Of the outer planets, here we only mention Saturn, since thus far, this is the only giant planet for which a more detailed study on the properties of upstream ULF waves and their connection to SLAMS has been established and studied. Since July 2004, the Cassini spacecraft has observed Saturn’s plasma environment, traversing the foreshock region multiple times. Ref. [
58] analysed the time period from Cassini’s Saturn orbit insertion (SOI) in June 2004 to August 2005, using the measurements from a vector helium magnetometer (VHM). They identified two distinct types of ULF waves: those with frequencies below and above the local proton cyclotron frequency. These waves, associated with Saturn’s foreshock, exhibit amplitudes comparable to the mean magnetic field. Their survey revealed that the ULF wave foreshock exhibits a well-defined boundary, linked to changes in θ
Bn for the quasi-parallel geometries. Frequencies below the local proton cyclotron frequency corresponded to phase-steepened waves with periods of 5–10 min and were often accompanied by precursor whistler wave trains. These were likely ion–ion resonant right-hand (fast magnetosonic) mode waves that steepen nonlinearly and emit whistlers. Waves above the proton cyclotron frequency showed quasi-monochromatic or steepened characteristics with periods around 1 min and exhibited right-handed polarization and slightly oblique propagation relative to the IMF. Ref. [
58] mapped, for the first time, the ULF wave foreshock boundary for Saturn, identifying 21 stationary crossings, inbound and outbound. They found no clear dependence between the boundary and the IMF cone angle.
SLAM structures at Saturn have only recently been studied in more detail [
50]. Using data from the Cassini spacecraft’s Magnetometer and Plasma Spectrometer (CAPS), they investigated four SLAMS events in detail, primarily during the period between 2004–2005, when Cassini repeatedly passed through the quasi-parallel bow shock. The four events discussed were located in the dusk-noon sector SLT (Saturn Local Time) of Saturn’s upstream region. They observed multiple bow shock crossings during each event, as Saturn’s magnetosphere and bow shock pulsate dynamically in response to fluctuations in the dynamic pressure and the IMF. The upstream plasma parameters and the observed locations of the structures relative to Saturn were quite similar during the events. The plasma parameters in the undisturbed solar wind during the observations were also considered. The ion and electron temperatures were ~1 eV [
172], and for the solar wind density, they used an approximation of ~1 cm
−3. The plasma beta of Saturn is expected to be about 0.9, with the magnetosonic Mach number (
MMS) being ~9 (e.g., [
172,
173,
174]). Locally, the SLAMS act as a fast-mode shocks, and like at Earth, in the case of these magnetic structures observed at Saturn, ion beam reflection, multiple beams, deceleration, and plasma heating of the solar wind protons were detected [
50]. An example measurement series of ULF waves and steepening SLAMS upstream of the quasi-parallel bow shock of Saturn is shown in
Figure 14.
It was observed at Earth (and also mentioned in
Section 8 in regards to Mercury) that during the steepening process, the leading edge of the SLAMS emits a whistler precursor (e.g., [
173]) that departs from the structure’s edge and will behave as a new shock front [
87], with quasi-parallel characteristics. Examples of SLAMS-related whistler waves detected in Saturn’s foreshock are shown in
Figure 15. On the hodogram (top right) the arising whistler and a circularly polarised wave can be seen, as the polarization and the amplitude suddenly change. We cannot transform the measurements into the plasma frame of reference, but the changes in polarization are clearly visible.
The size of the SLAMS scales with the ion gyroradius, which depends on the magnitude of the upstream magnetic field. It also determines the frequency of the ULF waves, from which SLAMS may arise. The foreshock ULF wave frequency increases for larger B, and it also depends on the IMF cone angle (decreasing for increasing angle value) (e.g., [
90,
174]). Towards the outer heliosphere, the plasma density and the IMF strength gradually decrease, so the frequency of ULF waves would decrease as well in planetary environments farther away from the Sun, resulting in more spatially extensive magnetic structures. By comparing the observations from Saturn with the terrestrial measurements, the duration of SLAMS events was found to be considerably longer than at the foreshock of Earth. The duration of a SLAMS at Saturn is ~1–2 min, suggesting a linear size of ~30,000 to 50,000 km, since the spacecraft velocity was negligible relative to the solar wind speed. At Earth, the average SLAMS duration is ~10 s (correlation at 100 km in CLUSTER measurements). Note that although the spatial size of the magnetic structures is significantly larger than that near Earth, the energization of particles appears to be prompt, just like in the terrestrial case. The observed features of SLAMS at Saturn, however, are fundamentally consistent with the physical characteristics of cases studied near Earth.
10. Comparing Observations Between Mercury, Earth and Saturn
According to simple model calculations, the average Parker angle at Mercury, Venus, Earth, Mars, Jupiter, Saturn, Uranus, and Neptune is 23°, 38°, 45°, 57°, 80°, 84°, 87°, and 88°, respectively [
175], while the observed averages are somewhat higher: 22°–27° at Mercury; 40°–49° at Venus, 48°–53° at Earth [
176], and 56°–60° at Mars. This implies that low-frequency waves, driven by the anomalous ion cyclotron resonance, can likely be observed at these planets as well. Indeed—apart from the previously discussed cases of Earth and Mercury—ULF waves (and in Saturn’s case, SLAMS) have recently been observed for Venus (e.g., [
177,
178], Mars (e.g., [
179]), Jupiter (e.g., [
180]), Saturn (e.g., [
50,
58]), and Uranus (e.g., [
156]) too.
The frequency of the ion gíroradius, correlating with the frequency of ULF waves in the foreshock (and also with the size of SLAMS), depends on the magnitude of the interplanetary magnetic field. The frequency of ULF waves increases with increasing magnetic field strength and is also dependent on the cone angle of the interplanetary magnetic field (decreasing with increasing cone angle) (e.g., [
90,
174].
In the case of Saturn, we found that although the generating physical processes are similar to those observed at Earth, SLAMS events are significantly longer in duration. At Saturn, the strength of the interplanetary space is approximately 1/10 of that measured at Earth. The estimated spatial extent of SLAM structures observed near Earth (though this can be measured much more accurately with the four Cluster probes than with Cassini) ranges in the 100–1000 km scale. However, at Saturn, the estimated extent (assuming the observation duration and a stationary probe relative to the plasma) falls within the ~30,000–50,000 km range.
Table 1. shows the typical values of ULF wave frequency, B
IMF, and the solar wind density for the different planets.
These temporal scale sizes can be used to compare the SLAMS phenomena observed at other planets in relation to the terrestrial ‘30 s’ ULF waves. In
Figure 16, an inverse temporal scale is shown [
169] for SLAMS at Mercury, Venus, Earth, and Saturn, as a function of the typical magnetic field strengths measured at these planets. For the temporal scale sizes, we used the midpoint of the time scale intervals from studies conducted by [
89,
178], and [
50] for Venus, Earth, and Saturn, respectively. For Mercury, we used the mean value from our current investigation. The magnetic field strengths were based on the observational fits of interplanetary magnetic field strength dependence on heliocentric distance provided by [
181].
It is established [
132] that the frequency of the ‘30 s’ ULF foreshock waves at Earth in the spacecraft frame depends linearly on the interplanetary magnetic field strength (B
IMF). If this relationship holds for other planets and if SLAMS develop by steepening a half-period relative to ULF oscillations, SLAMS should exhibit the same dependence on B
IMF.
Figure 16 confirms this linear relationship.
Favourable conditions for SLAMS generation also appear to include a high Mach number. According to [
182], simulations suggest that the density of diffuse ions in the foreshock—one of the modified particle distributions described in the Introduction—is influenced by the Alfvénic Mach number. A higher density of these ions correlates with an increased likelihood of observing high-amplitude magnetic pulsations. Therefore, it is plausible that a minimum Mach number is required for SLAMS formation, assuming that other conditions are constant. Given that the Mach number at Mercury is typically lower than at Earth, this aligns with the observation that SLAMS at Mercury occur under higher Mach numbers than those usually present at this planet, making SLAMS less common at Mercury compared to at Earth, which is consistent with current observations.
11. ULF Wave and SLAMS Observations at Other Planets
Ref. [
178] presented the first observation of magnetic fluctuations consistent with short large-amplitude magnetic structures (SLAMS) in the foreshock of Venus. On 11 April 2009, the Venus Express observed three monolithic magnetic field spikes. These structures lasted between approximately 1.5 and 11 s, exhibited magnetic compression ratios between around 3 and 6, and displayed elliptical polarisation. Ref. [
183] recently published Venus Express observations from 26 February 2009, confirming the presence of SLAMS in the steady-state foreshock of Venus. The structures observed at Venus were similar to those near Earth. The two shocklets displayed magnetic compression ratios of 1.23 and 1.34, exhibiting linear polarization in the spacecraft frame. The three SLAMS showed ratios between 3.22 and 4.03, with two displaying elliptical polarization in the spacecraft frame. Statistical analysis indicates that SLAMS are associated with unusually high solar wind Alfvén Mach numbers at Venus. While their findings confirm that shocklets and SLAMS can form in the stable Venusian foreshock, they may be less common than they are at Earth. They estimate that a lower limit for their occurrence rate is less than ~14%.
ULF-waves have also been observed at Mars [
179], using the magnetic field measurements of the MAVEN spacecraft. The maximum frequency of the waves was ~0.040 Hz, which is much lower than the local proton gyrofrequency (~0.088 Hz). The ion density correlated with the phase of magnetic pulsations. The propagation direction of the waves formed an angle of 34° with the surrounding magnetic field, and the whistler mode was also detected. In the probe’s system, left-handed, elliptical polarisation was observed. However, so far, only a few foreshock ions have been detected at Mars, since both the Martian shock wave and the foreshock region are relatively small when compared to the ion gyro radius.
Large amplitude, non-linear magnetic pulsations have also been observed in the magnetosheath of Jupiter. These were strongly compressive, elliptically polarised waves that propagate almost perpendicular to the direction of the surrounding magnetic field. Their properties partly match those of magnetic pulsations observed at the Giacobini–Zinner comet [
184] and partly those observed in Earth’s plasma environment. At Earth, the waves propagated along magnetic field lines, while at the comet, the propagation direction was significantly different. Nevertheless, the source of the observed phenomenon may be derived from the same process.
Ref. [
180] observed periodic variations in the Jovian magnetosheath in the range of 10 s to several days (or even longer). These oscillations were significantly influenced by the solar wind, planetary rotation, and Io’s volcanic activity. Ultra-low frequency (ULF) waves, with periods of tens of minutes, are crucial for driving Jovian energy circulation through field line resonance. Longer periodicities are likely linked to global mass circulation. This study focuses on variations in ULF wave energy over several hours, which are challenging to identify within the magnetosphere due to the rapid modulation incurred by planetary rotation. Using magnetic field observations from Juno and Galileo in Jupiter’s magnetosheath, multiple significant multi-hour periodicities were found, ranging from 2 to 10 h and peaking at different values in each case. The most common periodicities, between 3 and 5 h, were observed on both the dawn and dusk sides, likely associated with energy transport from the inner magnetosphere to the magnetosheath.
12. Conclusions and Perspectives
This review presents a comprehensive examination of ultra-low frequency (ULF) wave observations across different planetary environments, focusing primarily at Earth, Mercury, and Saturn. ULF waves, which play a crucial role in space plasma dynamics, are investigated through data from various spacecraft missions, including Earth’s CHAMP, Swarm, and Oersted satellites; Mercury’s MESSENGER; and Saturn’s Cassini spacecraft. It can be concluded that the formation mechanism of foreshock ULF waves is very similar across the Solar System, and the basic observational features of these waves and the relating SLAMS phenomena show the same behaviour as the features observed at Earth. However, since the frequency of ULF waves scale with BIMF, due to the different heliospheric distances, we find differing spatial and temporal parameters relating to these waves and magnetic structures at the different planetary environments. Recently obtained results regarding Mercury and Saturn have made these comparative studies possible.
Furthermore, we also examined ULF wave modes, and power distributions, and possible mechanisms at the different planets. Observations from low-Earth orbit (LEO) reveal that compressional ULF waves, particularly Pc3 waves, exhibit significant power near the equator and peak around Magnetic Local Time (MLT) = 11. These waves, observed both in-phase and anti-phase using ground-based measurements, highlight a complex interaction between compressional and shear Alfvén waves as they propagate through the ionosphere. Alfvén waves are notably reflected under dayside conditions, influencing geomagnetic field line resonances, whereas compressional waves show less variation in phase across the ionosphere. ULF wave activity at Mercury has been characterized by observations from the Mariner 10 and MESSENGER missions. Initial data indicated a transition from circular to linear polarization in the ULF waves, suggesting resonant interactions influenced by compressional components. Recent findings from MESSENGER indicate a lower occurrence rate of ULF waves in Mercury’s foreshock compared to Earth’s, attributed to reduced backstreaming proton fluxes and lower solar wind Alfvénic Mach numbers. Variability in wave occurrence is correlated with heliocentric distance and solar wind density, with a notable increase in wave activity with increasing distance from the Sun. SLAMS (short large-amplitude magnetic structures) have been identified, but their characteristics differ from those observed at Earth. The study of ULF waves and SLAMS at Saturn, using data from the Cassini spacecraft, has provided insights into the dynamics of the planet’s magnetosphere. Observations reveal that SLAMS at Saturn are similar in behaviour to those at Earth but differ significantly in scale and duration. SLAMS at Saturn exhibit longer durations (~1–2 min) and larger spatial extents (~30,000 to 50,000 km) compared to those at Earth. The study also highlights the presence of whistler-like precursor waves associated with SLAMS and notes the influence of upstream solar wind conditions on the properties of these structures.
This review aims to examine the variability in ULF wave and SLAMS characteristics across planetary environments. While Earth’s observations provide a well-established framework for understanding ionospheric effects and wave propagation, Mercury and Saturn offer unique insights into the behaviour of ULF waves in environments with different solar wind interactions and magnetospheric conditions. These findings contribute to a broader understanding of space plasma dynamics and highlight the need for further investigation, particularly in the context of planetary magnetospheres. The physical conditions that determine the characteristics of the ULF waves in the foreshock and their transition into the magnetosphere show great diversity as well, and in recent years, several interesting new interactions have been observed that further enrich this intricate and multi-faceted coupling mechanism. While the Cassini mission to Saturn ended in 2017, the data analysis is still ongoing. However, the BepiColombo mission is planned to enter into orbit around Mercury in December 2025, continuing to collect observations, providing an excellent new opportunity to persist in observing its magnetosphere and its interactions with a highly dynamic planetary environment.