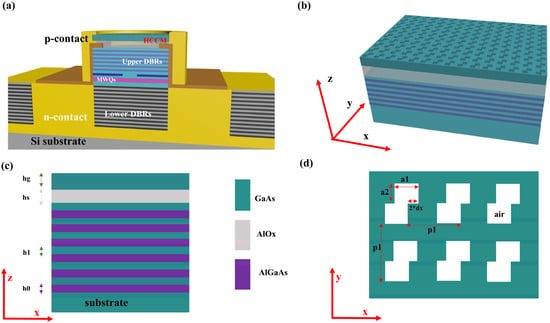
2.1. Structure and Optimization
The VCSEL is required to have a pair of highly reflective mirrors so that the gain in the resonant cavity exceeds the loss caused by the short gain medium in the direction of material epitaxy. In order to achieve excitation of the VCSEL, one of the two VCSEL mirrors is required to be fully reflective, and the other laser mirror is required to have a reflectivity greater than 99.5%. According to the basic principle of the optical cavity in laser physics, the reflectivity of the cavity deeply affects the threshold gain
of the polarized VCSEL that can be a direct response to the ease of laser excitation, and it is calculated as
where Γ is the confinement factor, is the internal loss, is the effective cavity length, and are the power reflectivities of the top and bottom reflected mirrors of the VCSEL, respectively. Equation (1) shows that mirrors are required at the bottom and top of the device, and the high reflectivity of the mirrors plays a huge role in reducing the threshold current density. Therefore, when only the left circular polarization light (LCP) is desired to be excited by the VCSEL and the right circular polarization light (RCP) is not, it is only necessary that the mirror has chirality corresponding to the difference between the reflectivity of LCP and RCP and the reflection efficiency is greater than 99.5%, and vice versa. The dichroism (e.g., circular or even linear) is a typical feature of absorption associated with polarization. However, when a polarization-dependent grating is involved, the situation becomes more complicated. This is because even without absorption, transmission or reflection can vary with polarization. For a long time, apparent dichroism [35,36,37,38], which only looks at the polarization dependence of transmission, has been studied with more fervor than the reflection circular dichroism [39]. In this manuscript, since the main element of our study is the laser, we tend to focus more on reflection than transmission. In order to more accurately characterize chiral metasurfaces, we are apprehensive to stipulate the true circular dichroism. It is the difference between the reflectivity of LCP and RCP, considering grating effects.
It is shown in
Figure 1a that the HCCM can replace the traditional upper DBR, acting as a highly reflective mirror.
Figure 1b shows the three-dimensional structure of the HCCM, and the light illuminates from the GaAs substrate below to the chiral metasurface above.
Figure 1c shows the front view of the HCCM, which consists of the chiral reflective metasurface and the upper DBRs. The chiral reflective metasurface is composed of the AlOx substrate and the GaAs layer with two air holes displaced in opposite directions.
Figure 1d illustrates the top view of the chiral metasurface in HCCM, which shows the geometric parameters of the air hole. The refractive index of the GaAs, AlGaAs, and AlOx are 3.53, 3.08, and 1.63 at 980 nm operation wavelength, respectively. The commercial software COMSOL multiphysics is employed to analyze the optical properties of the metasurface. We apply the perfectly matched layer (PML) that artificially truncates the electromagnetic far field as the boundary condition in the z-axis direction. In addition, the periodic boundary condition accompanying periodic gratings is used along the surrounding boundaries. The S-parameters of the mode in the waveguide port are extracted to obtain the corresponding amplitude and phase information of the electromagnetic far-field. The transmitted (reflected) light intensities T(R) are obtained by integrating the Poynting vector over the transmission (reflection) port.
2.2. Optical Mode and Chiral Analysis
Displacing two identical square air holes in opposite directions can effectively break the geometrical symmetry of the unit cell of the optical metasurface. The spatial symmetry mode of the unit cell changes from the common C2 symmetry (dx = 0 nm) to the chiral symmetry (dx = 80 nm). The CD of the chiral reflective metasurface i
. Here,
and
are the reflections of the metasurface in the case of RCP and LCP incidence, respectively.
Figure 2a shows the reflectance CD spectrum of the chiral reflective metasurface with two air holes. The inset in
Figure 2a illustrates the geometric evolution of the chiral unit cell from the nonchiral case with dx = 0 nm, where the mirror structure of the unit cell rotated by 180° can be reunited with the unit cell, to the chiral case, to the nonchiral case with dx = 150 nm where the mirror structure of the unit cell rotated by 90° can be reunited with the unit cell. Obviously, in the cases of dx = 0 nm and 150 nm, the CD spectrum is zero because the unit-cell structure does not possess chiral symmetry. Meanwhile, dx = 40 nm corresponds to the large bandwidth case, and dx = 80 nm corresponds to the large CD case.
Figure 2b shows the effect of the displacement (dx) of air holes on the CD. As the dx increases, the CD first increases and then decreases. The largest CD, corresponding to dx = 80 nm, is close to 0.3.
Figure 2c shows the reflectance spectrum in the case of dx = 40 nm and 80 nm, respectively. The large CD of metasurfaces can usually be verified by near-field distribution maps as well.
Figure 2d–f show the distribution of electric near-field intensity of the XZ cross-section at different peaks, and the black dashed line in
Figure 2d is the boundary of GaAs. As shown in
Figure 2d, the optical energy is mainly radiated from the GaAs dielectric waveguide (consisting of an air hole, GaAs dielectric, and another air hole) to the air transmission domain above in the case of the peak a. And the electromagnetic energy in the air domain in the RCP case is greater than that in the LCP case. In addition, the metasurface can be approximated as different light-field radiation sources resting on endpoints 1 and 2 in the case of the RCP and LCP incidence, as depicted in
Figure 2e,f.
Figure 2g–i show the distribution of electric field intensity of the YZ cross-section at different peaks; the red dashed line in
Figure 2g is the boundary of the air hole. The light energy mainly enters the air above from the narrow GaAs medium channel in LCP mode, while the light energy enters the transmissive domain from the wide air channel in RCP mode. It is obvious that RCP penetrates more easily through the chiral metasurface into the air domain.
For qualified chiral mirrors, in addition to focusing on CD value, the reflectivity should also be close to 100%. The high reflectivity of the chiral reflective metasurface is due to the destructive interference of transmitted light at the incident interface and the high refractive index contrast between the GaAs dielectric waveguide and the surrounding material.
Figure 3a shows the reflectance spectrum of the chiral metasurface in the different refractive index deviations
at the LCP incidence. The
is
, the
is the refractive index parameter of the high refractive index grating, specifically referred to here as 3.53 for GaAs, and
is the low optical refractive index of the surrounding material (value as 1.63, 1.97, 2.47, 2.97 and 3.53). It is quite obvious that the reflection spectrum shifts significantly upward with increasing
, and there are two peaks (0.89, 0.93) and two valleys in the reflection spectrum in the system of the GaAs grating with AlOx substrate. Moreover, the purple dotted line in
Figure 3a corresponds to the reflection spectrum of a ternary thin-film structure consisting of air, a 220 nm-thick GaAs film, and an AlOx substrate, which excludes the additional effects caused by the air-hole array. It is clear that only 60% of the reflectance is caused by film interface effects, and the remaining 30% of the efficiency gain is mainly due to the resonance effects of peaks 1 and 2 in the chiral metasurface. In addition, the multipole expansion method [
40] is an effective means of analyzing metasurfaces by equating microdevices to a series of sources of electromagnetic radiation, and the total scattering power is
where, P, M, Qαβ, Mαβ mean the scattering intensity of equivalent point sources from the electric dipole (ED), magnetic dipole (MD), electric quadrupole (EQ) and magnetic quadrupole (MQ), respectively. The j is the current density in the microdevice, and c represents the light speed in free space. α and β are mutually orthogonal spatial projection directions. Figure 3b shows the multipole expansion distribution of the GaAs chiral metasurface in the case of LCP incidence, and the metasurface is manipulated by MD and EQ at valleys 3 and 4, respectively. Figure 3c,d shows the distribution of electric field intensity of different peaks. Moreover, the standing waves appear in the transverse waveguide consisting of the low refractive index air hole, the high optical refractive index GaAs medium, and another low refractive index air hole. At peaks 1 and 2, the localized energy of the light field is parked in the waveguide in the Y and X directions, respectively.
It is very unfortunate that the maximum reflectivity of the chiral reflective metasurface remains some distance from the 99.5% reflectivity threshold of the VCSEL mirrors. Therefore, we had to build a few DBR pairs to increase the theoretical upper reflectivity limit by tolerating some process harshness when designing the device structure. The conventional DBR mirrors for VCSELs are composed of optical materials with high and low refractive indices stacked sequentially at a specific thickness.
Figure 4a shows the effect of the number of pairs of DBR on the reflectance. The DBR is made up of the GaAs with the high refractive index and the AlGaAs with the low refractive index. It can be shown that the reflectance increases gradually with the increase in the number of pairs of DBR. When the number of pairs of DBR is 6 and 15, the reflectance is 55% and 92%, respectively. And when the number of pairs of DBR is 20, the reflectance has converged to 100%. In addition, if destructive interference between the two mirrors can be ruled out, the combination HCCM of two mirrors (the chiral metasurface and 6 pairs of DBRs) is expected to satisfy both large CD and reflection efficiencies.
Figure 4b shows the effect of the thickness (hs) of the support layer of AlOx on the HCCM. The largest CD occurs at hs = 270 nm, while the large CD and reflection efficiency are simultaneously satisfied at hs = 150 nm.
Figure 4c shows the distribution of electric field intensity of different cross-sections at hs = 270 nm in the case of LCP incidence. For the XZ cross-section case, the electric field localization effect, which evaluates the energy leaking into the air domain, occurs at the 1 and 2 endpoints of the metasurface, and the standing waves, confined in the transverse dimension caused by the strong interference effects, appears in the AlOx support layer between the DBR and the grating. For the YZ cross-section case, the standing wave effect occurs only in the Z direction, probably due to the weak electric field localization effect at end-point 3. Moreover,
Figure 4d shows the distribution of electric field intensity of different cross-sections at hs = 150 nm. Due to optical interference, the standing waves do not exist in the AlOx layer, and the electric field localization effect corresponding to the transmissive leakage mode is also weak.