1. Introduction
Over the past few decades, the use of steel–concrete composite structures has increased significantly due to their exceptional structural performance in high-rise buildings and long-span bridges. This structural configurationintegrates the behavior of concrete and structural steel within a unified composite section to yield higher strength and stiffness when compared to traditional reinforced concrete or structural steel structures [
1,
2]. This enhanced stiffness and strength enables the design of elements with smaller cross sections, thereby improving the dynamicresponse of these structures when subjected to loads such as those generated duringearthquakes. Moreover, the use of smaller section elements results in material savings and a reduction in construction times, thereby generating economic benefits [
3].
Composite construction usually consists of a concrete slab pre-cast onto a profiled cold-formed steel sheet, and attached to a structural steel beam with a mechanical connection welded to the top flange of the steel element [
4]. The resulting composite structure possesses greater mechanical performance compared with its individual components. The primary design consideration for these composite elements is flexural bending [
5], where the concrete slab takes the stresses in compression, while the tensile stress is resisted by the steel section [
6]. For composite concrete and steel systems to behave as a single flexural element, the concrete slab and steel must be rigidly attached. Traditionally, headed steel shear stud anchors are welded to and distributed along the top of the steel element to ensure the horizontal shear is effectively transferred across the concrete steel interface [
7,
8]. However, relative longitudinal displacements occur due to the flexible shear connection, causing the concrete near the connection to crack [
9,
10].
Damage in steel–concrete composite beams is frequently relatedto long-term cyclic loads from traffic on parking buildings or bridges, fatigue on shear stud anchors, or seismic loads [
11,
12]. When damage occurs in composite structures, cracking in the concrete slab and shear connector failure-induced slip between the beam and slab are among the most common types of damage that occur during service [
13]. These damage types are the primary cause of stiffness degradation, leading to a decrease in the load-bearing capacity of the structure [
14]. Moreover, with the increasing number of existing structures entering the aging period of their life, damage of the composite structure is becoming an evident problem that appears to be crucial to study in depth.
To minimize the risk of strength reduction in composite systems, Structural Health Monitoring (SHM) can be used to assess the damage status through in situ measurements and structural analysis, preventing premature collapse [
15,
16,
17,
18]. More recently, further progress has been made toward the concept of data processing for modal identification [
19]. For instance, Mostafaei et al. [
20] presented a fully automated modal identification algorithm to identify modal parameters for an unknown system based on its output information. The proposed algorithm identified modal parameters using only one dataset of a five-story steel building structure, increasing accuracy and robustness with the repeatable result as compared to similar algorithms. Out of the various measurement techniques used in SHM,vibration-based damage detection (VBDD) methods are among the mostpowerful tools for detecting and assessing structural damage. Since damage affects the dynamic properties of structures, VBDD methods rely on changes in vibratory characteristics such as natural frequency, vibration modes, modal damping, and frequency response functions [
21]. Damage-related changes in these vibration properties include a reduction in natural frequency, an increase in modal damping, and variation in vibration modes [
22]. Among the VBDD methods, the one based on changes in vibration modes is most suitable for detecting damage because it is less affected by operational uncertainties [
23].
To detect and assess damage, the vibration modes of the initial state of the structure are compared with the current (damaged) states using a damage detection algorithm. For instance, Xiao et al. [
24] investigated the damage identification problem of a large-scale three-dimensional (3D) truss structure using a stiffness separation method to identify the damage to a truss structure. Xiao et al. [
25] extended the previous problem by applying a partial model-based damage identification method for the damage identification of long-span steel truss bridges. Xiao et al. [
26] uses the stiffness separation method to asses damage in large-scale structures. Yu et al. [
27] introduced a hybrid framework for structural damage diagnosis that combines principal component analysis (PCA), deep stacked autoencoders (DSAE), and data fusion techniques. To enhance the performance of the diagnostic model, the authors utilized the enhanced whale optimization algorithm (EWOA) to optimize the DSAE’s meta-parameters, including the dropout rate, weight decay coefficient, learning rate, and the number of neurons in the hidden layers. Seguel and Meruane [
28] used Mode Shape Curvature (MSC), Uniform Load Surface, and Strain Energy Method detection algorithms to assess the damage of an aluminum honeycomb sandwich panel. The MSC algorithm detects and locates damage using curvature vibration modes, where abrupt changes or discontinuities in curvature are caused by local loss of stiffness, representing structural damage [
22]. Curvature-based damage detection methods have been used to diagnose damage in steel–concrete composite beams. Meruane et al. [
29] presented a damage detection problem in a steel–concrete composite structure using an impact-hammer-based modal testing procedure. The mode shape curvatures change due to the loss of stiffness in the presence of cracks; a change in curvature was adopted as a criterion to quantify stiffness reduction.
During the process of identifying and assessing damage in structures, finite element (FE) models are often used to extract the vibration response of the undamaged condition. The initial response is then compared with experimental vibration measurements. However, several researchers have reported modified procedures to implement FE models to better represent the damaged condition in the vibrational response. Pachón et al. [
30] performed a numerical study based on Operational Modal Analysis at the San Jerónimo de Buenavista Monastery (Seville, Spain). This study implemented an FE model of the structure to calculate the initial and current modal responses. To represent the current condition, the model was updated using a genetic algorithm based on the ambient vibration tests. The modal responses were obtained from the updated FE model and validated with the experimental vibration modes through the Modal Assurance Criterion. Altunışık et al. [
31] performed ambient vibration tests and FE models of cantilever beams to obtain the vibrational responses in the initial and damaged state. To represent the damage state in the numerical models, an automated model updated with the use of the modal assurance criterion (MAC) and the coordinated modal assurance criterion (COMAC) in ambient vibration tests was implemented to identify the size and location of crack. However, the model updating process was used to maintain the exact boundary condition for the laboratory model. On the other hand, Sridhar and Prasad [
32] and Salazar [
33] represented the damage through discontinuities in the geometry of the model to compute the damaged vibration modes. FE models can mathematically represent composite steel–concrete beams, which are composed of nodes, elements, constitutive models, and boundary conditions. To model FE composite steel–concrete beams, several authors used many FE-technology and materials models to represent concrete and steel components. Queiroz et al. [
2] conducted FE modeling of a composite beam subjected to bending to analyze the influence of shear connector failure on the beam response in Ansys V7.0 software. The beam was modeled using Shell43, Solid65, and Combin39 elements for the steel beam, concrete slab, and shear connectors, respectively. A multilinear isotropic hardening model with the von Mises yield criterion was used to represent the concrete and steel material behavior. Hu et al. [
34] conducted an FE modeling of a composite beam to evaluate the maximum flexural capacity in Ansys Mechanical. The composite beam was modeled using the Solid65 element for the concrete slab and the Solid45 element for the steel girder and shear connectors. To represent the concrete and steel, were used the constitutive relationships proposed by Wang et al. [
35] and Esmaeily and Xiao [
36], respectively. Also, the concrete compressive and tension behavior can be modeled according to Subramani et al. [
37] and Dahmani et al. [
38] using the Solid65 element and a non-linear constitutive model with the failure criterion proposed by Willam and Warnke [
39] to model the concrete in a reinforced concrete beam in Ansys V8.0 software. Mahmoud [
40] also used a multilinear isotropic material, using the Von Mises yield criterion for steel and the Willam and Warnke failure criteria for concrete.
The objective of this study is to propose and implement an efficient vibration-based damage detection method applied to a steel–concrete composite beam finite element (FE) model, addressing critical gaps in existing research. A key innovation of this work lies in the ability of the numerical model to dynamically represent the damaged state of the structure by updating the tangent stiffness matrix through a quasi-static nonlinear analysis. This approach accounts for geometric, material, and contact nonlinearities, which are often overlooked in conventional vibration-based damage detection studies. The implementation of the Newton–Raphson method within the Linear Perturbation Modal Analysis (LPMA) framework enables the representation of stiffness degradation caused by mechanical loads. This allows for the extraction of vibration modes that incorporate the effects of structural stiffness degradation, revealing essential damage indicators such as reductions in natural frequencies and increases in vibration mode amplitudes compared to the undamaged state. Furthermore, the modal responses are analyzed using the Modal Shape Curvature (MSC) algorithm, which successfully localizes and quantifies damage in the numerical model. These results are validated by comparing with experimental bending test data from Meruane et al. [
29], demonstrating the robustness and accuracy of the proposed methodology.
3. Numerical Model
The present study employed a numerical model, which was executed using the software Ansys Mechanical 2022 R2 version. This model simulated an experimental specimen in laboratory conditions. Initial stages of numerical simulation focused on defining the geometry of the model, specifying the properties of the constituent materials, and setting the boundary constraints. The selection of finite element technology and material models available in the aforementioned software determined the mathematical model used. Geometric and material nonlinearities were addressed to account for any nonlinear response of the experimental composite beam that may arise during the simulation. These considerations are crucial for understanding the impact of stress and strain states, including nonlinear sources, on modal responses. Neglecting geometric and material nonlinearities would result in unchanged modal responses regardless of the loading state, thereby compromising the damage detection process. Without variations in modal responses, the algorithm would fail to identify damage.
3.1. Model Geometry
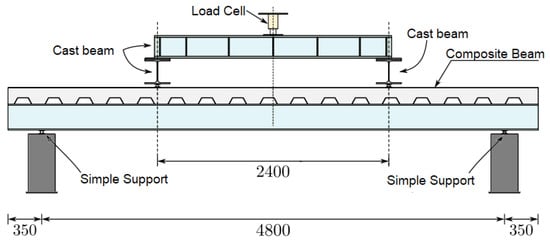
The numerical model was based on a full-scale composite concrete–steel beam that was previously investigated by Meruane et al. [
29] and constructed in compliance with Eurocode 4 [
44]. The experimental setup is depicted in
Figure 1.
The concrete slab had dimensions of 5500 mm length, 1300 mm width, and 170 mm thickness and was cast on a 0.8 mm thick steel deck profile. The slab was joined to the steel beam using 18 shear stud anchors with a diameter of 19 mm in a row along the longitudinal axis. The steel beam utilized in the experimental setup was 5500 mm long, 270 mm high, and featured flanges with a width of 280 mm and thickness of 13 mm, as well as a web thickness of 8 mm.
The model geometry was represented by 95,871 nodes and 101,534 elements, which were adapted to the dimensions and configuration of the beam components displayed in
Figure 2. To represent the structural behavior accurately, the FE model considered two planes of symmetry and simplified the geometry of the original structure. Suitable boundary conditions were defined in the model for this purpose.
3.2. Material Properties
The material properties used in the FE model were obtained from experimental data for the full-scale composite concrete–steel beam investigated by Meruane et al. [
29]. The structural response of the model was intended to match the experimental test. Two tables summarize the mechanical characteristics of the concrete and structural steel components in composite beams. These properties include the elastic modulus (
E), Poisson’s ratio (
), yield stress (
), yield strain (
), and tangent modulus (
). Additional parameters were required to define the Menetrey–Willam model for concrete as plastic strain at uniaxial compressive strength (
), plastic strain at the transition from power law to exponential softening (
), relative stress at the start of nonlinear hardening (
), residual relative stress at
(
), residual compressive relative stress (
), mode I area-specific fracture energy (
), and residual tensile relative stress (
). These parameters were defined from relations between uniaxial compressive strength and elastic modulus.
Table 1 outlines the elastic properties of G-25 concrete according experimental data by Meruane et al. [
29].
Table 2 shows the Menetrey–Willam input parameters based on G-25 concrete properties and
Table 3 reports the mechanical properties of the HEA280 section beam of grade A-36, grade 37 trapezoidal profiled sheet, and grade A-108 shear anchors according to their technical specifications. In particular, the lower Poisson’s ratio for the profiled steel sheeting is a result of manufacturing processes (such as profiling or corrugation), variations in material composition, or internal microstructure, which may influence its lateral strain response. This value differs from typical structural steel (i.e., the steel beam and stud anchors), where the isotropic response is expected when undergoing elastic deformation uniformly in all directions under stress. Numerically, a higher Poisson’s ratio of the standard steel beam may contribute to greater lateral stiffness, which might influence dynamic characteristics differently than the profiled steel sheeting with its lower Poisson ratio.
3.3. Finite Element Technology, Meshing, and Constitutive Laws
The FE technology used in the concrete slab modeling was Solid185, which represents solid structures with plasticity, stress stiffening, large deflection, and large strain, and supports linear perturbation analysis.
Figure 3 displays the finite element mesh of the concrete slab composed of 81,628 nodes and 71,352 elements. The structural steel beam and steel deck were modeled using the Shell181 FE technology, which is suitable for linear, large rotation, or large strain nonlinear applications and supports linear perturbation analysis. In
Figure 4 the structural steel beam FE mesh composed by 5362 nodes and 5166 elements are illustrated, as well as the steel deck FE mesh by 6496 nodes and 6255 elements. The shear stud anchors were modeled by the Solid185 FE technology, and their meshing involved 2385 nodes and 1368 elements. The constitutive law used to represent the nonlinear behavior of the modeled steel components was the bilinear isotropic hardening material model and the von Mises yield criterion. The constitutive stress-strain relationship is linear-elastic until the yield stress; beyond their elastic limit, the material becomes plastic due to the strains being unrecovered.
The Menetrey–Willam concrete model was utilized to simulate the mechanical response of concrete in the FE model. This model is generally better for simulating the behavior of bonded aggregates such as concrete and it is capable of capturing the material responses to both compression and tension through the Willam–Warnke yield surface, which is a stress boundary that separates the elastic and plastic regions of the stress-strain curve [
39]. This yield surface and flow potentials can be defined by the strength parameters of the concrete, such as the uniaxial yield stress, uniaxial compression, and biaxial compression. Hardening and softening functions can also be defined from these mentioned parameters to represent the hardening-softening behavior of the yield surfaces [
39].
Figure 5 shows the compressive and tension stress-strain curve of the Menetrey–Willam concrete model for a unitary specimen numerical model utilizing the material properties mentioned in
Section 3.2.
The Menetrey–Willam material model was chosen over other concrete models available in the Ansys 2022 R2 software, such as the Drucker–Prager Concrete Model, the Willam and Warnke model, and the Microplane model, based on a combination of parameter availability and compatibility with the finite element (FE) technology required to perform the Linear Perturbation Modal Analysis (LPMA) procedure. In fact, the Menetrey–Willam Model was selected because its input parameters—tensile and compressive strengths, residual stress parameters, and fracture energy—could be directly derived from accessible experimental strength data. Additionally, the finite element technology supported by this model allowed for the required LPMA procedure, enabling the simulation of stiffness degradation and modal response due to damage. On the other hand, the Drucker–Prager Concrete and Willam–Warnke models are limited by their associated finite element formulations. Specifically, the Willam–Warnke model requires the use of the Solid65 element, which is not compatible with the LPMA framework. Similarly, the Drucker–Prager model does not offer the necessary compatibility to simulate the damage effects through modal analyses. Finally, the Microplane model requires parameters, such as specific microstructural properties, that were not available within our experimental dataset. Furthermore, this model operates with the CPT215 element, which is incompatible with the LPMA procedure used in this study.
3.4. Contact Conditions
In the FE modeling of the composite concrete–steel beam, contact conditions were defined to simulate the interaction between the different components of the composite system. The FE contact technology employed for simulating these interactions is listed in
Table 4. The composite beam elements were in contact on their boundary surfaces represented by surface–surface contacts, except for the profiled steel sheet and shear anchors interaction. The edge of the profiled steel sheet was in contact with the surface of the shear anchor represented by line–surface contact. The surface–surface contact is capable of modeling the contact between 3D solid and/or shell surfaces by the contact pair Conta174-Targe170 and line–surface contact can be used to model a 3D beam or shell edge contacting solid or shell elements surfaces through the pair Conta177-Targe170. The contact behavior was defined by the standard contact model avoiding the rigid element from penetrating the flexible element, which also allows for the separation in a normal direction and the tangential sliding between the bodies in contact. In modeling the components of the composite beam, the surfaces of the components in contact were considered frictionless.In particular, the shear stud connection was modeled using a fully bonded contact behavior to simulate the weld between the shear stud and the beam, avoiding slippage and separation between the contact surfaces. Additionally, the interaction of the shear studs with other components was represented using standard contact, where normal pressure becomes zero if separation occurs, allowing gaps to form between bodies based on the applied loading.
3.5. Boundary Conditions
Boundary conditions refer to displacement constraints and external loads applied to the bodies external surfaces. The followings boundary conditions were defined to represent the loading and support conditions of the experimental four-point bending test performed by Meruane et al. [
29]. Since the FE model consisted in a quarter part of the experimental specimen, were considered additional degrees of freedom (DOFs) constraints to establish symmetry conditions.
The loading conditions for the experimental setup included two line loads applied on the slab’s upper surface. Due to the FE model symmetry conditions, the half of a line load was modeled by equivalent nodal loads in a row on the concrete upper surface displayed in
Figure 6. Meanwhile, the support conditions were established by restricted translational DOFs of the steel beam lower flange to represent the simple support condition plotted in
Figure 6, corresponding to one support of the two experimental specimen supports due to the symmetry conditions previously mentioned. Finally, the FE model symmetry conditions were modeled by constraining all DOFs
,
and
for the Y-Z plane, and
,
, and
at the nodes located in the X-Y plane reflect realistic structural behavior.
3.6. Loading Steps
The experimental test performed by Meruane et al. [
29] of the concrete–steel composite beam was subjected to a defined loading protocol presented in
Figure 7 to evaluate the damage obtained at each loading step until collapse. In order to minimize the effect on the results, the experimental loading protocol was implemented in the numerical simulation to closely replicate the results observed in the experimental tests. In this work, the finite element model presented in the previous subsection simulated the aforementioned experimental test by performing a quasi-static structural analysis by applying the experimental loading protocol to compute the stress-strain state at each loading step. Once the structural response was calculated, the methods presented in
Section 2 were applied to extract the vibration modes affected by the stresses and then detect the damage through the curvatures of the vibration modes.
5. Conclusions
In this study, an efficient approach to predicting damage using vibration-based detection techniques was presented, employing a numerical model capable of representing the structure-damaged condition by updating the tangent stiffness matrix after a quasi-static nonlinear solution. The Newton–Rhapson method through the Linear Perturbation Modal Analysis (LPMA) framework updated the tangent stiffness matrix, representing the structural stiffness degradation caused by mechanical loads including the effects of geometrical, material, and contact nonlinearities during the quasi-static solution. This allowed the obtaining of the vibration modes considering the stiffness degradation effects, playing a key role in revealing crucial damage indicators.Specifically, the reduction in natural frequencies and the increase in amplitudes of the vibration modes with respect to those calculated for the initial stiffness matrix. Then, the modal responses were used to determine the curvatures of the vibration modes performing the MSC algorithm, obtaining pronounced curvatures that confirm the presence of damage within our model and coincide with the damage observed in the experimental bending test performed by Meruane et al. [
29].
Despite that our study has demonstrated the successful application of vibration-based methods for damage detection in a numerical model capable of representing the damage condition after a static analysis, it is essential to recognize the inherent challenges associated with characterizing the specific type of damage detected, particularly in models featuring intricate or composite geometries, as exemplified in our research. The complexity of such structures introduces a level of difficulty when interpreting the type of damage due to factors such as the number of elements that compose them. In this case, damage characterization for the studied finite element model was based on prior knowledge of the damage presented in the experimental test mentioned above. However, the type of damage can be defined by interpreting the stress-strain response of the numerical model components, taking into account the damage produced by the different failure mechanisms of the structures.
It is important to recognize that the numerical approach has taken into account some assumptions. For instance
Only a quarter of the full-size experimental setup was considered in the numerical model. This was possible due to the symmetry in geometry, boundary conditions, and applied loads. The symmetry conditions were implemented in the model by nodal displacement restrictions indicated in
Figure 6. We believe that this assumption has no impact on the final results and conclusions.
The constitutive models assumed for concrete and steel are a simplified representation of the real mechanical response. In general, more realistic and complex constitutive models for materials entail a higher degree of numerical complexity and hence major convergence difficulties. In this case, simpler constitutive models were used because contact and geometric nonlinearities were also accounted for.
Figure 8 shows that the predicted capability of the model fairs quite well when compared with the experimental data. Hence, the modeling assumptions do not seem to have a relevant impact on the global response of the structure.
The contact between both concrete and the steel elements was defined as frictionless. This assumption will lead to a lower interface stiffness that would be reflected in the global structural response. In fact, if we look at the results shown in
Figure 8, although the peak load is predicted quite well by the model, the numerical model presents a lower initial stiffness than the one obtained experimentally.
While the methodology employed in this study is effective for small to medium-scale structures, its scalability to larger systems may present certain challenges. One key limitation is the increased computational demand as the size and complexity of the structure grow. Larger structural systems involve a higher number of elements and degrees of freedom, which require significant computational resources. In addition, contact effects in large systems can introduce complexities that may not be captured accurately by the current modeling approach. In practical applications, challenges may be found in the availability and accuracy of input data. Detailed material properties, geometric data, and boundary conditions must be obtained with high precision, which can be difficult to obtain. Also, in situ testing and monitoring for large systems may require advanced equipment and logistics, which could complicate data collection and validation processes. To address these limitations, future work could focus on developing more efficient numerical techniques, such as reduced-order modeling or parallel computing, to handle the increased computational demands.
Further research and improvements of our approach will be conducted to achieve a more accurate classification of damage types. Therefore, a more extensive experimental study will be conducted to validate the proposed model under a wider range of loading conditions. Additionally, the integration of advanced machine learning techniques will be explored to further refine the damage prediction capabilities of our model.